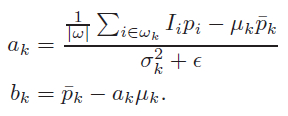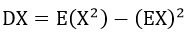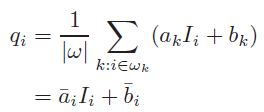上一篇文章已經說了引導濾波的基本理論，而且我們也知道引導濾波可以寫出時間複雜度與視窗大小無關的演算法，現在就來使用C++並藉助OpenCV實現這一演算法。

實現這種演算法的關鍵思想是盒式濾波（box filter），而且必須是通過積分圖來實現的盒式濾波，否則不可能與視窗大小無關，好在OpenCV的boxFilter函式滿足這個要求。

再看看引導濾波的公式

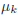
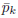
先計算a_k的分子，Ip 在視窗w_k中的和，再除以視窗中畫素的個數，剛好就是盒式濾波，因此我們可以將輸入的引導影象 I 和濾波影象 p 相乘，並對相乘後的影象做box filtering，即得第一項的結果。後面的和分別為 I 和 p 在視窗w_k中均值，因此分別對 I 和 p 進行box filtering，再將box filtering之後的結果相乘即可。實際上，a_k的分子就是 Ip 在視窗w_k中的協方差。

接下來計算a_k的分母部分。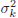是引導圖 I 在視窗w_k中的方差，學過概率論與數理統計的朋友應該知道，方差和期望（均值）之間是有關係的，如下式

因此在計算 I 的方差時，我們可以先計算 I*I 的均值，再減去 I 均值的平方即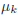的平方。在方法上，計算 I*I 的均值和計算 Ip 的均值是一樣的。最後，對計算出來的方差影象，加上常量e（每個元素都加e），分母就計算完了，自然，a_k在所有視窗中的值也就得到了。b_k的計算太簡單了，大家都懂的。

注意，我們的計算都是對整個影象的，以影象為單位進行計算，所以最後算出的也是兩張圖，a_k的圖（左邊）和b_k的圖（右邊），如下

在圖中可以看到，在邊緣部分或變化劇烈的部分，a的值接近於1（白色），b的值接近為0（黑色），而在變化平坦的區域，a的值接近0（黑色），b的值為平坦區域畫素的均值。這與

下面看第二個公式

輸出值q又與兩個均值有關，分別為a和b在視窗w_i中的均值（不是w_k），所以還是box filtering，我們將上一步得到兩個影象都進行盒式濾波，得到兩個新圖：a_i和b_i，然後用a_i乘以引導影象 I ，再加上b_i，即得最終濾波之後的輸出，如下（左邊為原圖，右邊為濾波之後的影象，其中濾波視窗半徑為8，e的值為500）：

下面是整個演算法的程式碼，僅供參考

void guidedFilter(Mat& source, Mat& guided_image, Mat& output, int radius, float epsilon)
{
	CV_Assert(radius >= 2 && epsilon > 0);
	CV_Assert(source.data != NULL && source.channels() == 1);
	CV_Assert(guided_image.channels() == 1);
	CV_Assert(source.rows == guided_image.rows && source.cols == guided_image.cols);

	Mat guided;
	if (guided_image.data == source.data)
	{
		//make a copy
		guided_image.copyTo(guided);
	}
	else
	{
		guided = guided_image;
	}

	//將輸入擴充套件為32位浮點型，以便以後做乘法
	Mat source_32f, guided_32f;
	makeDepth32f(source, source_32f);
	makeDepth32f(guided, guided_32f);

	//計算I*p和I*I
	Mat mat_Ip, mat_I2;
	multiply(guided_32f, source_32f, mat_Ip);
	multiply(guided_32f, guided_32f, mat_I2);

	//計算各種均值
	Mat mean_p, mean_I, mean_Ip, mean_I2;
	Size win_size(2*radius + 1, 2*radius + 1);
	boxFilter(source_32f, mean_p, CV_32F, win_size);
	boxFilter(guided_32f, mean_I, CV_32F, win_size);
	boxFilter(mat_Ip, mean_Ip, CV_32F, win_size);
	boxFilter(mat_I2, mean_I2, CV_32F, win_size);

	//計算Ip的協方差和I的方差
	Mat cov_Ip = mean_Ip - mean_I.mul(mean_p);
	Mat var_I = mean_I2 - mean_I.mul(mean_I);
	var_I += epsilon;

	//求a和b
	Mat a, b;
	divide(cov_Ip, var_I, a);
	b = mean_p - a.mul(mean_I);

	//對包含畫素i的所有a、b做平均
	Mat mean_a, mean_b;
	boxFilter(a, mean_a, CV_32F, win_size);
	boxFilter(b, mean_b, CV_32F, win_size);

	//計算輸出 (depth == CV_32F)
	output = mean_a.mul(guided_32f) + mean_b;
}
 

void makeDepth32f(Mat& source, Mat& output)
{
	if (source.depth() != CV_32F ) > FLT_EPSILON)
		source.convertTo(output, CV_32F);
	else
		output = source;
}