直接選擇排序到堆排序做的那些改進
1 你會學到什麼?
徹底弄明白常用的排序演算法的基本思想,演算法的時間和空間複雜度,以及如何選擇這些排序演算法,確定要解決的問題的最佳排序演算法,上個推送總結了氣泡排序和其改進後的快速排序這兩個演算法,下面總結直接選擇排序到堆排序的改進,後面再繼續總結插入排序、希爾排序、歸併排序和基數排序。
2 討論的問題是什麼?
各種排序演算法的基本思想;討論各種排序演算法的時間、空間複雜度;以及演算法的穩定性;演算法是如何改進的,比如氣泡排序如何改進成了目前最常用的快速排序的,直接選擇排序到堆排序的改進,正是接下來要討論的物件。
3 相關的概念和理論
內部排序
若整個排序過程不需要訪問外存便能完成,則稱此類排序問題為內部排序。
外部排序
若參加排序的記錄數量很大,整個序列的排序過程不可能在記憶體中完成,則稱此類排序問題為外部排序。
就地排序
若排序演算法所需的輔助空間並不依賴於問題的規模n,即輔助空間為O(1),稱為就地排序。
穩定排序
假定在待排序的記錄序列中,存在多個具有相同的關鍵字的記錄,若經過排序後,這些記錄的相對次序保持不變,即在原序列中 ri=rj, ri 在 rj 之前,而在排序後的序列中,ri 仍在 rj 之前,則稱這種排序演算法是穩定的;否則稱為不穩定的。
排序序列分佈
排序需要考慮待排序關鍵字的分佈情況,這會影響對排序演算法的選擇,通常我們在分析下列演算法時都考慮關鍵字分佈是隨機分佈的,不是按照某種規律分佈的,比如正態分佈等。
待排序序列
排序序列中,剩餘即將要排序的序列部分。
已排序序列
排序序列中,已經排序好的序列部分。
4 直接選擇排序
直接選擇排序,英文名稱 :Straight Select Sorting,是一個直接從未排序序列選擇最值到已排序序列的過程。
基本思想
第一次從R[0]~R[n-1]中選取最小值,與R[0]交換;
第二次從R[1]~R[n-1]中選取最小值,與R[1]交換,….,
第 i 次從R[i-1]~R[n-1]中選取最小值,與R[i-1]交換,…..,
總共通過n-1次,得到一個按關鍵碼從小到大排列的有序序列。
升序排序的例子
我們仍然用上節氣泡排序和快速排序舉的例子。待排序列
3 2 5 9 2
演示如何用直接選擇排序得到升序序列。
第一輪,從所有關鍵碼中選擇最小值與 R[0]交換,3與2交換,如下圖所示,
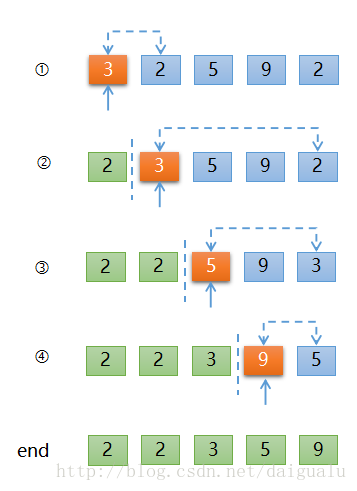
第二輪,從 R[1]~R[n-1]中選擇最小值與R[1]交換,3與2交換;
第三輪,從 R[2]~R[n-1]中選擇最小值與R[2]交換,5與3交換;
第四輪,從 R[3]~R[n-1]中選擇最小值與R[3]交換,9與5交換;
終止。
演算法評價
在直接選擇排序中,共需要進行 n-1 輪,每輪必發生一次交換,每輪需要進行 n-i 次比較 (1<=i<=n-1),總的比較次數等於
(n-1) + (n-2) + … + ( n-(n-1) )
化簡後等於 n + (n-1)(n-2)/2
由此可知,直接選擇排序的時間複雜度為 O(n^2) ,空間複雜度為 O(1) 。注意到,直接選擇排序在最好和最壞情況下都是 O(n^2) 。
一般地,排序演算法的時間複雜度為 O(n^2)是不令人滿意的排序演算法,在選擇排序演算法的思想下,有一種選擇排序演算法提升了時間效能,它就是堆排序,接下來我們就看下堆排序。
5 直接選擇的優化版之堆排序
堆排序,英文名稱 Heapsort,利用二叉樹(堆)這種資料結構所設計的一種排序演算法,是一種對直接選擇排序的一種改建演算法。在邏輯結構上是按照二叉樹儲存結構,正是這種結構優化了選擇排序的效能,在物理儲存上是連續的陣列儲存,它利用了陣列的特點快速定位指定索引的元素。這麼巧妙的演算法又是哪位科學家發明的呢?
自學成才的電腦科學家 Flody
這個演算法是計算機先驅獎獲得者、斯坦福大學計算機科學系教授羅伯特·弗洛伊德(Robert W.Floyd)和威廉姆斯(J.Williams)在1964年共同發明的堆排序演算法,我們認識下弗洛伊德。

沒錯,就是這位,第一眼看上去是搞藝術創作的,沒錯他的確是在芝加哥大學讀的文學,後來因為苦於找不上工作,改行去西屋電氣公司當了二年計算機操作員,發現他對計算機非常感興趣。
於是他下定決心要弄懂它,掌握它,於是他借了有關書籍資料在值班空閒時間刻苦學習鑽研,有問題就虛心向程式設計師請教。白天不值班,他又回校去聽講有關課程,逐漸從計算機的門外漢變成計算機的行家裡手。
1956年他離開西屋電氣公司,到芝加哥的裝甲研究基金會(Armour Research Foundation),開始還是當操作員,後來就當了程式設計師。1962年他被馬薩諸塞州的Computer Associates公司聘為分析員。1965年他應聘成為卡內基—梅隆大學的副教授,3年後轉至斯坦福大學,1970年被聘任為教授。
之所以能這樣快地步步高昇,關鍵就在於弗洛伊德通過勤奮學習和深入研究,是一位自學成才的電腦科學家。
堆排序的基本概念
n個關鍵字序列 Kl,K2,…,Kn 稱為堆(Heap),當且僅當該序列滿足如下性質:
Ki <= K( 2i + 1 )且 Ki <= K( 2i + 2 ) ( 0≤i≤ (n/2)-1),稱為小根堆;
Ki >= K( 2i + 1) 且 Ki >= K( 2i +2 ) ( 1≤i≤ (n/2)-1), 稱為大根堆。
堆排序的演算法思想
堆分為大根堆和小根堆,是完全二叉樹。大根堆的要求是每個節點的值都不大於其父節點的值,即 R[PARENT[i]] >= R[i]。在陣列的非降序排序中,需要使用的就是大根堆,因為根據大根堆的要求可知,最大的值一定在堆頂。小根堆與之類似,每個節點的值都不小於父節點的值,最小值出現在樹根處。
堆排序利用了大根堆(或小根堆)堆頂記錄的關鍵字最大(或最小)這一特徵,使得在當前無序區中選取最大(或最小)關鍵字的記錄變得簡單。
堆排序是如何工作的
以大根堆排序為例,即要得到非降序序列。
- 先將初始檔案R[0..n-1]建成一個大根堆,此堆為初始的無序區。
- 再將關鍵字最大的記錄R[0](即堆頂)和無序區的最後一個記錄R[n-1]交換,由此得到新的無序區 R[0..n-2] 和有序區 R[n-1],且滿足 R[0..n-2] ≤ R[n-1]
由於交換後新的根R[0]可能違反堆性質,故應將當前無序區R[0..n-2]調整為堆。然後再次將R[0..n-2]中關鍵字最大的記錄R[0]和該區間的最後一個記錄R[n-2]交換,由此得到新的無序區R[0..n-3] 和 有序區R[n-2..n-1],且仍滿足關係R[0..n-3] ≤ R[n-2..n-1]。 - 重複步驟2和步驟3,直到無序區只有一個元素為止。
堆排序演算法涉及到的兩個主要操作正如上演算法所描寫的那樣,先構建一個初始堆,然後堆頂不斷地和當前無序區的最後一個元素交換,交換可能會導致初始構建的大根堆不再是大根堆,所以需要再次調整堆(這個實際上還是構建一個初始堆的函式),簡單來說:
構建堆
- 交換堆頂和無序區的最後一個元素,再次構建大根堆;
- 重複步驟2的操作,直至無序區只剩下一個元素為止。
應用堆排序得到升序排序的例子
我們仍然用那個待排序列
3 2 5 9 2
第一步,我們需要構建大根堆,為了構建大根堆,我們再溫習下剛才的堆排序的基礎知識,首先以上待排序列的物理儲存結構和邏輯儲存結構的示意圖如下所示,
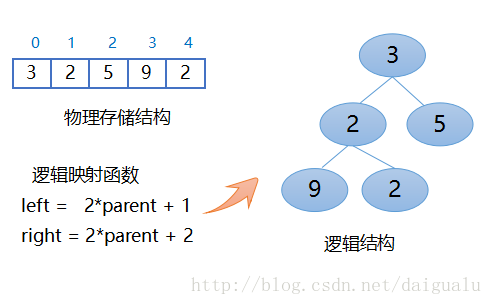
構建初始堆是從length/2 - 1,即從索引1處關鍵碼等於2開始構建,2的左右孩子等於9, 2,它們三個比較後,父節點2與左孩子9交換,如下圖所示:
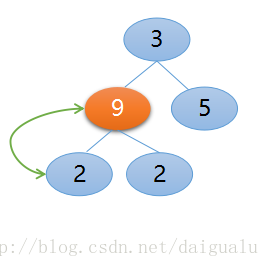
接下來從索引1減1等於0處,即元素3開始與其左右孩子比較,比較後父節點3與左孩子節點9交換,如下所示:
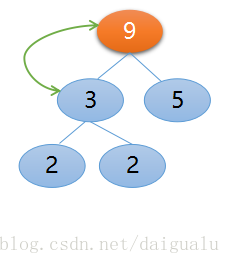
因為索引等於 0 了,所以構建堆結束,得到大根堆,第一步工作結束,下面開始第二步調整堆,也就是不斷地交換堆頂節點和未排序區的最後一個元素,然後再構建大根堆,下面開始這步操作,交換棧頂元素9(如上圖所示)和未排序區的最後一個元素2,如下圖所示,現在排序區9成為了第一個歸位的,
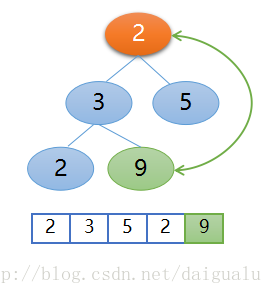
接下來拿掉元素9,未排序區變成了2,3,5,2,然後從堆頂2開始進行堆的再構建,比較父節點2與左右子節點3和5,父節點2和右孩子5交換位置,如下圖所示,這樣就再次得到了大根堆,
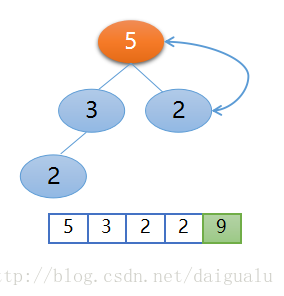
再交換堆頂5和未排序區的最後一個元素2,這樣5又就位了,這樣未排序區變為了2,3,2,已排序區為 5,9,交換後的位置又破壞了大根堆,已經不再是大根堆了,如下圖所示,
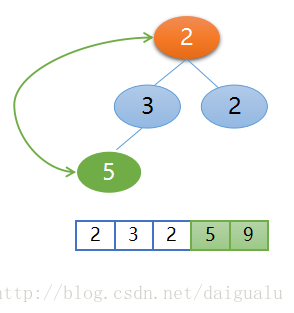
所以需要再次調整,然後堆頂2和左孩子3交換,交換後的位置如下圖所示,這樣二叉樹又重新變為了大根堆,再把堆頂3和此時最後一個元素也就是右孩子2交換,
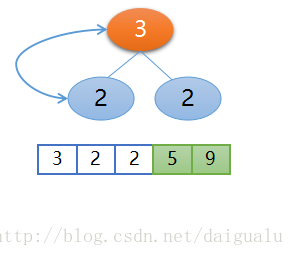
接下來再構建堆,不再贅述,見下圖,
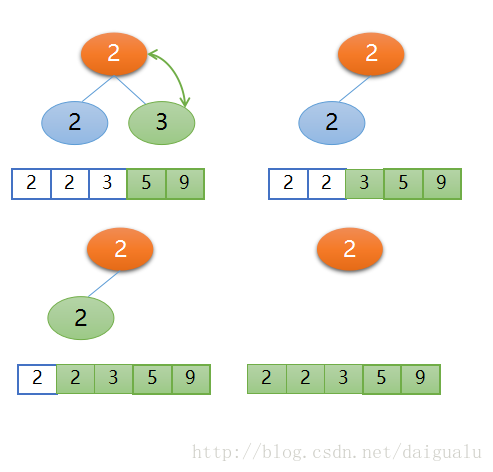
演算法評價
堆排序的時間,主要由建立初始堆和反覆重建堆這兩部分的時間開銷構成,堆排序的平均時間複雜度是O(nlogn) 。堆排序是就地排序,空間複雜度為O(1)。
通過上面的例子,可以看到兩個關鍵碼2的相對位置會發生變化,所以堆排序是不穩定的排序方法。
由於建初始堆所需的比較次數較多,所以堆排序不適宜於記錄數較少的檔案。
6 總結
直接排序演算法是時間複雜度為O(n^2)的不穩定排序演算法,為了改進它的時間複雜度,flody等人藉助二叉樹的形,巧妙地選擇最值,通過堆這種邏輯結構,將時間複雜度提升到了O(nlogn)。
因此,同樣是選擇排序的演算法,直接選擇和堆選擇時間差別還是不小,但是堆排序演算法不大適宜資料量較少的情況,因為光構建初始堆就要進行很多次比較。
接下來,總結插入演算法涉及的直接插入排序和希爾排序,加油!
歡迎關注《演算法思考與應用》公眾號

