平臺：windows10 64位
IDE：Pycharm
Python版本：Python3.5
github程式碼：原始碼

1 目錄

2 迴歸的理解

迴歸是由高爾頓最先在生物遺傳上提出的，線上性迴歸中，與其說其為迴歸，不如說線性擬合更合適，而為了紀念高爾頓還是保留了迴歸這一名詞
而對數機率迴歸（Logistic regression）解決的卻是一個分類問題，其實就是2分類，如果需要解決多分類那麼就做多次2分類或直接用Softmax迴歸。

3 線性迴歸

線性迴歸試圖建立的一個線性模型以儘可能準確的預測輸出標記。考慮最簡單的模型，給定若干對(x,y)$(x,y)$的資料，將其在座標軸上表示如下：

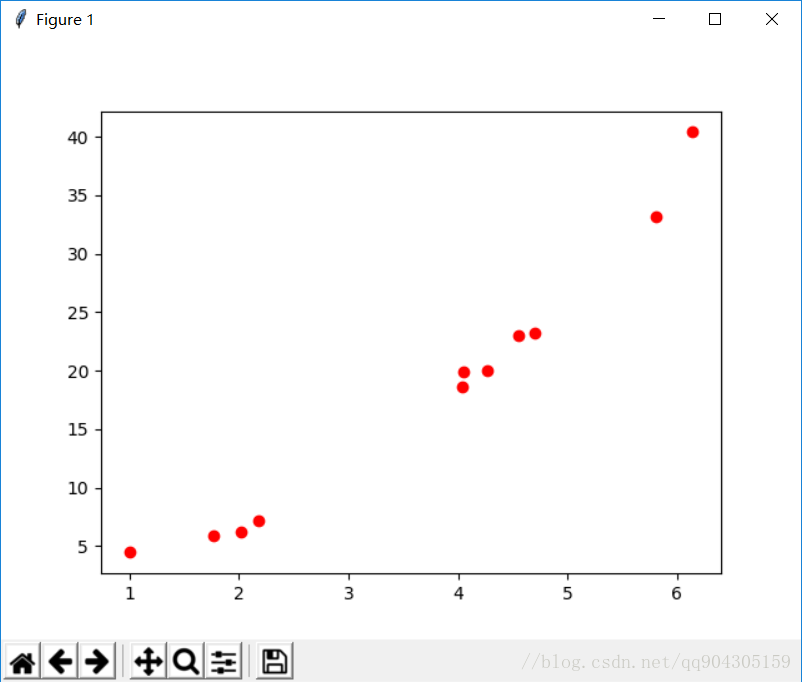
線性迴歸就是要尋找一條直線來使得這些所有的點都儘量符合直線上的點，其中儘量符合指的就是使損失最小，在這裡以點到直線的距離的平方來作為‘損失’，使用線性迴歸可以來預測資料，這在機器學習裡面是一個非常重要的概念——預測，不管是什麼模型，最後做出來都是需要用來預測資料，來判斷這個模型到底實不實用，線性迴歸就是這些模型中最簡單的一種模型。

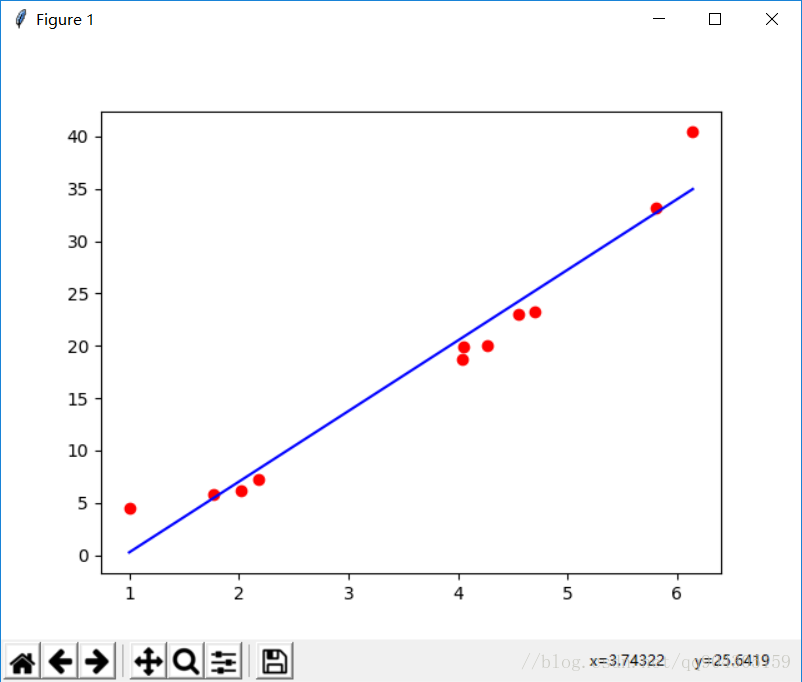
4 使用最大似然解釋最小二乘

4.1 基本形式

首先對於線性迴歸，所求得就是一條直線，設其方程為：

y(i)=θTx(i)+ε(i)$$y^{(i)}={\theta }^T{x}^{(i)}+{\epsilon }^{(i)}$$
其中θ$\theta$和ε$\epsilon$為這條直線的斜率和截距，x,y$x,y$分別為圖上的一系列散點，用極大似然法估計時，我們認為

ε$\epsilon$符合正太分佈，且期望為0，那麼根據大學的知識可以得到ε$\epsilon$的概率為：
p(ε(i))=1s2πσ−−−√exp(−(ε(i))22σ2)$$p({\epsilon }^{(i)})=\frac{1}{s\sqrt{2\pi \sigma }}exp(-\frac{({\epsilon }^{(i)}{)}^2}{2{\sigma }^2})$$
把直線方程移項帶入上式得到在θ$\theta$引數下，已知x$x$的情況下y$y$的概率密度函式為：
p(y(i)|x(i);θ)=12πσ−−−√exp(−(y(i)−θTx(i))22σ2)$$p(y^{(i)}|x^{(i)};\theta )=\frac{1}{\sqrt{2\pi \sigma }}exp(-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2})$$
這裡的概率密度函式為條件概率密度函式，直接求解是無法解出來的，假設樣本之間是獨立的，那麼就得到： L(θ)=∐i=1mp(y(i)|

x(i);θ)=∐i=1m12πσ−−−√exp(−(y(i)−θTx(i))22σ2)$$\begin{array}{rl}L(\theta )& =\coprod _{i=1}^{m}p(y^{(i)}|x^{(i)};\theta )\\ =\coprod _{i=1}^m\frac{1}{\sqrt{2\pi \sigma }}exp(-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2})\end{array}$$

4.2 高斯的對數似然與最小二乘

這裡用的是對數似然，即需要對L(θ)$L(\theta )$取對數，則可以化簡得到如下方程：

ℓ(θ)

相關推薦

機器學習之線性迴歸筆記

平臺：windows10 64位 IDE：Pycharm Python版本：Python3.5 github程式碼：原始碼 1 目錄 2 迴歸的理解 迴歸是由高爾頓最先在生物遺傳上提出的，線上性迴歸中，與其說其為迴歸，不如說線性擬合更合

機器學習之線性迴歸-AndrewNg學習筆記

監督學習 從討論監督學習問題的例子出發，假設我們有某個地區住房面積和相應房價的資料集合。對於這樣的給定的資料， 我們的目的是要利用已有的資訊，來對房價建立預測模型。即對於給定的房屋資訊(房屋面積)預測其房價。 把這些資料在圖上表示： 為了方便以後的使用，我們首先定義一些

JavaScript機器學習之線性迴歸

譯者按: AI時代，不會機器學習的JavaScript開發者不是好的前端工程師。 原文: Machine Learning with JavaScript : Part 1 譯者: Fundebug 為了保證可讀性，本文采用意譯而非直譯。另外，本文版權歸原作者所有，翻譯僅用於學習。

【ML2】機器學習之線性迴歸

【知識儲備】 線性迴歸： 1： 函式模型（Model）： 假設有訓練資料   那麼為了方便我們寫成矩陣的形式   2： 損失函式（cost）：  現在我們需要根據給定的X求解W的值，這裡採用最小二乘法。   

機器學習之線性迴歸SVR

機器學習之線性迴歸SVR # -*- coding: utf-8 -*- """ Created on Sun Dec 2 09:53:01 2018 @author: muli """ import matplotlib.pyplot as plt import

機器學習之線性迴歸（Linear Regression）

線性學習中最基礎的迴歸之一，本文從線性迴歸的數學假設，公式推導，模型演算法以及實際程式碼執行幾方面對這一回歸進行全面的剖析~ 一：線性迴歸的數學假設 1.假設輸入的X和Y是線性關係，預測的y與X通過線性方程建立機器學習模型 2.輸入的Y和X之間滿足方程Y= θ

機器學習之線性迴歸原理及sklearn實現

  1、線性迴歸問題        以房價預測為例，佔地面積為變數x1，房屋年齡為變數x2，房屋價格為預測變數y。        為什麼叫線性迴歸問題，因為目標函式是一個線性迴歸函式。什麼是目標函式？        （1）、目標函式：目標函式是我們需要的最終結果，及

機器學習之線性迴歸演算法(Linear Regression)(含python原始碼)

機器學習之線性迴歸演算法(Linear Regression) 線性迴歸(Linear Regression)演算法屬於有監督的迴歸(Regression)學習演算法。迴歸(Regression)演算法通過建立變數之間的迴歸模型，通過學習(訓練)過程得到變數與

機器學習之線性迴歸極大似然估計法

leboop文章，禁止轉載！ 請閱讀《機器學習之矩陣微積分及其性質》和《機器學習之線性迴歸公式推導》。首先我們還是使用如下的資料：   feature_1 feature_2   feature_n

機器學習之線性迴歸公式推導

leboop文章，禁止轉載！ 本文所有符號約定參見機器學習之矩陣微積分及其性質。 假設我們獲得了個數據，每一個數據由個特徵和一個真實值構成，如下：   feature_1 feature_2   fe

機器學習之線性迴歸模型

當我們拿到樣本並經過特徵降維後得到 x1、x2 … 低維特徵，經過多項式對映得到線性迴歸的模型假設： 上式 x1、x2 是樣本特徵，如果 y 是現實中房子的價格，那麼 x1、x2 相當於房子的面積、臥室數量等影響房子價格的因素，而 θ0、θ1、θ2 … 是係數

機器學習之線性迴歸及程式碼示例

一、線性迴歸 線性迴歸一般用來做連續值的預測，預測的結果為一個連續值。因訓練時學習樣本不僅要提供學習的特徵向量X，而且還要提供樣本的實際結果（標記label），所以它是一種有監督學習。其中 X={x0,x1,...,xn}。 線性迴歸需要學習得到的是一個對映

機器學習之線性迴歸：演算法兌現為python程式碼

前面三天推送機器學習線性迴歸演算法之最小二乘法，從假設到原理，詳細分析了直接求解和梯度下降兩種演算法，接下來手動編寫python程式碼實現線性迴歸的演算法吧。 1 資料預處理 在拿到一個數據集後，往往需要經過漫長的預處理過程，不要忽視這個看似與建立模

機器學習之線性迴歸（機器學習基石）

引子 在一個二元分類的問題中我們通常得到的結果是1/0，而在分類的過程中我們會先計算一個得分函式然後在減去一個門檻值後判斷它的正負若為正則結果為1若為負結果為0。 事實上從某種角度來看線性迴歸只是二元分類步驟中的一個擷取它沒有後面取正負號的操作，它的輸出結果為一個實數而非

spark Ml 機器學習之 線性迴歸

本文版本選自spark 2.1.0寫這篇文章之前已閱讀過官網api，演算法本身自認為自己手動寫，應該可以搞定（進一步優化不提）；但是官網卻看的我迷迷糊糊的，引數選擇和結果獲取，描述不夠清晰，寫這篇文字的目的就是為了理清所有官網沒有解答的謎團；演算法本身比較簡單，網上文章也很多

機器學習之線性迴歸

目錄 線性迴歸 模型表示 模型評估 模型學習 模型總結 演算法流程 存在的問題 演算法優化 線性迴歸 輸出是一個連續的數值。 模型表示 對於一個目標值，它可能受到多個特徵的加權影響。例如寶可夢精靈的進化的 cp 值，它不僅受到進化前的 cp 值的影響，還可能與寶可夢的 hp 值、型別、高度以及重量

20171028機器學習之線性回歸過擬合問題的解決方案

ces 函數 彈性 alpha mach rom 定性 ast cep 在函數中加入一個正則項： 三種方式： 一、Ridge回歸（嶺回歸）： 　　優點：具有較高的準確性、魯棒性以及穩定性 　　缺點：求解速度慢 二、Lasso回歸： 　　優點：求解速度快（原理降維計算

機器學習入門 線性迴歸及梯度下降

分享一下我老師大神的人工智慧教程！零基礎，通俗易懂！http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識，造福人民，實現我們中華民族偉大復興！        

機器學習實現——線性迴歸

線性迴歸，作為機器學習入門，比較好理解，小學數學中y=kx+b到研究生階段開始進行了深度研究，之前用兩對引數確定兩個未知數，現在用n對引數來估計一套近似值，不過由於未知數的數量，以及線性模型的不確定，要讓線性迴歸達到一個預測未來還是相當有難度的。隨著一些重要的模型和深度學習的引入，線性迴歸雖

機器學習演算法 - 線性迴歸

線性迴歸演算法 解決迴歸問題 思想簡單，容易實現 許多強大的非線性模型的基礎 結果具有很好的可解釋性 蘊含機器學習中很多重要的思想$$y=ax_i +b$$   樣本特徵只有一個的線性迴歸問題，為簡單線性迴歸。 樣本特徵有多個的線性迴歸問題