一、線性迴歸

線性迴歸一般用來做連續值的預測，預測的結果為一個連續值。因訓練時學習樣本不僅要提供學習的特徵向量X，而且還要提供樣本的實際結果（標記label），所以它是一種有監督學習。其中 X={x0,x1,...,xn}。

線性迴歸需要學習得到的是一個對映關係 f：X→y，即當給定新的待預測樣本時，我們可以通過這個對映關係得到一個測試樣本 X 的預測值 y 。

線上性迴歸中，假定輸入X和輸出y之間具有線性相關的關係。
例如當特徵向量 X 中只有一個特徵時，需要學習到的函式應該是一個一元線性函式 y=a+bx。

當情況複雜時，考慮 X 存在n個特徵的情形下，我們往往需要得到更多地係數。我們將 X

到 y 的對映函式記作函式hθ(X)：

hθ(X)=∑i=0nθixi=θTX

其中，為了在對映函式hΘ(X)中保留常數項，令 x0 為1，所以特徵向量X={1,x1,x2,...,xn}，特徵係數向量 θ={θ0,θ1,θ2,...,θn} 。

當給定一個訓練集資料的情況，可以通過某個演算法，學習出來一個線性的對映函式 hθ(X) 來求得預測值 y。

二、損失函式

在需要通過學習得到的對映函式 hθ(X) 中，需要通過訓練集得到特徵係數向量 θ={θ0,θ1,θ2,...,θn} 。

那怎麼得到所需的特徵係數向量？怎麼保證得到的特徵係數向量是足夠好？這裡會有一個評判標準：損失函式。

根據特徵向量係數 θ，可有損失函式 J(θ) 如下 :

J(θ)=12m∑i=1m(hθ(X(i))−y(i))2

其中 hθ(X) 為需要學習到的函式，m 為訓練集樣本的個數，Xi 表示訓練集中第 i 個樣本的特徵向量，yi 表示第 i 個樣本中的標籤。

為了得到預測值 hθ(Xi) 和 yi 的絕對值，在公式上使用了平方數。為了平均每個樣本的損失，在公式上對損失和進行除以 m 操作，，再除以 2 是為了之後的求導計算。

三、梯度下降演算法求解

批量隨機梯度下降BGD

在上面，找到了一個特徵係數向量 θ 好壞的損失函式 J(θ)。為了迎合這樣的評判標準得到較好的 θ

，需對損失函式值進行最小化，即讓損失函式在樣本中的損失最小。

對於損失函式 J(θ)，可以發現 θ 是一個關於 \theta 的凸函式。

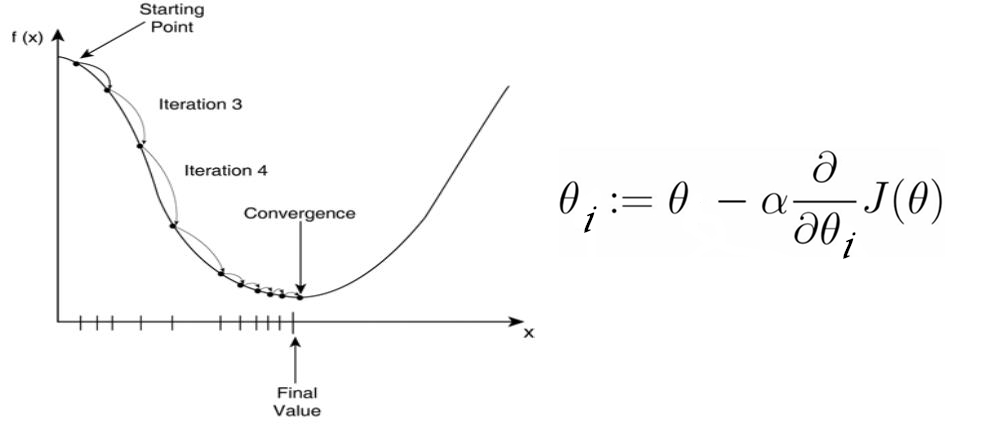
梯度下降就是一個不斷地最小化損失函式的過程。從影象上來看，先初始化 θi 為某個值，然後讓 θi 沿著J J(θ) 在 θi 的偏導方向不斷地走，直達走到底部收斂為止，最後就可以得到 J(θ) 最小時的那個 θi 的值。

這個不斷迭代的過程猶如一個不斷下山的過程，我們可以得到圖中關於 θi 的迭代函式，其中 α 為每次下山的步長。

當 θi 小於最低處的值的時，對其的偏導為負，在迭代過程中， θi 不斷地增大以逼近最低處的值；當 θi 大於最低處的值時，對其的偏導為正， θi 會不斷地做減法以逼近最低處的值。所以當步長 α 較小時， θi 會收斂於最低處的值。通常，我們將

相關推薦

機器學習之線性迴歸及程式碼示例

一、線性迴歸 線性迴歸一般用來做連續值的預測，預測的結果為一個連續值。因訓練時學習樣本不僅要提供學習的特徵向量X，而且還要提供樣本的實際結果（標記label），所以它是一種有監督學習。其中 X={x0,x1,...,xn}。 線性迴歸需要學習得到的是一個對映

機器學習之線性迴歸原理及sklearn實現

  1、線性迴歸問題        以房價預測為例，佔地面積為變數x1，房屋年齡為變數x2，房屋價格為預測變數y。        為什麼叫線性迴歸問題，因為目標函式是一個線性迴歸函式。什麼是目標函式？        （1）、目標函式：目標函式是我們需要的最終結果，及

機器學習之線性迴歸：演算法兌現為python程式碼

前面三天推送機器學習線性迴歸演算法之最小二乘法，從假設到原理，詳細分析了直接求解和梯度下降兩種演算法，接下來手動編寫python程式碼實現線性迴歸的演算法吧。 1 資料預處理 在拿到一個數據集後，往往需要經過漫長的預處理過程，不要忽視這個看似與建立模

機器學習入門 線性迴歸及梯度下降

分享一下我老師大神的人工智慧教程！零基礎，通俗易懂！http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識，造福人民，實現我們中華民族偉大復興！        

JavaScript機器學習之線性迴歸

譯者按: AI時代，不會機器學習的JavaScript開發者不是好的前端工程師。 原文: Machine Learning with JavaScript : Part 1 譯者: Fundebug 為了保證可讀性，本文采用意譯而非直譯。另外，本文版權歸原作者所有，翻譯僅用於學習。

【ML2】機器學習之線性迴歸

【知識儲備】 線性迴歸： 1： 函式模型（Model）： 假設有訓練資料   那麼為了方便我們寫成矩陣的形式   2： 損失函式（cost）：  現在我們需要根據給定的X求解W的值，這裡採用最小二乘法。   

機器學習之線性迴歸SVR

機器學習之線性迴歸SVR # -*- coding: utf-8 -*- """ Created on Sun Dec 2 09:53:01 2018 @author: muli """ import matplotlib.pyplot as plt import

機器學習之線性迴歸（Linear Regression）

線性學習中最基礎的迴歸之一，本文從線性迴歸的數學假設，公式推導，模型演算法以及實際程式碼執行幾方面對這一回歸進行全面的剖析~ 一：線性迴歸的數學假設 1.假設輸入的X和Y是線性關係，預測的y與X通過線性方程建立機器學習模型 2.輸入的Y和X之間滿足方程Y= θ

機器學習之線性迴歸演算法(Linear Regression)(含python原始碼)

機器學習之線性迴歸演算法(Linear Regression) 線性迴歸(Linear Regression)演算法屬於有監督的迴歸(Regression)學習演算法。迴歸(Regression)演算法通過建立變數之間的迴歸模型，通過學習(訓練)過程得到變數與

機器學習之線性迴歸極大似然估計法

leboop文章，禁止轉載！ 請閱讀《機器學習之矩陣微積分及其性質》和《機器學習之線性迴歸公式推導》。首先我們還是使用如下的資料：   feature_1 feature_2   feature_n

機器學習之線性迴歸公式推導

leboop文章，禁止轉載！ 本文所有符號約定參見機器學習之矩陣微積分及其性質。 假設我們獲得了個數據，每一個數據由個特徵和一個真實值構成，如下：   feature_1 feature_2   fe

機器學習之線性迴歸模型

當我們拿到樣本並經過特徵降維後得到 x1、x2 … 低維特徵，經過多項式對映得到線性迴歸的模型假設： 上式 x1、x2 是樣本特徵，如果 y 是現實中房子的價格，那麼 x1、x2 相當於房子的面積、臥室數量等影響房子價格的因素，而 θ0、θ1、θ2 … 是係數

機器學習之線性迴歸筆記

平臺：windows10 64位 IDE：Pycharm Python版本：Python3.5 github程式碼：原始碼 1 目錄 2 迴歸的理解 迴歸是由高爾頓最先在生物遺傳上提出的，線上性迴歸中，與其說其為迴歸，不如說線性擬合更合

機器學習之線性迴歸（機器學習基石）

引子 在一個二元分類的問題中我們通常得到的結果是1/0，而在分類的過程中我們會先計算一個得分函式然後在減去一個門檻值後判斷它的正負若為正則結果為1若為負結果為0。 事實上從某種角度來看線性迴歸只是二元分類步驟中的一個擷取它沒有後面取正負號的操作，它的輸出結果為一個實數而非

機器學習之線性迴歸-AndrewNg學習筆記

監督學習 從討論監督學習問題的例子出發，假設我們有某個地區住房面積和相應房價的資料集合。對於這樣的給定的資料， 我們的目的是要利用已有的資訊，來對房價建立預測模型。即對於給定的房屋資訊(房屋面積)預測其房價。 把這些資料在圖上表示： 為了方便以後的使用，我們首先定義一些

spark Ml 機器學習之 線性迴歸

本文版本選自spark 2.1.0寫這篇文章之前已閱讀過官網api，演算法本身自認為自己手動寫，應該可以搞定（進一步優化不提）；但是官網卻看的我迷迷糊糊的，引數選擇和結果獲取，描述不夠清晰，寫這篇文字的目的就是為了理清所有官網沒有解答的謎團；演算法本身比較簡單，網上文章也很多

機器學習之線性迴歸

目錄 線性迴歸 模型表示 模型評估 模型學習 模型總結 演算法流程 存在的問題 演算法優化 線性迴歸 輸出是一個連續的數值。 模型表示 對於一個目標值，它可能受到多個特徵的加權影響。例如寶可夢精靈的進化的 cp 值，它不僅受到進化前的 cp 值的影響，還可能與寶可夢的 hp 值、型別、高度以及重量

機器學習（一）邏輯迴歸與softmax迴歸及程式碼示例

本文適合已經對機器學習、人工智慧有過一定了解，但是還沒有自己寫過程式碼，或者一直在使用現有框架的同學。不用框架自己寫一次程式碼的過程還是很有必要的，能讓你真正地理解原理與機器學習中各個步驟的實現過程，而不是停留在“好像懂了”、只會調庫的階段。 目錄

機器學習之logistic迴歸演算法與程式碼實現

                                       Logistic迴歸演算法與程式

ML-64: 機器學習之線性判別分析(Linear Discriminant Analysis)降維演算法+程式碼

線性判別分析(Linear Discriminant Analysis)降維演算法 機器學習分為監督學習、無監督學習和半監督學習(強化學習)。無監督學習最常應用的場景是聚類(clustering)和降維(dimension reduction)。聚類演算法包括