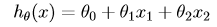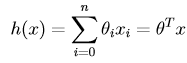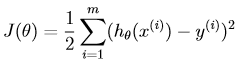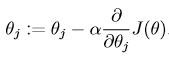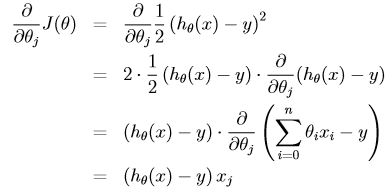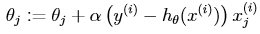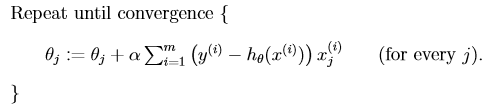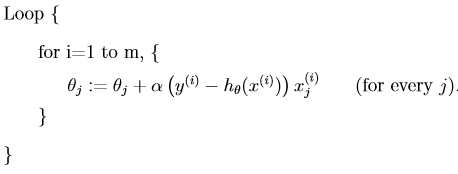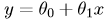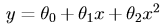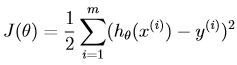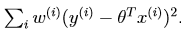機器學習之線性迴歸-AndrewNg學習筆記
監督學習
從討論監督學習問題的例子出發,假設我們有某個地區住房面積和相應房價的資料集合。對於這樣的給定的資料, 我們的目的是要利用已有的資訊,來對房價建立預測模型。即對於給定的房屋資訊(房屋面積)預測其房價。
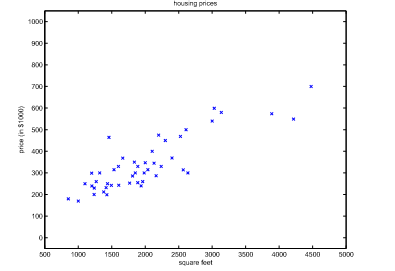
把這些資料在圖上表示:
為了方便以後的使用,我們首先定義一些符號標記。我們使用x(i)表示輸入變數(或者是特徵),使用y(i)表示我們將要預測的輸出變數或者說是目標變數(或者叫做標記)。(x(i), y(i))被稱作是一個訓練樣本,訓練樣本的集合稱作訓練集。
在這裡給出監督學習的比較正式的定義:對於給定的訓練集,我們的目標是要學習到函式h,使得h(x)能夠儘量準確的預測目標變數y。
當所要預測的目標變數y是連續的時候,這類學習問題為迴歸問題。當y僅僅能取一些離散值時稱之為分類問題。
線性迴歸
假設收集到的有關房價的資料如下(增加了一個特徵:臥室的個數):
為了執行監督學習演算法,首先要決定的是如何在計算機中表示假設函式h。在這裡我們決定把房價表示為特徵的線性函式:
其中θ為引數(或者可以理解為權重),依照慣例,x0 = 1,可以得到向量表示的形式:
其中n是特徵的個數。
現在對於給定的訓練集合,問題是我們要如何選取(學習)引數θ。一個合理的想法是使得h(x)的值儘量逼近真實標記y(起碼在給定的訓練集合上努力做到這一點)。我們定義如下的代價函式(它描述的是在任一θ下,h(x)和相應的y的接近程度),代價函式如下:(那麼現在我們的目標就是要使得如下的cost function的值最小)
LMS演算法:
我們的目標是找到使得J(θ)最小的引數向量θ,為了達到這樣的目的,我們需要使用一種搜尋演算法:給定初始的θ值,並且不斷改變θ的值是的J(θ)更小直到θ收斂。在這裡我們使用的梯度下降演算法:從初始的θ值開始按照以下的形式不斷更新:
(note:對所有的θ要同時更新)。alpha稱為學習速率或者步長。這個演算法的基本思想是:要選擇θ使得J(θ)達到最小,那麼我每次沿著使J下降最快的方向走一步,而這個下降最快的方向就是梯度的方向。接下來是要進行偏導的求解。首先考慮只有一個樣本的情況:
那麼對於單個數據樣本,我們得到的更新規則如下:
將上式稱為LMS(least mean squares)更新規則。將其推廣到多個樣本的情形得到以下的求解方法:
這就是原始的代價函式的梯度下降演算法。需要注意的是:該演算法在更新每一個θ時,都要遍歷整個訓練集。所以該演算法也叫做批梯度下降演算法。(需要說明的是,儘管梯度下降演算法一般會受到區域性最小值的影響,但我們在求解線性迴歸時做面臨的最優化問題僅有一個全域性最優解)。
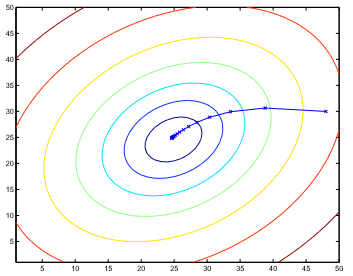
上圖是一個二次函式的等高線示意圖,同時也表明了梯度下降從初始值(48,30)的計算軌跡,圖中由直線連起來的X表明了θ的梯度下降軌跡。
梯度下降演算法的C語言程式碼實現(輸入資料並不是大神吳恩達所用的資料,因為沒有下載到)
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<string.h>
int feature_size;
int data_size;
char filename[20];
double** feature;
double* theta;
double* theta_new;
void readData();
void gradientDescent();
int main(int argc, char** argv)
{
if( argc != 4 )
{
printf("1.feature_size:\n"
"2.data_size\n"
"3.filename\n");
exit(0);
}
feature_size = atoi(argv[1]);
data_size = atoi(argv[2]);
strcat(filename, argv[3]);
printf("%d,%d,%s\n", feature_size, data_size,filename);
readData();
gradientDescent();
return 0;
}
void readData()
{
FILE* fread;
if( NULL == (fread = fopen(filename,"r")) )
{
printf("open file error");
exit(0);
}
if( !(feature = (double**)malloc(sizeof(double*) * data_size)) )
{
printf("feature** malloc error");
exit(0);
}
int i;
for( i = 0; i < data_size; i++ )
{
if( !(feature[i] = (double*)malloc(sizeof(double) * (feature_size + 2))) )
{
printf("feature[%d]* malloc error", i);
exit(0);
}
}
int j;
for( i = 0; i < data_size; i++ )
{
feature[i][0] = 1.0;
for( j = 1; j <= feature_size + 1; j++ )
{
if( 1 != fscanf(fread, " %lf ", &feature[i][j]) )
{
printf("fscanf error %d %d", i, j);
exit(0);
}
}
}
for( i = 0; i < data_size; i++ )
{
for( j = 0; j <= feature_size + 1; j++ )
{
printf("%lf\t", feature[i][j]);
}
printf("\n");
}
}
void gradientDescent()
{
if( !(theta = (double*)malloc(sizeof(double) * (feature_size + 1))) )
{
printf("theta* malloc error");
exit(0);
}
if( !(theta_new = (double*)malloc(sizeof(double) * (feature_size + 1))) )
{
printf("theta_new* malloc error");
exit(0);
}
int i, j, k, conv;
double diff, sum, alpha = 0.0000001;
for( i = 0; i <= feature_size; i++ )
theta[i] = theta_new[i] = 0.0;
while(1)
{
for( i = 0; i <= feature_size; i++ )
{
sum = 0.0;
for( j = 0; j < data_size; j++ )
{
diff = 0.0;
for( k = 0; k <= feature_size; k++ )
{
diff += feature[j][k] * theta[k];
}
diff = feature[j][feature_size + 1] - diff;
diff *= feature[j][i];
sum += diff;
}
theta_new[i] = theta[i] + alpha * sum;
}
for( i = 0; i <= feature_size; i++ )
printf("%lf ", theta_new[i]);
printf("\n");
for( conv = 1, i = 0; i <= feature_size; i++ )
{
if( fabs(theta_new[i] - theta[i]) > 0.0002 )
{
conv = 0;
break;
}
}
if( 1 == conv )
{
break;
}else
{
for( i = 0; i <= feature_size; i++ )
{
theta[i] = theta_new[i];
}
}
}
for( i = 0; i <= feature_size; i++ )
printf("%lf ", theta[i]);
printf("\n");
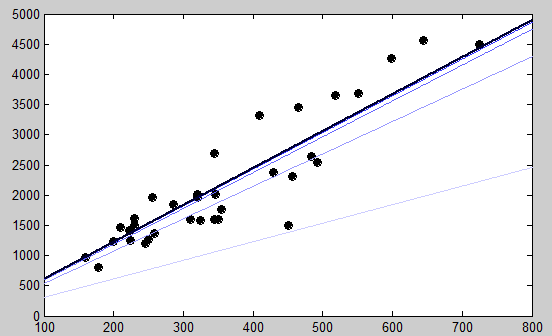
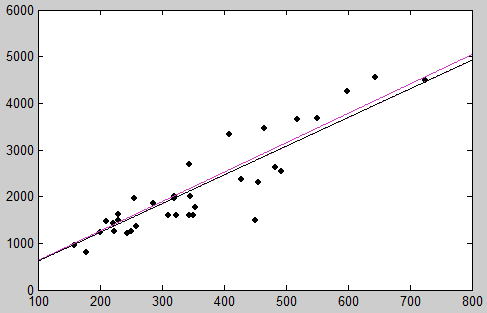
}(擬合情況如上圖,顏色最身的為最後的結果,可以看到一開始的時候幾乎沒有什麼擬合的功能)上面介紹的是批梯度下降演算法,下面介紹另外一種
隨機梯度下降演算法
也叫做增量梯度下降演算法,演算法描述如下:
在該演算法中我們遍歷樣本集合中的每一個樣本,每次使用僅僅一個樣本去更新所有的θ值。然而批梯度下降演算法在更新一個θ時不得不掃描整個訓練集。通常隨機梯度下降演算法比批梯度下降演算法要更快的收斂於接近θ的結果,儘管有可能永遠不會收斂而是在最優值附近擺動。而實際上這已經夠用了,所以當訓練集很大的時候,隨機梯度下降演算法往往是更好的選擇。
以下是C語言實現的隨機梯度下降演算法
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<string.h>
int feature_size;
int data_size;
char filename[20];
double** feature;
double* theta;
double* theta_new;
void readData();
void StochasticGradientDescent();
int main(int argc, char** argv)
{
if( argc != 4 )
{
printf("1.feature_size:\n"
"2.data_size\n"
"3.filename\n");
exit(0);
}
feature_size = atoi(argv[1]);
data_size = atoi(argv[2]);
strcat(filename, argv[3]);
printf("%d,%d,%s\n", feature_size, data_size,filename);
readData();
StochasticGradientDescent();
return 0;
}
void readData()
{
FILE* fread;
if( NULL == (fread = fopen(filename,"r")) )
{
printf("open file error");
exit(0);
}
if( !(feature = (double**)malloc(sizeof(double*) * data_size)) )
{
printf("feature** malloc error");
exit(0);
}
int i;
for( i = 0; i < data_size; i++ )
{
if( !(feature[i] = (double*)malloc(sizeof(double) * (feature_size + 2))) )
{
printf("feature[%d]* malloc error", i);
exit(0);
}
}
int j;
for( i = 0; i < data_size; i++ )
{
feature[i][0] = 1.0;
for( j = 1; j <= feature_size + 1; j++ )
{
if( 1 != fscanf(fread, " %lf ", &feature[i][j]) )
{
printf("fscanf error %d %d", i, j);
exit(0);
}
}
}
for( i = 0; i < data_size; i++ )
{
for( j = 0; j <= feature_size + 1; j++ )
{
printf("%lf\t", feature[i][j]);
}
printf("\n");
}
}
void StochasticGradientDescent()
{
int i, j, k, conv;
if( !(theta = (double*)malloc(sizeof(double) * (feature_size + 1))) )
{
printf("theta* malloc error");
exit(0);
}
if( !(theta_new = (double*)malloc(sizeof(double) * (feature_size + 1))) )
{
printf("theta_new* malloc error");
exit(0);
}
for( i = 0; i <= feature_size; i++ )
theta[i] = theta_new[i] = 0.0;
double diff, alpha = 0.00001;
while(1)
{
for( i = 0; i < data_size; i++ )
{
diff = 0.0;
for( k = 0; k <= feature_size; k++ )
{
diff += theta[k] * feature[i][k];
}
diff -= feature[i][feature_size + 1];
for( j = 0; j <= feature_size; j++ )
{
diff *= feature[i][j];
theta_new[j] = theta[j] - alpha * diff;
}
}
for( i = 0; i <= feature_size; i++ )
printf("%lf ", theta_new[i]);
printf("\n");
for( conv = 1, i = 0; i <= feature_size; i++ )
{
if( fabs(theta_new[i] - theta[i]) > 0.0002 )
{
conv = 0;
break;
}
}
if( 1 == conv )
{
break;
}else
{
for( i = 0; i <= feature_size; i++ )
{
theta[i] = theta_new[i];
}
}
}
}
區域性加權迴歸(LWR)
簡單介紹下引數學習演算法和非引數學習演算法,引數學習演算法是指引數個數固定的一類演算法,非引數學習演算法是指引數數量不固定的一類演算法,區域性加權迴歸演算法是一種特定的非引數學習演算法。
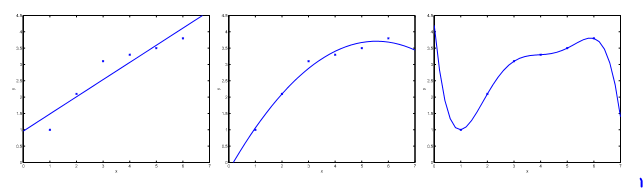
現在考慮根據x對y進行預測的問題,以下的三幅圖中,
最左邊的圖對於資料給出的擬合結果是:
可以看到這些點確實不落在這條直線上,所以我們說擬合的不是很好。之後我們新增一個額外的特徵x2,獲得了一個稍微好點的擬合結果:
然而並不是這樣加的特徵越多就會擬合的越好。最右邊的圖中曲線擬合了一個5次多項式,儘管該擬合曲線經過了每一個點,但是這並不是一個好的擬合結果。最左邊和最右邊分別稱為欠擬合和過擬合。
下面開始介紹LWR。
當面對迴歸問題時,如果是LR演算法,我們需要找到θ使得下面的cost function最小,然後返回θTx就是我們給出的預測值。
但是對於LWR不是這樣的。在LWR中,為了對查詢點做出預測,我們只是考慮了查詢點附近固定長度區域內的資料點(也就是隻考慮了一部分的訓練集合)。之後使用該區域內的點進行線性迴歸來擬合出一條直線。然後根據這條直線上相應的對查詢點的預測值作為演算法的返回值。
正式的定義如下:我們要找到使得如下式子最小的θ:
其中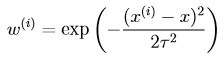
通過觀察可以得到,如果x(i)和查詢點x非常的接近,那麼wi就會非常的大(接近1),反之則會非常的小(接近於0).也就是說線上性迴歸時給距離要預測點遠的資料點較小的權值,離的近的較大的權值。所以該方法通過加權實現了對鄰近點的精確擬合,同時忽略了那些離得很遠的點的貢獻。
之前的線性迴歸演算法是引數學習演算法,因為該演算法有固定的,有限個數的引數,一旦我們得到了引數,當進行以後的預測時就不再需要訓練集合了。但是當時候LWR演算法進行預測的時候,我們需要整個訓練集合。