本章目錄：
1.靜態查詢表
2.動態查詢表
3.雜湊表

基本概念：
查詢表：是由同一型別的資料元素構成的集合
靜態查詢表：只進行“查詢”操作的表
動態查詢表：在查詢過程中，對不存在的資料元素進行插入，或從表中刪除已存在的資料元素，此類操作的表稱為動態查詢表

關鍵字：是資料元素某個資料項的值，可以標識一個數據元素，
主關鍵字：可以唯一標識一個記錄的關鍵字
次關鍵字：可以識別若干記錄的關鍵字

查詢：根據給定的某個值，在表中確定一個其關鍵字等於給定值的記錄或資料元素。

靜態查詢表

順序查詢表：用順序表或連結串列標識靜態查詢表的查詢過程，從表中最後一個記錄開始，逐個進行記錄的關鍵字和給定值的比較，若找到相等的則查詢成功，否則查詢失敗。

定義：為確定記錄在查詢表中的位置，需要和給定值進行比較的關鍵字個數的期望值稱為查詢演算法在查詢成功是的平均查詢長度。Pi是找到第i個記錄的概率，Ci是找到與給定值相等的關鍵字時需要與跟定值比較的關鍵字的個數。

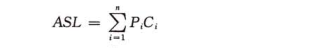
在等概率的情況下順序查詢的平均查詢長度為：

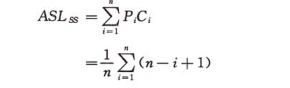
有序表的查詢：
1.折半查詢：先確定待查記錄的所在的範圍，然後逐步縮小範圍直到找到或找不到該記錄為止


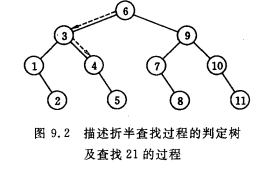
當每個記錄的查詢概率相等時，折半查詢的平均查詢長度：

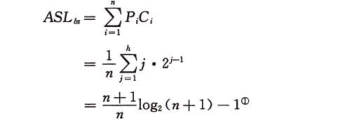
h：是查詢判斷樹的深度

斐波那契查詢：按照斐波那契數列來確定分割點，假設表中記錄個數比某個斐波那契數小於1，即n=Fu-1，則查詢分割點為斐波那契數F(u-1)的值，如此將表中記錄分為了n1和n2兩部分，其中n1中元素數目等於斐波那契數F(u-1) - 1 的值，而n2中元素的個數為斐波那契數F(u-2) - 1的值。如果給定值等於n則查詢成功，如果給定值大於n則在n2中進行斐波那契查詢，如果跟定值小於n則在n1中進行斐波那契查詢。

斐波那契查詢的平均效能高於折半查詢。

靜態樹表的查詢：當有序表中個記錄的查詢概率不相等時，普通折半查詢的效能很可能不是很高。需要建立靜態最優查詢樹。
查詢效能最佳的判定樹是其帶權內路徑長度之和PH值取最小的二叉樹

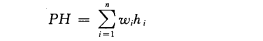
n：是二叉樹上結點的個數
hi：是第i個結點在二叉樹上的層次數
wi=c * pi，pi是結點的查詢概率，c是某個常數。

由於構造靜態最優查詢樹花費的時間代價較高，所以只討論一種PH值近似為最小的次優查詢樹的構造法

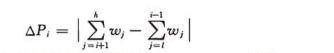
取∆Pi最小的結點 ri 作為根節點進行劃分，然後分別對左右子序列{rlow，rlow+1，…，ri-1}和{ri+1，…，rh}分別構造次優查詢樹。以此不斷遞迴，直到葉子結點。

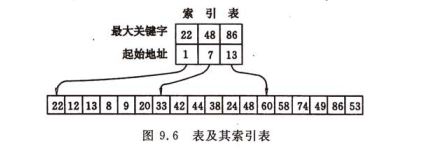
索引順序表的查詢：索引和子表之間有序，子表之內無序，查詢過程分兩步進行
1.確定待查記錄所在的子表
2.在子表中進行順序查詢

動態查詢表
在動態查詢表的查詢過程中，若找到則查詢成功，否則插入關鍵字等於給定值的記錄

二叉排序樹的性質：
1.若左子樹不空，則左子樹上的所有結點均小於根結點
2.若右子樹不空，則右子樹上的所有結點均大於根結點
3.左右子樹分別為二叉排序樹

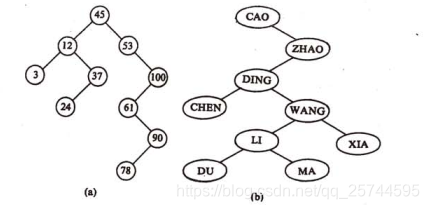
二叉排序樹是一種動態樹表，其結構通常是在查詢過程中生成的。


二叉排序樹刪除結點時，需要將被刪除的結點的左右子樹按一定規則連在被刪結點的雙親結點上。

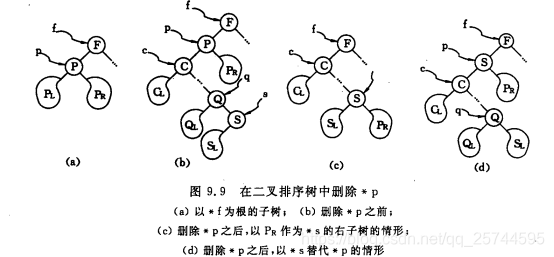
當對有序資料進行構造二叉樹時，會生成單支樹，這時的查詢效能和順序查詢一樣。所以在構造二叉排序樹的過程中需要進行“平衡化”

平衡二叉樹：左右子樹都是平衡二叉樹，且左右子樹的深度只差的絕對值不超過1。
二叉樹的平衡因子BF：值為-1，0， 1，當左子樹比右子樹深度大1層時值為1，相等為0，小一層為-1。當大於1或小於-1時，則為失去平衡，需要調整

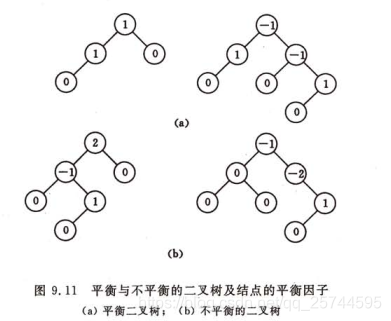
失去平衡進行調整的4種情況：

B-樹的特性（m階）：
1.樹中每個結點至多有m棵子樹
2.若根節點不是葉子結點，則至少有兩棵子樹
3.除根之外的所有非終端結點至少有 (m/2)（向上取整）棵子樹。
4.所有非終端結點中包含下列資訊資料

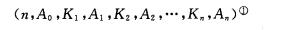
其中n是該結點的關鍵字數，An是指向子樹的指標，Kn是關鍵字。kn關鍵字小於An子樹中的關鍵字，An-1中的關鍵字都小於Kn。

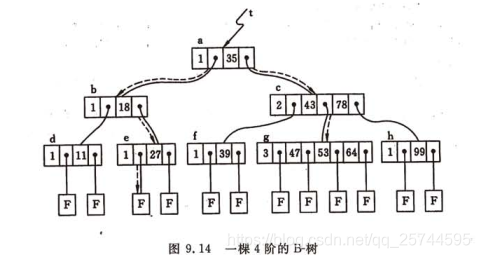
B-樹的查詢包含兩個基本操作：
1.在B-樹中找結點，該動作在磁碟上進行
2.在結點中找關鍵字，該動作在記憶體上進行

B-樹的插入和刪除：
1.插入過程：對於m階樹，先確定插入位置，然後插入該結點，如果結點的關鍵字數目小於m，則插入該結點，若關鍵字數目不小於m，則將中部的一個關鍵字提至雙親，然後剩餘關鍵字分裂為兩個子樹，連線在雙親中，如下圖

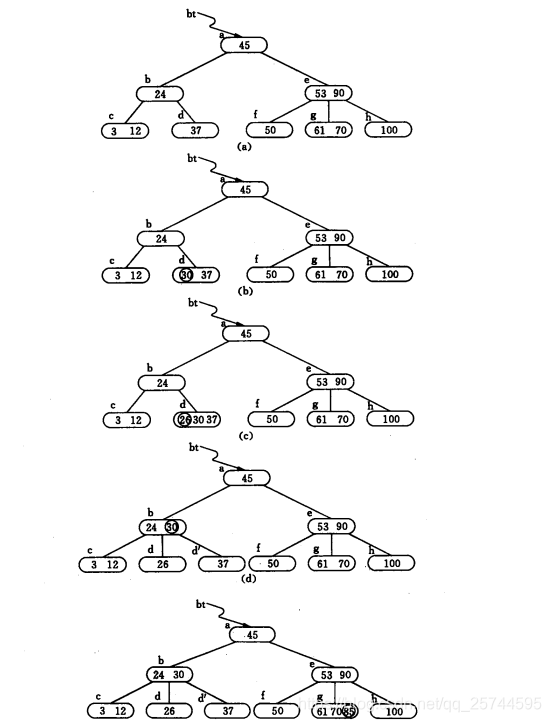
2.刪除結點過程：
a. 若刪除關鍵字所在的結點關鍵字數目不小於[m/2]則只需刪除該關鍵字ki和相應指標Ai。
b. 若結點關鍵字數目等於[m/2] - 1時，而相鄰的右兄弟（左兄弟）結點中關鍵字數目大於[m/2] - 1時，則需將其兄弟結點中最小（最大）的關鍵字上移到雙親結點中，且將雙親中小於（或大於）並緊靠該上移關鍵字的關鍵字下移到被刪關鍵字的結點中。
c. 如果被刪關鍵字所在結點，的兄弟結點關鍵字數目都等於[m/2]-1，假設該結點有右兄弟，且其右兄弟結點地址由雙親結點中的Ai所指，則刪去關鍵字後，它所在的結點中剩餘的關鍵字和指標，加上雙親結點中的關鍵字Ki一起，合併到Ai所指兄弟節點中。如果因此使得雙親結點的關鍵字數目小於[m/2]-1，則以此類推做相應處理。
如下圖

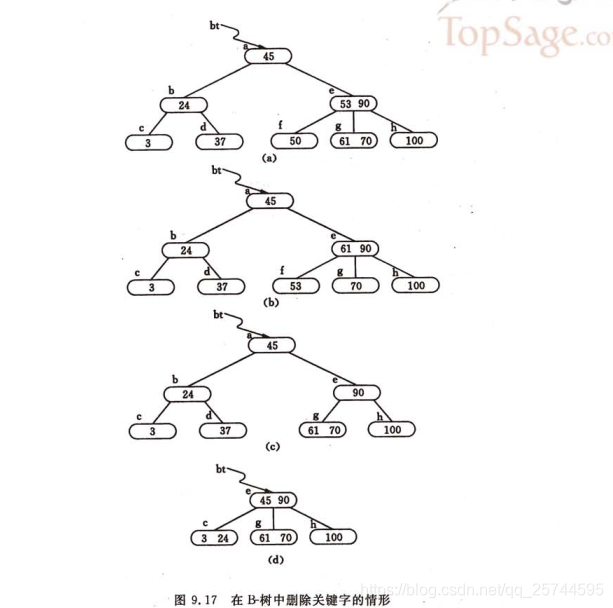
B+樹：是B-樹的變型樹，差異在於：
1.有n棵子樹的結點中包含有n個關鍵字
2.所有的葉子結點中包含了全部關鍵字的資訊，及指向含這些關鍵字記錄的指標，且葉子結點本身依關鍵字的大小自小到大的順序連結。
3.所有非終端結點可以看成是索引部分，結點中僅含有其子樹中的最大或最小關鍵字

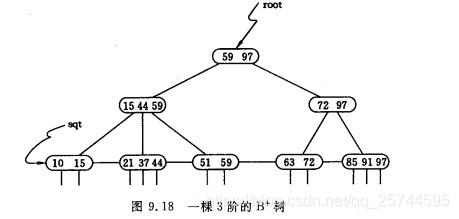
B+樹的查詢、插入和刪除的過程和B-樹類似

鍵樹：又稱為數字查詢樹，樹中的每個結點只含組成關鍵字的一個字元。

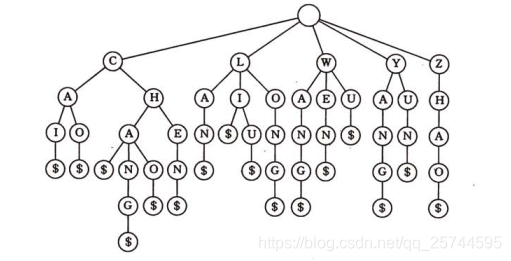
鍵樹的孩子兄弟表示法：

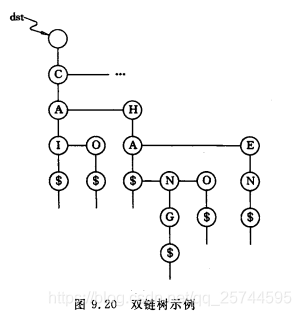
多重連結串列表示鍵樹：

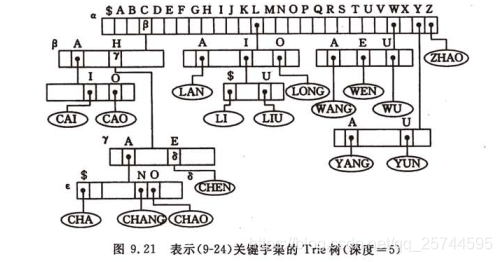
雜湊表
在記錄的儲存位置和它的關鍵字之間建立一個對應關係f，使得每個關鍵字和結構中一個唯一的儲存位置相對應。f稱為雜湊函式。

一個雜湊函式對關鍵字集合中的任一個關鍵字，經過雜湊函式映像到地址集合中的任何一個地址的概率是相等的，則層此類雜湊函式為均勻的雜湊函式。
雜湊函式的構造方法：
1.直接定址法：取關鍵字或關鍵字的某個線性函式值為雜湊地址，例如從1歲到100歲人口數字統計表中，取年齡為關鍵字，雜湊函式取關鍵字自身。

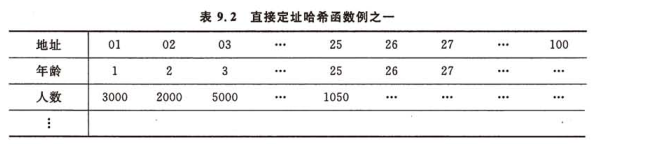
2.數字分析法：如果在雜湊表中可能出現的關鍵字事先知道，則可取其中適合的一部分進行雜湊。
3.平方取中法：取關鍵字平方後的中間幾位為雜湊地址。
4.摺疊法：將關鍵字分割成相同的幾部分，然後取這幾部分的疊加和（捨去進位）作為雜湊地址。
5.除留餘數法：取關鍵字被某個不大於雜湊表長m的數p除後所得的餘數作為雜湊地址

採用雜湊函式通常考慮的因素：
1.計算雜湊函式所需時間
2.關鍵字的長度
3.雜湊表的大小
4.關鍵字的分佈情況
5.記錄的查詢頻率

雜湊函式在雜湊過程中可能出現衝突，即不同關鍵字雜湊後的值相同
處理衝突的方法：
1.開放定址法：例如在除留餘數法中，如果不同關鍵字的餘數相同，則將關鍵字加上i後繼續雜湊，每衝突一次i加1時就是線性探測再雜湊方法。

2.再雜湊法：當衝突產生時，則採用另一個雜湊函式進行雜湊，直到衝突不再發生。
3.鏈地址法：將產生衝突的同義詞，記錄儲存在同一線性連結串列中

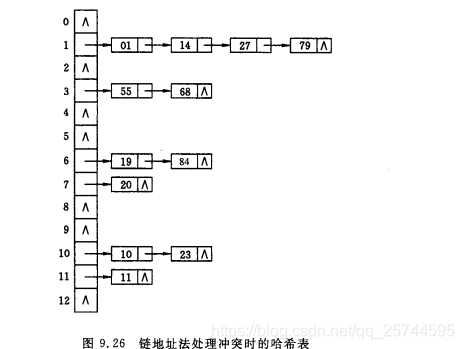
4.建立一個公共溢位區：在雜湊過程中，若產生衝突，則將其填入溢位表。

雜湊表的查詢及分析：將給定的K值，根據造表時的雜湊函式求得雜湊地址，若此位置上沒有記錄，則查詢不成功，否則比較關鍵字，若相等則查詢成功，若不相等，則根據處理衝突的方法找到下一個地址，知道雜湊地址為“空”或等於給定值。