在查詢NavMesh資料的時候看到這篇blog寫的不錯，從原理到實現，很詳細。另外也可以參考：基於導航網格的A星尋路，這篇blog的參考文獻有詳細介紹導航網格。以下內容轉自http://blianchen.blog.163.com/ by 竹石

NAV導航網格尋路（1） -- 介紹

WayPoint尋路

下圖是一個典型的路點尋路

另一種方法是使用多邊形來記錄路徑資訊，它可以提供更多的資訊給ai角色使用。下圖就是一個navigation mesh。

以下列出幾個WayPoint的不足之處：

1. 一些複雜的遊戲地圖需要的WayPoint數量過於龐大
2. 有時會使角色走“Z”型路徑

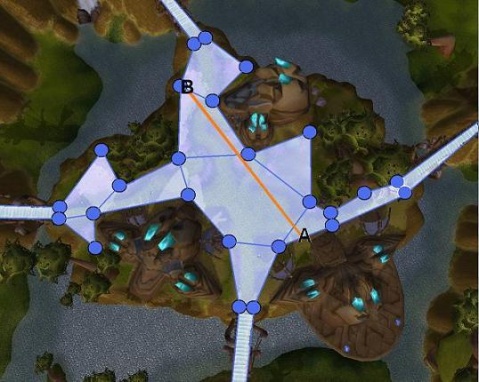
如下圖A點和B點之間的路徑

NAV尋路如下圖

下圖是路點尋路，如黃線，會產生“Z”字形

下圖為文章開始時展示的地圖的比較，紅線是wayPoint尋路，藍線是nav。

3. 不能進行動態修正，如果地圖中有動態障礙，處理起來會很困難

    如要實現即時戰略遊戲中，一輛在路上行走的坦克會擋住你軍隊的去路，這個移動的坦克就是一個動態障礙。

4. 不能根據角色的特性（不同寬度、高度等）改變路徑

如一個狹窄的通道，普通的人能夠通過，而一輛馬車的寬度超過通道寬度，應該不能通過。

5. 不能儲存地形的附加資訊，如地表高度、地面特徵（水面、沙地等）

    比如一個遊戲中的角色在走到沙地上時會降低移動速度，或走在一個斜坡上時人物會發生傾斜等。

NAV導航網格尋路（2） -- 尋路方法

nav尋路一般包含兩部分，首先是使用工具根據地圖資訊生成尋路用的nav mesh，接下來就是在遊戲中根據生成的nav mesh來自動尋路。

一般人首先關心的就是尋路方法，所以這裡把順序顛倒下，先說尋路。

一.  使用A*尋找所經過網格路徑

 下圖為一個已經生成nav網格的地圖，深紅色區域為不可行走區域，淺紅色區域為可以行走的區域。

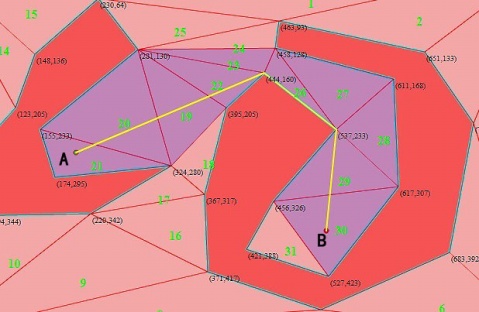
如下圖，現在如果要尋找從A點到B點的路徑，首先要從所有可行走的網格中找到一條最優的網格路徑（圖中紫色的網格），然後再根據這些網格生成所需要的路徑點。

計算最優網格路徑的方法可以使用流行的A*，也可以使用其它方法。A*演算法網上很多就不說了，至於三角網格的A*實現因為涉及網格的資料結構會在系列的最後給出。

二.  生成路徑點

nav尋路最常用的就是光照射線法了，這個在neoragex2002的blog上有講，這裡就不說了

另一種方法就是拐角點法，如下圖

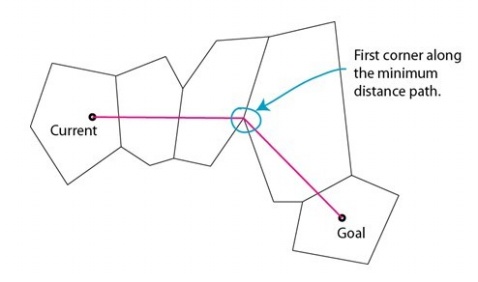
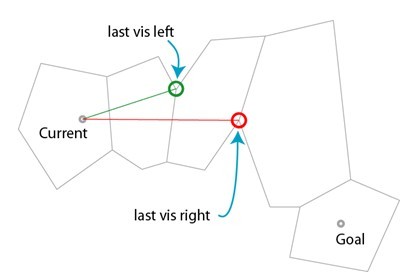
下圖的5個凸多邊形是已經生成的導航網格，多邊形外部的區域為不可行走區域，current為起點，goal為終點，從圖中就可以看出最短路徑為圖中紅線，藍色圈出的點為我們需要找出的點。所有多邊形頂點均按逆時針方向儲存（這些均在生成導航網格時處理，以後會講到）。

（1）下圖顯示出各區域之間的入口，即多邊形的臨邊。由圖中可以看出每個臨邊均為起點穿出該多邊形區域的邊，故以下稱該邊為穿出邊。

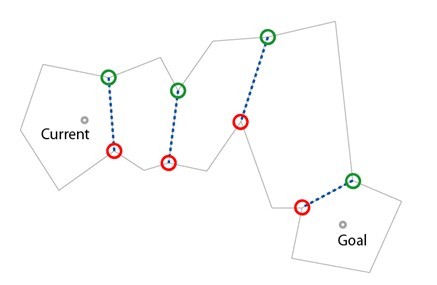
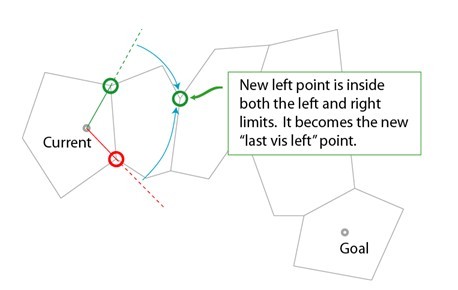
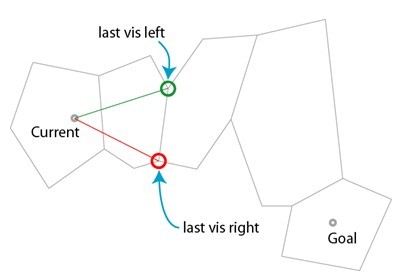
（2）首先找到起始點所在的多邊形和穿出邊的兩個端點，由起點連線兩個端點，形成兩個線段lineLeft 和lineRight。如下圖。綠色圈表示左點，紅色表示右點（左點、右點是根據多邊形頂點儲存順序而來）。

（3）繼續找到下一個穿出邊的兩個端點，判斷新的左點是否在lineLeft 和lineRigh之間，如果在，則更新lineLeft為起點到新左點的線段。

同樣處理新穿出邊的右點，如下圖

該步最後得到兩個新的線段，如下圖。

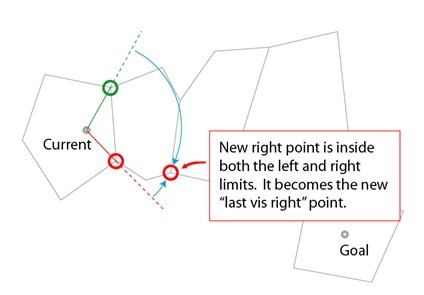
（4） 繼續判斷下一個穿出邊的兩個端點，如下圖，新的左點在lineLeft和lineRight的外面，則不更新線段。

下圖說明新的右點在兩條直線之間，更新lineRight。

該步最後得到兩個新的線段，如下圖。

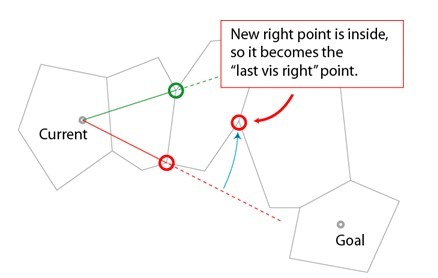
（5） 繼續迴圈判斷下一個穿出邊的兩個端點，該穿出邊的兩個端點都在lineRight的右側，表示lineRight的終點即為路徑的一個拐角點。

（6） 迴圈以上步驟都可以找到從起點到終點的一條完整路徑。

NAV導航網格尋路（3） -- 一些必要的計算幾何知識

在繼續下面的nav網格生成演算法之前，先介紹一下涉及到的計算幾何知識。這裡只羅列出結論，要詳細瞭解參考相關書籍。

• 向量加減法：
  　設二維向量P = ( x1, y1 )，Q = ( x2 , y2 )，則向量加法定義為： P + Q = ( x1 + x2 , y1 + y2 )，同樣的，向量減法定義為： P - Q = ( x1 - x2 , y1 - y2 )。顯然有性質 P + Q = Q + P，P - Q = - ( Q - P )。
• 向量叉積
  設向量P = ( x1, y1 )，Q = ( x2, y2 )，則向量叉積定義為由(0,0)、p1、p2和p1+p2所組成的平行四邊形的帶符號的面積，即：P × Q = x1*y2 - x2*y1，其結果是一個標量。顯然有性質 P × Q = - ( Q × P ) 和 P × ( - Q ) = - ( P × Q )。
• 折線段的拐向判斷：
  　　折線段的拐向判斷方法可以直接由向量叉積的性質推出。對於有公共端點的線段p0p1和p1p2，通過計算(p2 - p0) × (p1 - p0)的符號便可以確定折線段的拐向：
  　　若(p2 - p0) × (p1 - p0) > 0,則p0p1在p1點拐向右側後得到p1p2。
  　　若(p2 - p0) × (p1 - p0) < 0,則p0p1在p1點拐向左側後得到p1p2。
  　　若(p2 - p0) × (p1 - p0) = 0,則p0、p1、p2三點共線。
• 判斷兩線段是否相交：
  　　我們分兩步確定兩條線段是否相交：
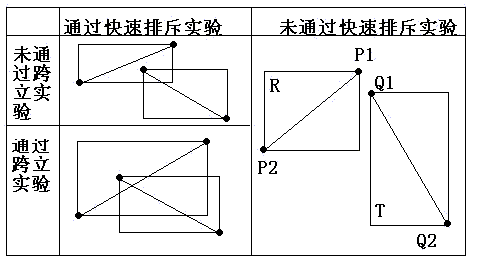
  　　(1)快速排斥試驗
  　　　　設以線段 P1P2 為對角線的矩形為R， 設以線段 Q1Q2 為對角線的矩形為T，如果R和T不相交，顯然兩線段不會相交。
  　　(2)跨立試驗
  　　　　如果兩線段相交，則兩線段必然相互跨立對方。若P1P2跨立Q1Q2 ，則向量 ( P1 - Q1 ) 和( P2 - Q1 )位於向量( Q2 - Q1 ) 的兩側，即( P1 - Q1 ) × ( Q2 - Q1 ) * ( P2 - Q1 ) × ( Q2 - Q1 ) < 0。上式可改寫成( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) > 0。當 ( P1 - Q1 ) × ( Q2 - Q1 ) = 0 時，說明 ( P1 - Q1 ) 和 ( Q2 - Q1 )共線，但是因為已經通過快速排斥試驗，所以 P1 一定線上段 Q1Q2上；同理，( Q2 - Q1 ) ×(P2 - Q1 ) = 0 說明 P2 一定線上段 Q1Q2上。所以判斷P1P2跨立Q1Q2的依據是：( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) >= 0。同理判斷Q1Q2跨立P1P2的依據是：( Q1 - P1 ) × ( P2 - P1 ) * ( P2 - P1 ) × ( Q2 - P1 ) >= 0。
  
  
• 凸多邊形
  假設我們在一個多邊形上(包括多邊形的邊界及邊界圍封的範圍)任意取兩點並以一條線段連結該兩點，如果線段上的每一點均在該多邊形上，那麼我們便說這個多邊形是凸的。
• 凸包
  給定平面上的一個(有限)點集(即一組點)，這個點集的凸包就是包含點集中所有點的最小面積的凸多邊形。
  
  
• 點在凸多邊形中的判斷
  假設多邊形是凸的，而且頂點p0,p1,...,pn按順時針方向排列，則點在多邊形任意一邊 pi-1, pi 的右面。
• Voronoi圖及對偶圖
  
  
• Delaunay三角剖分（Voronoi對偶圖）
  
  在實際中運用的最多的三角剖分是Delaunay三角剖分，它是一種特殊的三角剖分。先從Delaunay邊說起：
      【定義】Delaunay邊：假設E中的一條邊e（兩個端點為a,b），e若滿足下列條件，則稱之為Delaunay邊：存在一個圓經過a,b兩點，圓內(注意是圓內，圓上最多三點共圓)不含點集V中任何其他的點，這一特性又稱空圓特性。
      【定義】Delaunay三角剖分：如果點集V的一個三角剖分T只包含Delaunay邊，那麼該三角剖分稱為Delaunay三角剖分。
  以下是Delaunay剖分所具備的優異特性：
      1.最接近：以最近臨的三點形成三角形，且各線段(三角形的邊)皆不相交。
      2.唯一性：不論從區域何處開始構建，最終都將得到一致的結果。
      3.最優性：任意兩個相鄰三角形形成的凸四邊形的對角線如果可以互換的話，那麼兩個三角形六個內角中最小的角度不會變大。
      4.最規則：如果將三角網中的每個三角形的最小角進行升序排列，則Delaunay三角網的排列得到的數值最大。
      5.區域性：新增、刪除、移動某一個頂點時只會影響臨近的三角形。
      6.具有凸多邊形的外殼：三角網最外層的邊界形成一個凸多邊形的外殼。
• 多邊形裁剪
  
  Weiler-Athenton演算法

–主多邊形：被裁剪多邊形，記為A

–裁剪多邊形：裁剪視窗，記為B

多邊形頂點的排列順序（使多邊形區域位於有向邊的左側 ）外環：逆時針 ；內環：順時針

主多邊形和裁剪多邊形把二維平面分成兩部分。

內裁剪：A∩B

外裁剪：A-B

裁剪結果區域的邊界由A的部分邊界和B的部分邊界兩部分構成，並且在交點處邊界發生交替，即由A的邊界轉至B的邊界，或由B的邊界轉至A的邊界。

如果主多邊形與裁剪多邊形有交點，則交點成對出現，它們被分為如下兩類：

進點：主多邊形邊界由此進入裁剪多邊形內  如，I1,I3, I5, I7, I9, I11

出點：主多邊形邊界由此離開裁剪多邊形區域. 如， I0,I2, I4, I6, I8, I10 

演算法步驟

(1)建立空的裁剪結果多邊形的頂點表．

(2)選取任一沒有被跟蹤過的交點為始點，將其輸出到結果多邊形頂點表中．

(3)如果該交點為進點，跟蹤主多邊形邊邊界；否則跟蹤裁剪多邊形邊界．

(4) 跟蹤多邊形邊界，每遇到多邊形頂點，將其輸出到結果多邊形頂點表中，直至遇到新的交點．

(5)將該交點輸出到結果多邊形頂點表中，並通過連線該交點的雙向指標改變跟蹤方向（如果上一步跟蹤的是主多邊形邊界，現在改為跟蹤裁剪多邊形邊界；如果上一步跟蹤裁剪多邊形邊界，現在改為跟蹤主多邊形邊界）．

(6)重複(4)、(5)直至回到起點

NAV導航網格尋路（4） -- 生成nav網格

假設上圖是一個遊戲地圖，紅色的區域是不可行走的區域，淺灰色區域是可行走區域，要想在遊戲中實現nav尋路，必須將可行走區域轉化為nav網格並儲存為一種固定形式的資料，如下圖淺紅色的三角形。

nav網格必須是凸多邊形，這裡使用三角型，當然也可以使用4邊形。下面介紹一種任意多邊形的三角化演算法。演算法來自論文《平面多邊形域的快速約束Delaunay三角化》作者：曾薇 孟祥旭 楊承磊 楊義軍。詳細內容請參考該論文。

先來看幾個定義：

A. 我們稱點 p3 為直線 p1p2 的可見點，其必須滿足下面三個條件：

（1） p3 在邊 p1p2 的右側 (頂點順序為順時針)；

（2） p3 與 p1 可見，即 p1p3 不與任何一個約束邊相交；

（3） p3 與 p2 可見

B. DT點

在一個約束Delaunay三角形中，其中與一條邊相對的頂點稱為該邊的DT點。

確定 DT 點的過程如下：

Step1.  構造 Δp1p2p3 的外接圓 C（p1，p2，p3）及其網格包圍盒 B（C（p1，p2，p3））

Step2. 依次訪問網格包圍盒內的每個網格單元：

            對未作當前趟數標記的網格單元進行搜尋，並將其標記為當前趟數

           若某個網格單元中存在可見點 p, 並且 ∠p1pp2 > ∠p1p3p2，則令 p3=p1，轉Step1；否則，轉Step3.

Step3.  若當前網格包圍盒內所有網格單元都已被標記為當前趟數，也即C（p1，p2，p3）內無可見點，則 p3 為的 p1p2 的 DT 點

生成Delaunay三角網格演算法如下：

Step2. 取任意一條外邊界邊 p1p2 .

Step3.  計算 DT 點 p3，構成約束 Delaunay 三角形 Δp1p2p3 .

Step4. 如果新生成的邊 p1p3 不是約束邊，若已經在堆疊中，則將其從中刪除；否則，將其放入堆疊；類似地，可處理 p3p2 .

Step5. 若堆疊不空，則從中取出一條邊，轉Step3；否則，演算法停止 .

程式實現該演算法（AS3語言）

1。資料結構

不難看出，要想實現該演算法首先要確定一些基礎物件，如點、線、三角型和多邊形等物件。（才發現這個blog中竟然沒有程式碼的格式）

二維點的定義 public class Vector2f {}  包括向量加減、叉積等方法。

線的定義  public class Line2D {} 包括下面方法：

    classifyPoint(point:Vector2f, epsilon:Number = 0.000001):int
                 判斷點與直線的關係，假設你站在a點朝向b點， 則輸入點與直線的關係分為：Left, Right or Centered on the line
           equals(line:Line2D):Boolean
                 線段是否相等 （忽略方向）
           getDirection():Vector2f
                  直線方向
           intersection(other:Line2D, pIntersectPoint:Vector2f = null):int
                  判斷兩個直線關係 this line A = x0, y0 and B = x1, y1 other is A = x2, y2 and B = x3, y3
           length():Number
                  直線長度
           signedDistance(point:Vector2f):Number
                  給定點到直線的帶符號距離，從a點朝向b點，右向為正，左向為負 

三角型定義 public class Triangle：

    getSide(sideIndex:int):Line2D
                  取得指定索引的邊(從0開始，順時針)
            getVertex(i:int):Vector2f
                   根據i返回頂點
            isPointIn(testPoint:Vector2f):Boolean
                   測試給定點是否在三角型中
            setVertex(i:int, point:Vector2f):void
                   根據i指定的索引設定三角形的頂點  

多邊形定義  public class Polygon：

     public vertexV : Vector.<Vector2f>   //頂點列表，按順時針方向排序

     cw():void 
                 將多邊形的頂點按逆時針排序
            isCW():Boolean
                 將多邊形的頂點按順時針排序
            isSimplicity():Boolean
                 是否是簡單多邊形
            rectangle():Rectangle
                  返回矩形包圍盒  Polygon 
            union(polygon:Polygon):Vector.<Polygon>
                  合併兩個多邊形(Weiler-Athenton演算法) 

三角化的完整程式碼，註釋比較全，就不再詳細解釋了 

<span style="background-color: rgb(255, 255, 255);">/*
* @author 白連忱 
* date Jan 22, 2010
*/
package org.blch.geom
{
    import flash.display.Sprite;
    import flash.geom.Rectangle;
    import flash.text.TextField;
    import flash.text.TextFieldAutoSize;
    import flash.text.TextFormat;
    
    /**
     * Delaunay
     * @langversion ActionScript 3.0
     * @playerversion Flash 10.0
     */
    public class Delaunay
    {
        public function Delaunay()
        {
        }
        
        private static const EPSILON:Number = 0.000001;    //精度
        
        private var polygonV:Vector.<Polygon>;        //所有多邊形，第0個元素為區域外邊界 (輸入資料)
        
        private var vertexV:Vector.<Vector2f>;        //所有頂點列表, 前outEdgeVecNmu個為外邊界頂點
        private var edgeV:Vector.<Line2D>;            //所有約束邊
        
        private var outEdgeVecNmu:int;            //區域外邊界頂點數
        
        private  var lineV:Vector.<Line2D>;    //線段堆疊
        
        private var triangleV:Vector.<Triangle>;     //生成的Delaunay三角形
        
        public function createDelaunay(polyV:Vector.<Polygon>):Vector.<Triangle> {
            //Step1.     建立單元大小為 E*E 的均勻網格，並將多邊形的頂點和邊放入其中.
            //            其中 E=sqrt(w*h/n)，w 和 h 分別為多邊形域包圍盒的寬度、高度，n 為多邊形域的頂點數 .
            initData(polyV);
            
            //Step2.    取任意一條外邊界邊 p1p2 .
            var initEdge:Line2D = getInitOutEdge();
            lineV.push(initEdge);
            
            var edge:Line2D;
            do {
                //Step3.     計算 DT 點 p3，構成約束 Delaunay 三角形 Δp1p2p3 .
                edge = lineV.pop();
//                trace("開始處理edge###########:", edge);
                var p3:Vector2f = findDT(edge);
                if (p3 == null) continue;
                var line13:Line2D = new Line2D(edge.getPointA(), p3);
                var line32:Line2D = new Line2D(p3, edge.getPointB());
                
                //Delaunay三角形放入輸出陣列
                var trg:Triangle = new Triangle(edge.getPointA(), edge.getPointB(), p3);
                
//                trace("DT 點p3", p3);
//                trace("Triangle", trg);
                triangleV.push(trg);
                
                //Step4.    如果新生成的邊 p1p3 不是約束邊，若已經在堆疊中，
                //            則將其從中刪除；否則，將其放入堆疊；類似地，可處理 p3p2 .
                var index:int;
                if (indexOfVector(line13, this.edgeV) < 0) {
                    index = indexOfVector(line13, lineV);
                    if (index > -1) {
                        lineV.splice(index, 1);
                    } else {
                        lineV.push(line13);
                    }
                }
                if (indexOfVector(line32, this.edgeV) < 0) {
                    index = indexOfVector(line32, lineV);
                    if (index > -1) {
                        lineV.splice(index, 1);
                    } else {
                        lineV.push(line32);
                    }
                }
            
            //Step5.    若堆疊不空，則從中取出一條邊，轉Step3；否則，演算法停止 .
//                trace("處理結束edge###########\n");
            } while (lineV.length > 0);
                
            return triangleV;
        }
        
        /**
         * 初始化資料
         * @param polyV
         */        
        private function initData(polyV:Vector.<Polygon>):void {
            //填充頂點和線列表
            vertexV = new Vector.<Vector2f>();
            edgeV = new Vector.<Line2D>();
            var poly:Polygon;
            for (var i:int=0; i<polyV.length; i++) {
                poly = polyV[i];
                putVertex(vertexV, poly.vertexV);
                putEdge(edgeV, poly.vertexV);
            }
            
            outEdgeVecNmu = polyV[0].vertexNmu;
            
            lineV = new Vector.<Line2D>();
            triangleV = new Vector.<Triangle>();
        }
        
        /**
         * 獲取初始外邊界
         * @return 
         */        
        private function getInitOutEdge():Line2D {
            var initEdge:Line2D = edgeV[0];
            //檢查是否有頂點p在該邊上，如果有則換一個外邊界
            var loopSign:Boolean;
            var loopIdx:int = 0;
            do {
                loopSign = false;
                loopIdx++;
                for each (var testV:Vector2f in this.vertexV) {
                    if ( testV.equals(initEdge.getPointA()) || testV.equals(initEdge.getPointB()) ) continue;
                    if (initEdge.classifyPoint(testV, EPSILON) == PointClassification.ON_LINE) {
                        loopSign = true;
                        initEdge = edgeV[loopIdx];
                        break;
                    }
                }
            } while (loopSign && loopIdx<outEdgeVecNmu-1);    //只取外邊界
            return initEdge;
        }
        
        /**
         * 將srcV中的點放入dstV
         * @param dstV
         * @param srcV
         */        
        private function putVertex(dstV:Vector.<Vector2f>, srcV:Vector.<Vector2f>):void {
            for each (var item:Vector2f in srcV) {
                dstV.push(item);
            }
        }
        
        /**
         * 根據srcV中的點生成多邊形線段，並放入dstV
         * @param dstV
         * @param srcV
         */        
        private function putEdge(dstV:Vector.<Line2D>, srcV:Vector.<Vector2f>):void {
            if (srcV.length < 3) return;    //不是一個多邊形
            
            var p1:Vector2f = srcV[0];
            var p2:Vector2f;
            for (var i:int=1; i<srcV.length; i++) {
                p2 = srcV[i];
                dstV.push(new Line2D(p1, p2));
                p1 = p2;
            }
            p2 = srcV[0];
            dstV.push(new Line2D(p1, p2));
        }
        
        /**
         * 判斷線段是否是約束邊
         * @param line
         * @return 線段的索引，如果沒有找到，返回-1
         */        
        private function indexOfVector(line:Line2D, vector:Vector.<Line2D>):int {
            var lt:Line2D;
            for (var i:int=0; i<vector.length; i++) {
                lt = vector[i];
                if (lt.equals(line)) return i;
            }
            return -1;
        }
        
        /**
         * 計算 DT 點
         * @param line
         * @return 
         */        
        private function findDT(line:Line2D):Vector2f {
            var p1:Vector2f = line.getPointA();
            var p2:Vector2f = line.getPointB();
            
            //搜尋所有可見點             TODO 按y方向搜尋距線段終點最近的點
            var allVPoint:Vector.<Vector2f> = new Vector.<Vector2f>();        // line的所有可見點
            for each (var vt:Vector2f in this.vertexV) {
                if (isVisiblePointOfLine(vt, line)) {
                    allVPoint.push(vt);
                }
            }

            if (allVPoint.length == 0) return null;
            
            var p3:Vector2f = allVPoint[0];   

            var loopSign:Boolean = false;
            do {
                loopSign = false;
                
                //Step1. 構造 Δp1p2p3 的外接圓 C（p1，p2，p3）及其網格包圍盒 B（C（p1，p2，p3））
                var circle:Circle = this.circumCircle(p1, p2, p3);
                var boundsBox:Rectangle = this.circleBounds(circle);
                
                //Step2. 依次訪問網格包圍盒內的每個網格單元：
                //         若某個網格單元中存在可見點 p, 並且 ∠p1pp2 > ∠p1p3p2，則令 p3=p，轉Step1；否則，轉Step3.
                var angle132:Number = Math.abs(lineAngle(p1, p3, p2));    // ∠p1p3p2
                for each (var vec:Vector2f in allVPoint) {
                    if ( vec.equals(p1) || vec.equals(p2) || vec.equals(p3) ) {
                        continue;
                    }
                    //不在包圍盒中
                    if (boundsBox.contains(vec.x, vec.y) == false) {
                        continue;
                    }
                    
                    //夾角
                    var a1:Number = Math.abs(lineAngle(p1, vec, p2));
                    if (a1 > angle132) {
                        /////轉Step1
                        p3 = vec;
                        loopSign = true;
                        break;
                    }
                }
                ///////轉Step3
            } while (loopSign); 
            
            //Step3. 若當前網格包圍盒內所有網格單元都已被處理完，
            //         也即C（p1，p2，p3）內無可見點，則 p3 為的 p1p2 的 DT 點
            return p3;
        }
        
        /**
         * 返回頂角在o點，起始邊為os，終止邊為oe的夾角, 即∠soe (單位：弧度) 
         * 角度小於pi，返回正值;   角度大於pi，返回負值 
         */        
        private function lineAngle(s:Vector2f, o:Vector2f, e:Vector2f):Number 
        { 
            var cosfi:Number, fi:Number, norm:Number; 
            var dsx:Number = s.x - o.x; 
            var dsy:Number = s.y - o.y; 
            var dex:Number = e.x - o.x; 
            var dey:Number = e.y - o.y; 
            
            cosfi = dsx*dex + dsy*dey; 
            norm = (dsx*dsx + dsy*dsy) * (dex*dex + dey*dey); 
            cosfi /= Math.sqrt( norm ); 
            
            if (cosfi >=  1.0 ) return 0; 
            if (cosfi <= -1.0 ) return -Math.PI; 
            
            fi = Math.acos(cosfi); 
            if (dsx*dey - dsy*dex > 0) return fi;      // 說明向量os 在向量 oe的順時針方向 
            return -fi; 
        } 
        
        /**
         * 返回圓的包圍盒
         * @param c
         * @return 
         */        
        private function circleBounds(c:Circle):Rectangle {
            return new Rectangle(c.center.x-c.r, c.center.y-c.r, c.r*2, c.r*2);
        }
        
        /**
         * 返回三角形的外接圓
         * @param p1
         * @param p2
         * @param p3
         * @return 
         */        
        private function circumCircle(p1:Vector2f, p2:Vector2f, p3:Vector2f):Circle {
            var m1:Number,m2:Number,mx1:Number,mx2:Number,my1:Number,my2:Number;
            var dx:Number,dy:Number,rsqr:Number,drsqr:Number;
            var xc:Number, yc:Number, r:Number;
            
            /* Check for coincident points */
            
            if ( Math.abs(p1.y-p2.y) < EPSILON && Math.abs(p2.y-p3.y) < EPSILON )
            {
                trace("CircumCircle: Points are coincident.");
                return null;
            }
            
            m1 = - (p2.x - p1.x) / (p2.y - p1.y);
            m2 = - (p3.x-p2.x) / (p3.y-p2.y);
            mx1 = (p1.x + p2.x) / 2.0;
            mx2 = (p2.x + p3.x) / 2.0;
            my1 = (p1.y + p2.y) / 2.0;
            my2 = (p2.y + p3.y) / 2.0;
            
            if ( Math.abs(p2.y-p1.y) < EPSILON ) {
                xc = (p2.x + p1.x) / 2.0;
                yc = m2 * (xc - mx2) + my2;
            } else if ( Math.abs(p3.y - p2.y) < EPSILON ) {
                xc = (p3.x + p2.x) / 2.0;
                yc = m1 * (xc - mx1) + my1;    
            } else {
                xc = (m1 * mx1 - m2 * mx2 + my2 - my1) / (m1 - m2);
                yc = m1 * (xc - mx1) + my1;
            }
            
            dx = p2.x - xc;
            dy = p2.y - yc;
            rsqr = dx*dx + dy*dy;
            r = Math.sqrt(rsqr);
            
            return new Circle(new Vector2f(xc, yc), r);
        }
        
        /**
         * 判斷點vec是否為line的可見點
         * @param vec
         * @param line
         * @return true:vec是line的可見點
         */        
        private function isVisiblePointOfLine(vec:Vector2f, line:Line2D):Boolean {
            if (vec.equals(line.getPointA()) || vec.equals(line.getPointB())) {
                return false;
            }
            
            //（1） p3 在邊 p1p2 的右側 (多邊形頂點順序為順時針)；
            if (line.classifyPoint(vec, EPSILON) != PointClassification.RIGHT_SIDE)
            {
                return false;
            }
            
            //（2） p3 與 p1 可見，即 p1p3 不與任何一個約束邊相交；
            if (isVisibleIn2Point(line.getPointA(), vec) == false) {
                return false;
            }
            
            //（3） p3 與 p2 可見
            if (isVisibleIn2Point(line.getPointB(), vec) == false) {
                return false;
            }
            
            return true;
        }
        
        /**
         * 點pa和pb是否可見(pa和pb構成的線段不與任何約束邊相交，不包括頂點)
         * @param pa
         * @param pb
         * @return 
         */
        private function isVisibleIn2Point(pa:Vector2f, pb:Vector2f):Boolean {
            var linepapb:Line2D = new Line2D(pa, pb);
            var interscetVector:Vector2f = new Vector2f();        //線段交點
            for each (var lineTmp:Line2D in this.edgeV) {
                //兩線段相交
                if (linepapb.intersection(lineTmp, interscetVector) == LineClassification.SEGMENTS_INTERSECT) {
                    //交點是不是端點
                    if ( !pa.equals(interscetVector) && !pb.equals(interscetVector) ) {
                        return false;
                    }
                }
            }
            return true;
        }
        
    }
}

import org.blch.geom.Vector2f;
/**
 * 圓
 * @author blc
 */
class Circle {
    public var center:Vector2f;        //圓心
    public var r:Number;            //半徑
        
    public function Circle(cen:Vector2f, r:Number) {
        this.center = cen;
        this.r = r;
    }
}</span>

NAV導航網格尋路（5） -- 生成網格的一些補充

如果你也實現了上一章提到的程式碼，不難發現對下圖的兩種情況會出現問題

左面的是兩個區域有相交的情況，右面的是多邊形本身有自交，在這兩種情況下，前面給出的程式碼均會產生錯誤的結果。

對於兩個多邊形相交，可以在生成網格之前先合併多邊形，合併後如圖

合併演算法在前面多邊形剪裁處已給出一個，這裡只貼上程式碼：

<span style="background-color: rgb(255, 255, 255);">         /**
         * 合併兩個多邊形(Weiler-Athenton演算法)
         * @param polygon
         * @return 
         *             null--兩個多邊形不相交，合併前後兩個多邊形不變
         *             Polygon--一個新的多邊形
         */        
        public function union(polygon:Polygon):Vector.<Polygon> {
            //包圍盒不相交
            if (rectangle().intersection(polygon.rectangle()) == false) {
                return null;
            }
            
            //所有頂點和交點
            var cv0:Vector.<Node> = new Vector.<Node>();//主多邊形
            var cv1:Vector.<Node> = new Vector.<Node>();//合併多邊形
            //初始化
            var node:Node;
            for (var i:int=0; i<this.vertexV.length; i++) {
                node = new Node(this.vertexV[i], false, true);
                if (i > 0) {
                    cv0[i-1].next = node;
                }
                cv0.push(node);
            }
            for (var j:int=0; j<polygon.vertexV.length; j++) {
                node = new Node(polygon.vertexV[j], false, false);
                if (j > 0) {
                    cv1[j-1].next = node;
                }
                cv1.push(node);
            }
            
            //插入交點
            var insCnt:int = this.intersectPoint(cv0, cv1);