剛開始的時候一直不明白插點的順序為什麼不會對最後的結果有影響----一直不懂這個演算法---

今天看見他們都學會了-.-終於把我也帶會了--

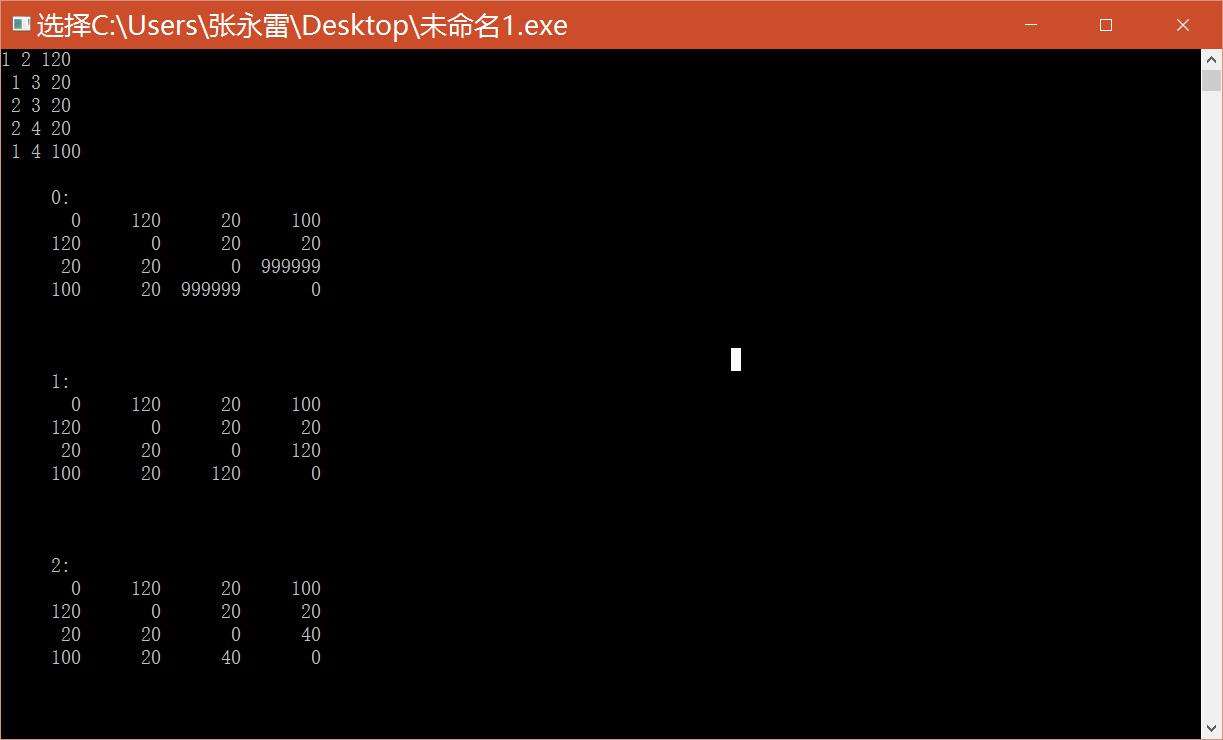
對於原理的理解我還是通過輸出每一步更新後的結果搞明白的

開始一直不懂的是：

對於A-D：

更新B時--AB+BD>AD   不更新

更新C時--AC+CB<AB   AB 更新

但是就不能再--AB+BD < AD 來更新了呀--

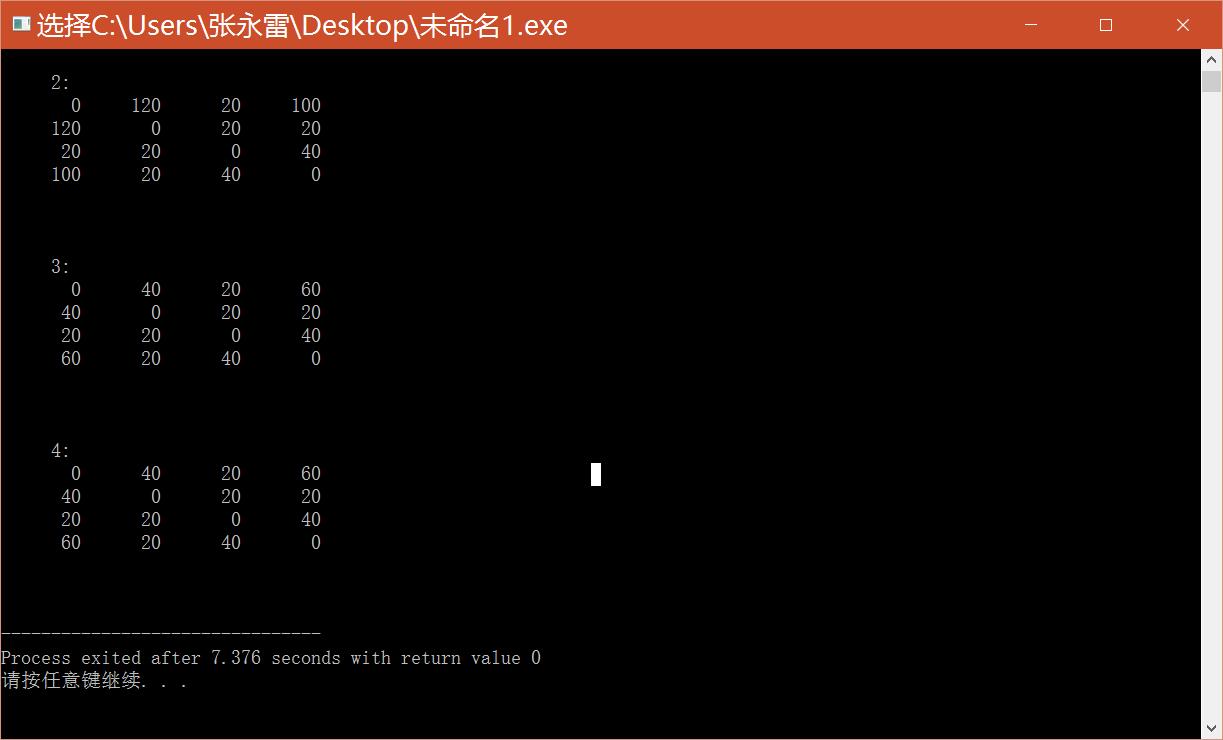
看了詳細的更新過程發現--更新B的時候CB+BD<CD ---CD 就更新了--為40

更新C時就AC+CD<AD ---AD 就更新為60了--

對於任意兩個點A,B，如果有A-----a----b------c-----d------B

這條最短路線---不管a，b，c，d 的大小順序是什麼，從1---n----這n個點更新一遍時   就一定可以得到AB的最短距離（在更新a，b，c，d過程中一定把AB連在了一起，不管先連的是 a - c 還是 b - d ）；

附思路程式碼：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int map[100][100];
int n,m;
void pri(int xx)//輸出每次更新xx點後的map 
{
	printf("\n     %d:\n",xx);
	for (int i=1;i<=n;i++)
	{
		for (int j=1;j<=n;j++)
		printf("%8d",map[i][j]);
		printf("\n");
	}
	printf("\n\n");
}
int main()
{
	n=4,m=5;
	for (int i=1;i<=n;i++)
	for (int j=1;j<=n;j++)
	if (i==j)
	map[i][j]=0;
	else
	map[i][j]=999999;
	int a,b,c;
	for (int i=0;i<m;i++)
	{
		scanf("%d%d%d",&a,&b,&c);
		map[a][b]=map[b][a]=min(c,map[a][b]);
	}
	
	pri(0);
	
	for (int k=1;k<=n;k++)//k 為i 和 j 點之間插入的點--然後判斷 ik + kj 與 ij  的長度大小--來決定是否更新ij的長度
	{
		for (int i=1;i<=n;i++)
		for (int j=1;j<=n;j++)
		map[i][j]=map[j][i]=min(map[i][j],map[i][k]+map[k][j]);
		pri(k);
	}
	return 0;
}
/*
 1 2 120
 1 3 20
 2 3 20
 2 4 20
 1 4 100
 */
 

題目是問從哪個人開始傳播最快--

求出每個人當源頭時到其他人的最長時間---誰的最長時間最少就從說開始---

Floyd 求 任意兩點的最短距

程式碼：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int map[120][120];
int n;
void floyd()
{
	for (int k=1;k<=n;k++)
	for (int i=1;i<=n;i++)
	for (int j=1;j<=n;j++)
	map[i][j]=min(map[i][j],map[i][k]+map[k][j]);
}
int main()
{
	while (scanf("%d",&n),n)
	{
		memset(map,0x3f3f3f,sizeof(map));
		for (int i=1;i<=n;i++)
		{
			int p,a,b;scanf("%d",&p);
			for (int j=0;j<p;j++)
			{
				scanf("%d%d",&a,&b);
				map[i][a]=min(map[i][a],b);
			}
		}
		floyd();
		int ii=-1,he=0xffffff;
		for (int i=1;i<=n;i++)
		{
			int ans=0;
			for (int j=1;j<=n;j++)
			{
				if (i==j) continue;
				ans=max(ans,map[i][j]);
			}
			if (ans<he)
			{
				he=ans;ii=i;
			}
		}
		printf("%d %d\n",ii,he);
	}
	return 0;
}