python的四大演算法及例項
什麼是演算法
1、什麼是演算法
演算法(algorithm):就是定義良好的計算過程,他取一個或一組的值為輸入,併產生出一個或一組值作為輸出。簡單來說演算法就是一系列的計算步驟,用來將輸入資料轉化成輸出結果。
mark:我們可以把所有的演算法想象為一本“菜譜”,特定的演算法比如菜譜中的的一道“老醋花生米”的製作流程,只要按照菜譜的要求製作老醋花生米,那麼誰都可以做出一道好吃的老醋花生米。so,這個做菜的步驟就可以理解為:“解決問題的步驟”
2、演算法的意義
假設計算機無限快,並且計算機儲存容器是免費的,我們還需要各種亂七八糟的演算法嗎?如果計算機無限快,那麼對於某一個問題來說,任何一個都可以解決他的正確方法都可以的!
當然,計算機可以做到很快,但是不能做到無限快,儲存也可以很便宜但是不能做到免費。
那麼問題就來了效率:解決同一個問題的各種不同演算法的效率常常相差非常大,這種效率上的差距的影響往往比硬體和軟體方面的差距還要大。
3、如何選擇演算法
第一首先要保證演算法的正確性
一個演算法對其每一個輸入的例項,都能輸出正確的結果並停止,則稱它是正確的,我們說一個正確的演算法解決了給定的計算問題。不正確的演算法對於某些輸入來說,可能根本不會停止,或者停止時給出的不是預期的結果。然而,與人們對不正確演算法的看法想反,如果這些演算法的錯誤率可以得到控制的話,它們有時候也是有用的。但是一般而言,我們還是僅關注正確的演算法!
第二分析演算法的時間複雜度
演算法的時間複雜度反映了程式執行時間隨輸入規模增長而增長的量級,在很大程度上能很好反映出演算法的好壞。
時間複雜度
1、什麼是時間複雜度
一個演算法花費的時間與演算法中語句的執行次數成正比例,哪個演算法中語句執行次數多,它花費時間就多。一個演算法中的語句執行次數稱為語句頻度或時間頻度。記為T(n)。
一般情況下,演算法中基本操作重複執行的次數是問題規模n的某個函式,用T(n)表示,若有某個輔助函式f(n),使得當n趨近於無窮大時,T(n)/f(n)的極限值為不等於零的常數,則稱f(n)是T(n)的同數量級函式。記作T(n)=O(f(n)),稱O(f(n)) 為演算法的漸進時間複雜度,簡稱時間複雜度。
2、時間複雜度的計算方法
一個演算法執行所耗費的時間,從理論上是不能算出來的,必須上機執行測試才能知道。但我們不可能也沒有必要對每個演算法都上機測試因為該方法有兩個缺陷:
- 想要對設計的演算法的執行效能進行測評,必須先依據演算法編寫相應的程式並實際執行。
- 所得時間的統計計算依賴於計算機的硬體、軟體等環境因素,有時候容易掩蓋演算法的本身優勢。
所以只需知道哪個演算法花費的時間多,哪個演算法花費的時間少就可以了。並且一個演算法花費的時間與演算法中語句的執行次數成正比例,哪個演算法中語句執行次數多,它花費時間就多。
一般情況下,演算法的基本操作重複執行的次數是模組n的某一個函式f(n),因此,演算法的時間複雜度記做:T(n)=O(f(n))。隨著模組n的增大,演算法執行的時間的增長率和f(n)的增長率成正比,所以f(n)越小,演算法的時間複雜度越低,演算法的效率越高。
在計算時間複雜度的時候,先找出演算法的基本操作,然後根據相應的各語句確定它的執行次數,再找出T(n)的同數量級(它的同數量級有以下:1,Log2n ,n ,nLog2n ,n的平方,n的三次方,2的n次方,n!),找出後,f(n)=該數量級,若T(n)/f(n)求極限可得到一常數c,則時間複雜度T(n)=O(f(n))。
3、常見的時間複雜度
常見的演算法時間複雜度由小到大依次為:
Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<Ο(n3)<…<Ο(2n)<Ο(n!)
求解演算法的時間複雜度的具體步驟:
- 找出演算法中的基本語句,演算法中執行最多的那條語句是基本語句,通常是最內層迴圈的迴圈體。
- 計算基本語句的執行次數的量級,保證最高次冪正確即可檢視他的增長率。
- 用大O幾號表示演算法的時間效能
如果演算法中包含鑲套的迴圈,則基本語句通常是最內層的迴圈體,如果演算法中包並列的迴圈,則將並列的迴圈時間複雜度相加,例如:

#!/usr/bin/env python #-*- coding:utf-8 -*- __author__ = 'luotianshuai' n = 100 for i in range(n): print(i) for i in range(n): ##每循i裡的一個元素,for迴圈內部巢狀的for迴圈就整個迴圈一次 for q in range(n): print(q)

第一個for迴圈的時間複雜度為Ο(n),第二個for迴圈的時間複雜度為Ο(n2),則整個演算法的時間複雜度為Ο(n+n2)=Ο(n2)。
Ο(1)表示基本語句的執行次數是一個常數,一般來說,只要演算法中不存在迴圈語句,其時間複雜度就是Ο(1)。
其中Ο(log2n)、Ο(n)、 Ο(nlog2n)、Ο(n2)和Ο(n3)稱為多項式時間,而Ο(2n)和Ο(n!)稱為指數時間,電腦科學家普遍認為前者(即多項式時間複雜度的演算法)是有效演算法,把這類問題稱為P(Polynomial,多項式)類問題,而把後者(即指數時間複雜度的演算法)稱為NP(Non-Deterministic Polynomial, 非確定多項式)問題。在選擇演算法的時候,優先選擇前者!
OK我懂對於沒有演算法基礎的同學,看起演算法來也很頭疼,但是這個是基礎和重點,不會演算法的開發不是一個合格的開發並且包括語言記得基礎也是需要好好整理的!加油吧~~ 咱們在一起看下時間複雜度的詳細說明吧
常見的時間複雜度示例
1、O(1)
#O(1) n = 100 sum = (1+n) * n/2 #執行一次 sum_1 = (n/2) - 10 #執行一次 sum_2 = n*4 - 10 + 8 /2 #執行一次
這個演算法的執行次數函式是f(n)=3。根據我們推導大O階的方法,第一步就是把常數項3改為1。在保留最高階項時發現,它根本沒有最高階項,所以這個演算法的時間複雜度為O(1)。
並且:如果演算法的執行時間不隨著問題規模n的增長而增加,及時演算法中有上千條語句,其執行的時間也不過是一個較大的常數。此類演算法的時間複雜度記作O(1)
2、O(n2)
n = 100 for i in range(n): #執行了n次 for q in range(n): #執行了n2 print(q) #執行了n2
解:T(n)=2n2+n+1 =O(n2)
一般情況下,對進迴圈語句只需考慮迴圈體中語句的執行次數,忽略該語句中步長加1、終值判別、控制轉移等成分,當有若干個迴圈語句時,演算法的時間複雜度是由巢狀層數最多的迴圈語句中最內層語句的頻度f(n)決定的。
3、O(n)

#O(n) n =100 a = 0 #執行一次 b = 1#執行一次 for i in range(n): #執行n次 s = a +b #執行n-1次 b =a #執行n-1次 a =s #執行n-1次

解:T(n)=2+n+3(n-1)=4n-1=O(n)
4、Ο(n3)
#O(n3) n = 100 for i in range(n):#執行了n次 for q in range(n):#執行了n^2 for e in range(n):#執行了n^3 print(e)#執行了n^3
簡單點來去最大值是:Ο(n3)
5、常用的演算法的時間複雜度和空間複雜度
| 排序法 | 平均時間 | 最差情況 | 穩定度 | 額外空間 | 備註 |
| 氣泡排序 | Ο(n2) | Ο(n2) | 穩定 | O(1) | n小時較好 |
| 交換排序 | Ο(n2) | Ο(n2) | 不穩定 | O(1) | n小時較好 |
| 選擇排序 | Ο(n2) | Ο(n2) | 不穩定 | O(1) | n小時較好 |
| 插入排序 | Ο(n2) | Ο(n2) | 穩定 | O(1) | 大部分已排序時較好 |
| 快速排序 | Ο(nlogn) | Ο(n2) | 不穩定 | Ο(nlogn) | n較大時較好 |
| 希爾排序(SHELL) | Ο(log2n) |
Ο(ns) 1<s<2 |
不穩定 | O(1) | s是所選分組 |
| 歸併排序 | Ο(log2n) | Ο(log2n) | 穩定 | O(1) | n大時較好 |
| 堆排序 | Ο(log2n) | Ο(log2n) | 不穩定 | O(1) | n大時較好 |
| 基數排序 | Ο(logRB) | Ο(logRB) | 穩定 | O(N) |
B是真數(0-9) R是基數(個十百) |
排序例項
排序演算法是在更復雜的演算法中的是一個構建基礎,所以先看下常用的排序。
1、氣泡排序
需求:
請按照從小到大對列表,進行排序==》:[69, 471, 106, 66, 149, 983, 160, 57, 792, 489, 764, 589, 909, 535, 972, 188, 866, 56, 243, 619]
思路:相鄰兩個值進行比較,將較大的值放在右側,依次比較!
原理圖:
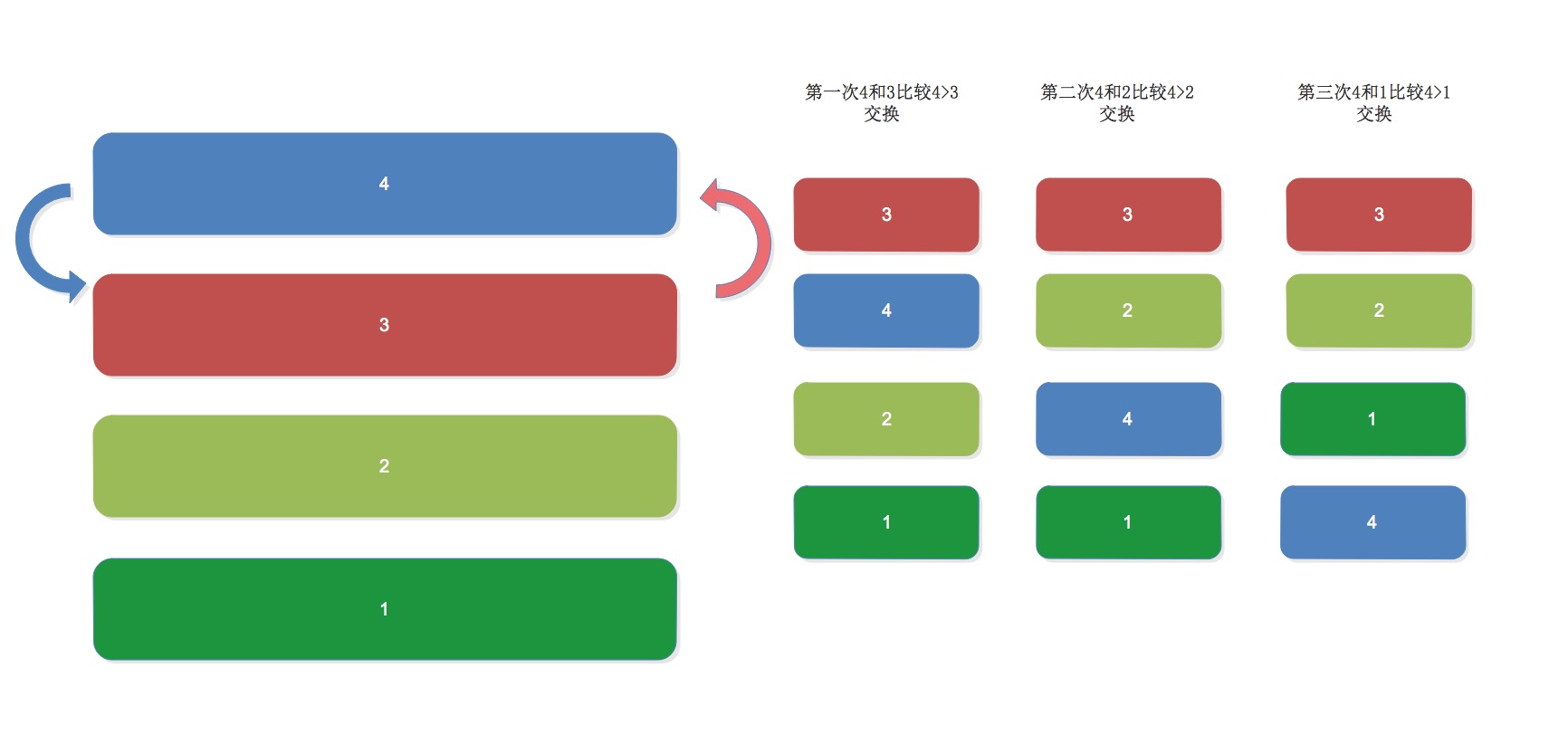
原理分析:
列表中有5個元素兩兩進行比較,如果左邊的值比右邊的值大,就用中間值進行迴圈替換!
既然這樣,我們還可以用一個迴圈把上面的迴圈進行在次迴圈,用表示式構造出內部迴圈!
程式碼實現:

#!/usr/bin/env python #-*- coding:utf-8 -*- __author__ = 'luotianshuai' import random maopao_list = [13, 22, 6, 99, 11] ''' 原理分析: 列表中有5個元素兩兩進行比較,如果左邊的值比右邊的值大,就用中間值進行迴圈替換! 既然這樣,我們還可以用一個迴圈把上面的迴圈進行在次迴圈,用表示式構造出內部迴圈! ''' def handler(array): for i in range(len(array)): for j in range(len(array)-1-i): ''' 這裡為什麼要減1,我們看下如果裡面有5個元素我們需要迴圈幾次?最後一個值和誰對比呢?對吧!所以需要減1 這裡為什麼減i?,這個i是迴圈的下標,如果我們迴圈了一次之後最後一隻值已經是最大的了還有必要再進行一次對比嗎?沒有必要~ ''' print('left:%d' % array[j],'right:%d' % array[j+1]) if array[j] > array[j+1]: tmp = array[j] array[j] = array[j+1] array[j+1] = tmp if __name__ == '__main__': handler(maopao_list) print(maopao_list)

時間複雜度說明看下他的程式碼複雜度會隨著N的增大而成指數型增長,並且根據判斷他時間複雜度為Ο(n2)
2、選擇排序
需求:
請按照從小到大對列表,進行排序==》:[69, 471, 106, 66, 149, 983, 160, 57, 792, 489, 764, 589, 909, 535, 972, 188, 866, 56, 243, 619]
思路:
第一次,從列表最左邊開始元素為array[0],往右迴圈,從右邊元素中找到小於array[0]的元素進行交換,直到右邊迴圈完之後。
第二次,左邊第一個元素現在是最小的了,就從array[1],和剩下的array[1:-1]內進行對比,依次進行對比!
對比:
他和氣泡排序的區別就是,氣泡排序是相鄰的兩兩做對比,但是選擇排序是左側的“對比元素”和右側的列表內值做對比!
原理圖:
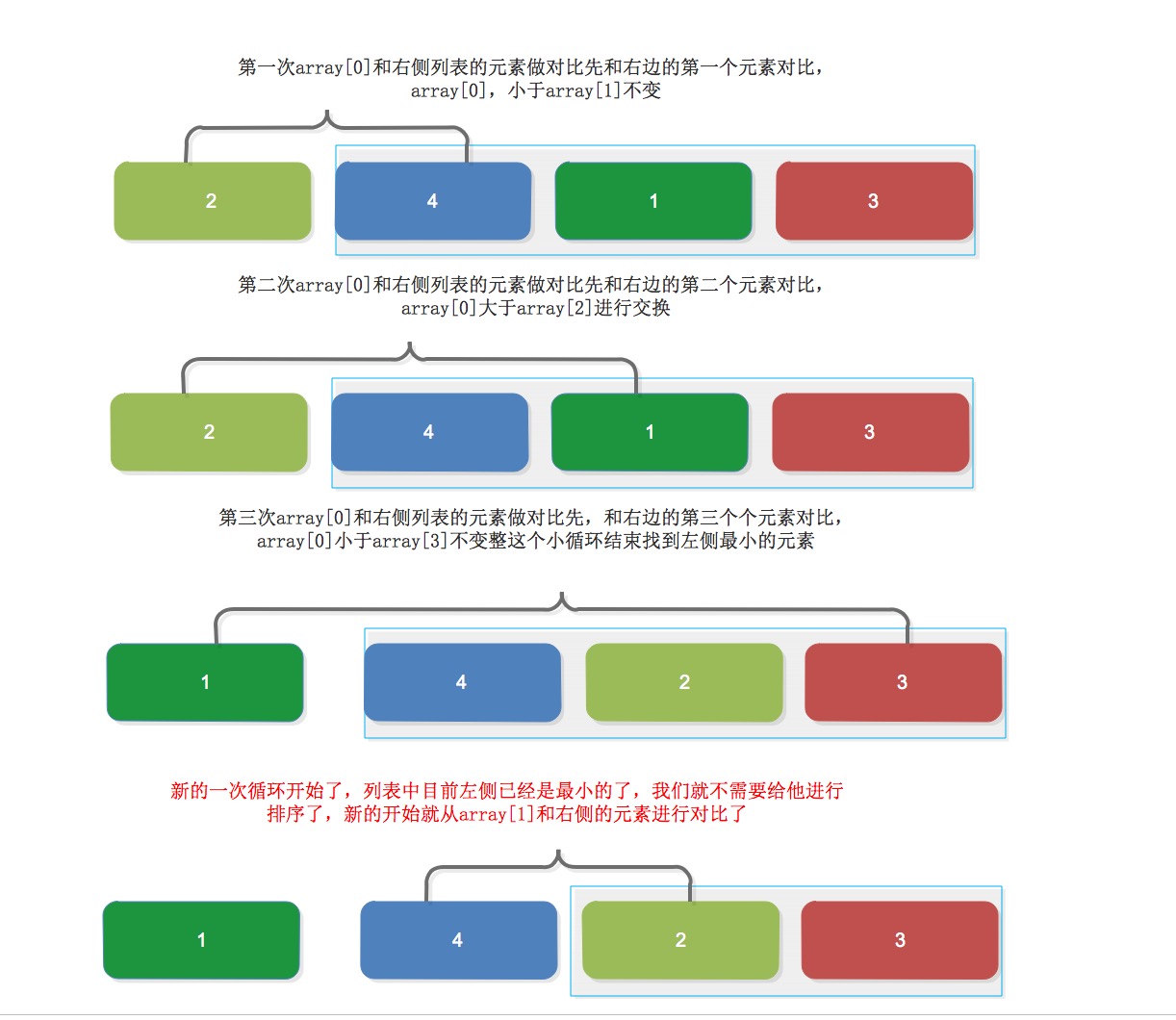
程式碼實現:

#!/usr/bin/env python #-*- coding:utf-8 -*- __author__ = 'luotianshuai' xuanze_list = [13, 22, 6, 99, 11] print(range(len(xuanze_list))) def handler(array): for i in range(len(array)): ''' 迴圈整個列表 ''' for j in range(i,len(array)): ''' 這裡的小迴圈裡,迴圈也是整個列表但是他的起始值是i,當這一個小迴圈完了之後最前面的肯定是已經排序好的 第二次的時候這個值是迴圈的第幾次的值比如第二次是1,那麼迴圈的起始值就是array[1] ''' if array[i] > array[j]: temp = array[i] array[i] = array[j] array[j] = temp # print(array) if __name__ == '__main__': handler(xuanze_list) print(xuanze_list)

選擇排序程式碼優化:

#!/usr/bin/env python #-*- coding:utf-8 -*- __author__ = 'luotianshuai' import random import time def handler(array): for i in range(len(array)): smallest_index = i #假設預設第一個值最小 for j in range(i,len(array)): if array[smallest_index] > array[j]: smallest_index = j #如果找到更小的,記錄更小元素的下標 ''' 小的迴圈結束後在交換,這樣整個小迴圈就之前的選擇排序來說,少了很多的替換過程,就只替換了一次!提升了速度 ''' tmp = array[i] array[i] = array[smallest_index] array[smallest_index] = tmp if __name__ == '__main__': array = [] old_time = time.time() for i in range(50000): array.append(random.randrange(1000000)) handler(array) print(array) print('Cost time is :',time.time() - old_time)

3、插入排序
需求:
請按照從小到大對列表,進行排序==》:[69, 471, 106, 66, 149, 983, 160, 57, 792, 489, 764, 589, 909, 535, 972, 188, 866, 56, 243, 619]
思路:
一個列表預設分為左側為排序好的,我們拿第一個元素舉例,他左邊的全是排序好的,他右側是沒有排序好的,如果右側的元素小於左側排序好的列表的元素就把他插入到合適的位置
原理圖:
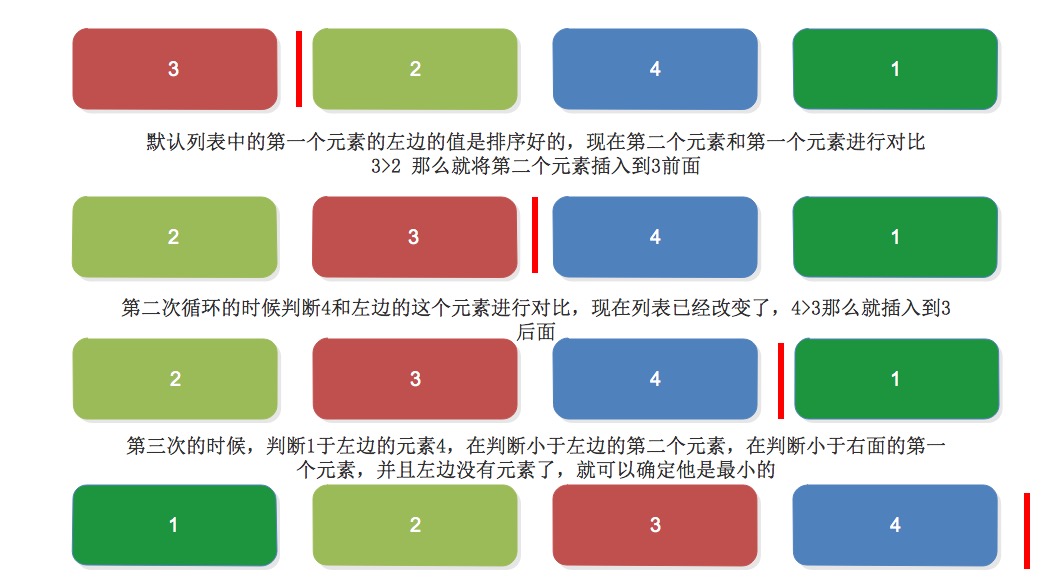
程式碼實現:

#!/usr/bin/env python #-*- coding:utf-8 -*- __author__ = 'luotianshuai' import random import time chaoru_list = [69, 471, 106, 66, 149, 983, 160, 57, 792, 489, 764, 589, 909, 535, 972, 188, 866, 56, 243, 619] def handler(array): for i in range(1,len(array)): position = i #剛開始往左邊走的第一個位置 current_val = array[i] #先把當前值存下來 while position > 0 and current_val < array[position -1]: ''' 這裡為什麼用while迴圈,咱們在判斷左邊的值得時候知道他有多少個值嗎?不知道,所以用while迴圈 什麼時候停下來呢?當左邊沒有值得時候,或者當他大於左邊的值得時候! ''' array[position] = array[position - 1] #如果whille條件成立把當前的值替換為他上一個值 ''' 比如一個列表: [3,2,4,1] 現在迴圈到 1了,他前面的元素已經迴圈完了 [2,3,4] 1 首先我們記錄下當前這個position的值 = 1 [2,3,4,4] 這樣,就出一個位置了 在對比前面的3,1比3小 [2,3,3,4] 在替換一下他們的值 在對比2 [2,2,3,4] 最後while不執行了在進行替換'array[position] = current_val #把值替換' ''' position -= 1 #當上面的條件都不成立的時候{左邊沒有值/左邊的值不比自己的值小} array[position] = current_val #把值替換 if __name__ == '__main__': handler(chaoru_list) print(chaoru_list) ''' array = []#[69, 471, 106, 66, 149, 983, 160, 57, 792, 489, 764, 589, 909, 535, 972, 188, 866, 56, 243, 619] old_time = time.time() for i in range(50000): array.append(random.randrange(1000000)) handler(array) print(array) print('Cost time is :',time.time() - old_time) '''

4、快速排序
設要排序的陣列是A[0]……A[N-1],首先任意選取一個數據(通常選用陣列的第一個數)作為關鍵資料,然後將所有比它小的數都放到它前面,所有比它大的數都放到它後面,這個過程稱為一趟快速排序。值得注意的是,快速排序不是一種穩定的排序演算法,也就是說,多個相同的值的相對位置也許會在演算法結束時產生變動.他的時間複雜度是:O(nlogn) ~Ο(n2)
排序示例:
假設使用者輸入瞭如下陣列:
建立變數i=0(指向第一個資料)[i所在位置紅色小旗子], j=5(指向最後一個數據)[j所在位置藍色小旗子], k=6(賦值為第一個資料的值)。
i=0 j=3 k=6
接著,開始第二次比較,這次要變成找比k大的了,而且要從前往後找了。遞加變數i,發現下標2的資料是第一個比k大的,於是用下標2的資料7和j指向的下標3的資料的6做交換,資料狀態變成下表:
i=2 j=3 k=6
稱上面兩次比較為一個迴圈。 接著,再遞減變數j,不斷重複進行上面的迴圈比較。 在本例中,我們進行一次迴圈,就發現i和j“碰頭”了:他們都指向了下標2。於是,第一遍比較結束。得到結果如下,凡是k(=6)左邊的數都比它小,凡是k右邊的數都比它大:如果i和j沒有碰頭的話,就遞加i找大的,還沒有,就再遞減j找小的,如此反覆,不斷迴圈。注意判斷和尋找是同時進行的。
然後,對k兩邊的資料,再分組分別進行上述的過程,直到不能再分組為止。 注意:第一遍快速排序不會直接得到最終結果,只會把比k大和比k小的數分到k的兩邊。為了得到最後結果,需要再次對下標2兩邊的陣列分別執行此步驟,然後再分解陣列,直到陣列不能再分解為止(只有一個數據),才能得到正確結果。程式碼實現:

#!/usr/bin/env python # -*- coding:utf-8 -*- # Author:luotianshuai import random import time def quick_sort(array,start,end): if start >= end: return k = array[start] left_flag = start right_flag = end while left_flag < right_flag: ''' left_flag = start 預設為0 right_flag = end 預設為傳來的列表總長度 當left_flag 小與right_flag的時候成立,說明左右兩邊的小旗子還沒有碰頭(為相同的值) ''' #右邊旗子 while left_flag < right_flag and array[right_flag] > k:#代表要繼續往左一移動小旗子 right_flag -= 1 ''' 如果上面的迴圈停止說明找到右邊比左邊的值小的數了,需要進行替換 ''' tmp = array[left_flag] array[left_flag] = array[right_flag] array[right_flag] = tmp #左邊旗子 while left_flag < right_flag and array[left_flag] <=相關推薦
python的四大演算法及例項
什麼是演算法 1、什麼是演算法 演算法(algorithm):就是定義良好的計算過程,他取一個或一組的值為輸入,併產生出一個或一組值作為輸出。簡單來說演算法就是一系列的計算步驟,用來將輸入資料轉化成輸出結果。 mark:我們可以把所有的演算法想象為一本“菜譜”,特定
貝葉斯演算法及例項python實現
目錄 計算過程: 貝葉斯簡介: 貝葉斯(約1701-1761) Thomas Bayes,英國數學家 貝葉斯方法源於他生前為解決一個“逆概”問題寫的一篇文章。 貝葉斯要解決的問題: 正向概率:假設袋子裡面有N個白球,M個黑球,你
各種基礎演算法及例項
一、貪心演算法 只根據當前情況做出最好的選擇,其最終結果可能不是最優解,也可以得到最優解的近似解。 貪心演算法遵循的兩個原則: 1、一旦做出選擇,不可以後悔。 2、最終結果可能不是最優解 二、分治法 將一個大問題分解成一個個小的問題,從上到下一層層解決,最後再進行合併,得到的
PageRank 演算法及例項分析
本文一部分是針對圖的PageRank 的實現,以及具體資料集的分析過程的記錄。 另一部分是BFS的實現,並記錄每一層的節點數。 資料集下載地址 soc-Slashdot0811 、 roadNet-CA 、 soc-LiveJournal1 1. java 實現程式碼 M
Python遺傳演算法程式碼例項講解
目錄 例項: 程式碼講解: 難度較大的程式碼: 全部程式碼: 例項: 求解函式的最大值y=xsin(10x)+xsin(2x),自變數取值:0--5,用Python畫出的影象如下 (注:此程式碼好像有一些感覺不對的地方,首先:沒有保留那些適應度
邏輯迴歸(logistics regression)演算法及例項
邏輯迴歸簡介 邏輯迴歸(Logistic Regression)是機器學習中的一種二分類模型(主要為二分類應用,Softmax 迴歸是直接對邏輯迴歸在多分類的推廣,即多元邏輯迴歸),由於演算法的簡單和高效,在實際中應用非常廣泛。 主要用途: 尋找危險因素
最短路徑之Dijkstra演算法及例項分析
Dijkstra演算法迪科斯徹演算法 Dijkstra演算法描述為:假設用帶權鄰接矩陣來表示帶權有向圖。首先引進一個輔助向量D,它的每個分量D[i]表示當前所找到的從始點v到每個終點Vi的最短路徑。它的初始狀態為:若兩頂點之間有弧,則D[i]為弧上的權值;否則置D[i]為無
Minimax演算法及例項分析
電腦科學中最有趣的事情之一就是編寫一個人機博弈的程式。有大量的例子,最出名的是編寫一個國際象棋的博弈機器。但不管是什麼遊戲,程式趨向於遵循一個被稱為Minimax演算法,伴隨著各種各樣的子演算
python實現PID演算法及測試
PID演算法實現 import time class PID: def __init__(self, P=0.2, I=0.0, D=0.0): self.Kp = P self.Ki = I self.Kd = D
Python使用Ctypes與C/C++ DLL檔案通訊過程介紹及例項分析
專案中可能會經常用到第三方庫,主要是出於程式效率考慮和節約開發時間避免重複造輪子。無論第三方庫開源與否,程式語言是否與當前專案一致,我們最終的目的是在當前程式設計環境中呼叫庫中的方法並得到結果或者藉助庫中的模組實現某種功能。這個過程會牽涉到很多東西,本篇文章將簡要的介紹一下該過程的一些問題。 1.背景 多
python 中join()函式strip() 函式和 split() 函式的詳解及例項
1、join()函式 Python中有join()和os.path.join()兩個函式,具體作用如下: join(): 連線字串陣列。將字串、元組、列表中的元素以指定的字元(分隔符)連線生成一個新的字串 語法: ‘sep’.join(seq) 引數說明 sep:分隔符。可以
python發郵件總結及例項說明,中文亂碼已解決(在最後一個模組)
python發郵件需要掌握兩個模組的用法,smtplib和email,這倆模組是python自帶的,只需import即可使用。smtplib模組主要負責傳送郵件,email模組主要負責構造郵件。 smtplib模組主要負責傳送郵件:是一個傳送郵件的動作,連線郵箱伺服器,登入郵箱,傳送郵件(有發件
Python遺傳演算法框架使用例項(二)多目標優化問題Geatpy for Python與Matlab的對比學習
在前面幾篇文章中,我們已經介紹了高效能Python遺傳和進化演算法框架——Geatpy的使用及一些案例。 本篇就一個多目標優化例項進行展開講述,並且與使用Matlab工具箱得到相近效果進行一些對比: Geatpy已於2018.09.20更新至1.0.6版本
KNN演算法及python實現
KNN演算法原理和python實現 K最近鄰(kNN,k-NearestNeighbor)分類演算法是資料探勘分類技術中最簡單的方法之一。 原理是:如果一個樣本在特徵空間中的k個最相鄰的樣本中的大多數屬於某一個類別,則該樣本也屬於這個類別,並具有這個類別上樣本的
Python實現凱撒密碼演算法及暴力破譯凱撒密碼演算法
一、凱撒加密法是什麼? 加密原理非常簡單,就是對字母表中的的每個字母,用它後面的第key個字母來代替。例如: 明文:meet me after the toga party 密文:PHHW PH
K-means演算法及python sklearn實現
目錄 前言 例項推演 K值的確定 輪廓係數 K-means演算法 前言 根據訓練樣本是否包含標籤資訊,機器學習可以分為監督學習和無監督學習。聚類演算法是典型的無監督學習,其訓練樣本中只包含樣本特徵,不包含樣本的標
基於圖的推薦演算法及Python實現(PersonalRank)
使用隨機遊走演算法PersonalRank實現基於圖的推薦。 二部圖 在推薦系統中,使用者行為資料可以表示成圖的形式,具體來說是二部圖。使用者的行為資料集由一個個(u,i)二元組組成,表示為使用者u對物品i產生過行為。本文中我們認為使用者對他產生過行為的物品的興
[Python模組]正則表示式 re模組的使用及例項
很喜歡Python教材中的這句格言: 有些人面臨問題時會想:“我知道, 我將使用正則表示式來解決這個問題.” 這讓他們面臨的問題變成了兩個. ---------Jamie Zawinski 正則表示式的確好用,但是複雜的模式難以閱讀和維護,與其把花在研究用正
Python四大流行排序演算法詳解--快速排序-氣泡排序-選擇排序-插入排序。
就作者而言使用Python經常用到的排序演算法就是快速排序、氣泡排序、選擇排序以及插入排序 就時間複雜度而言,快速排序是高階排序,查詢快速,時間複雜度為nlgn 而氣泡排序、選擇排序、插入排序則是比較低階的查詢演算法,時間複雜度為n**2 下面
KNN演算法原理及例項
文章目錄 KNN演算法原理 KNN演算法三要素 K值的選擇 距離度量的方式 分類決策規則 KNN演算法的計算過程 KNN演算法例項 KNN演算法的優點和缺點 KNN演算法原理 K最
