小數定律,大數定律,中心極限定理的理解和概括
(一)總述關係
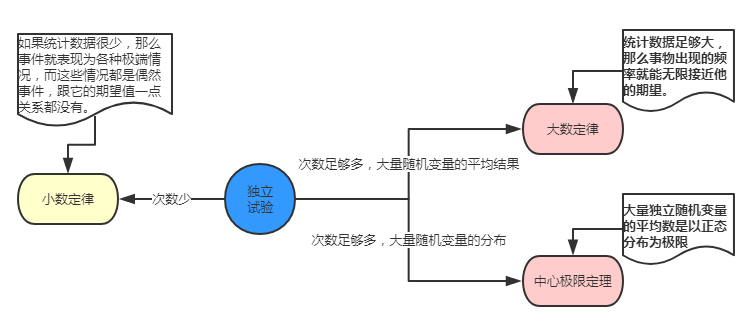
3者有些關係的,先描述下三者的關係,如圖:
(二)大數定律
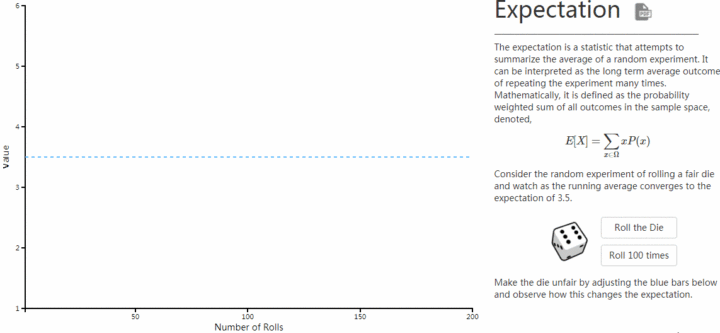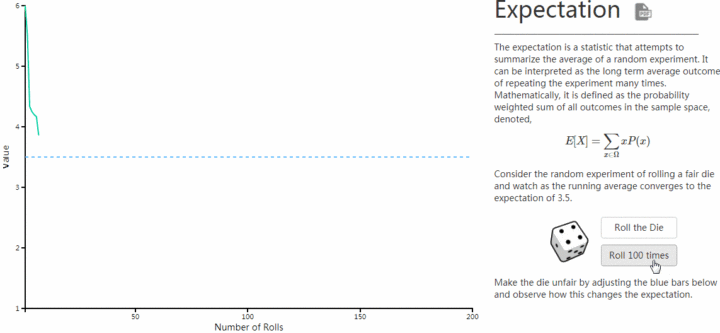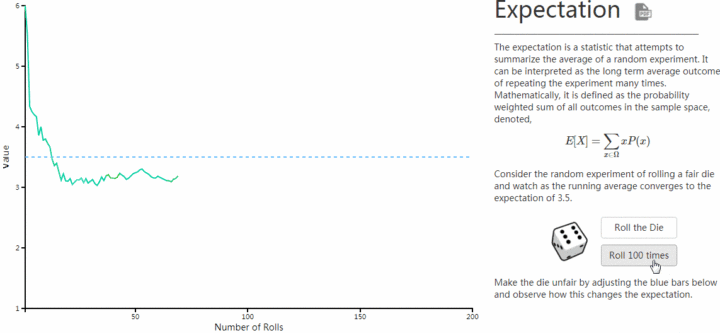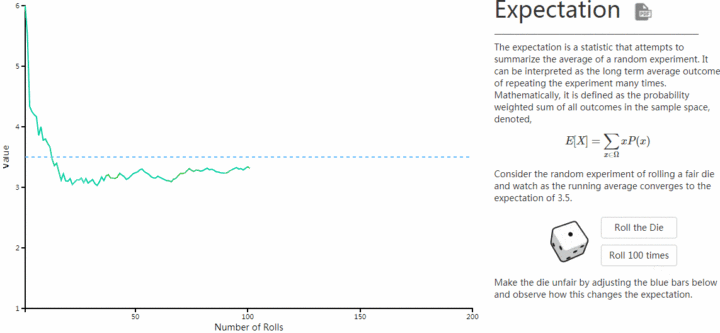
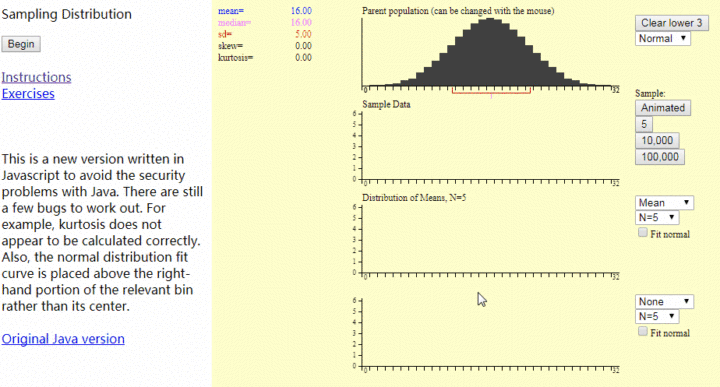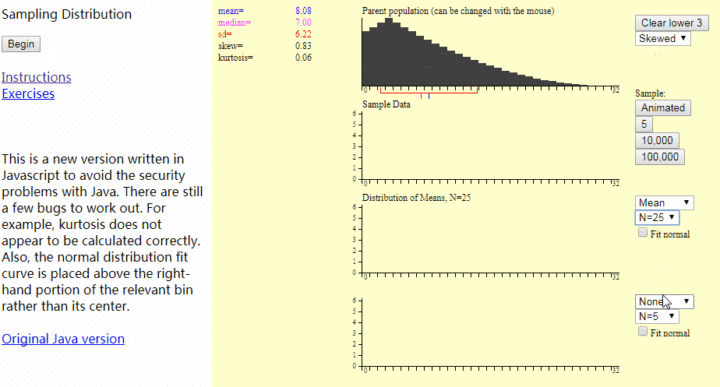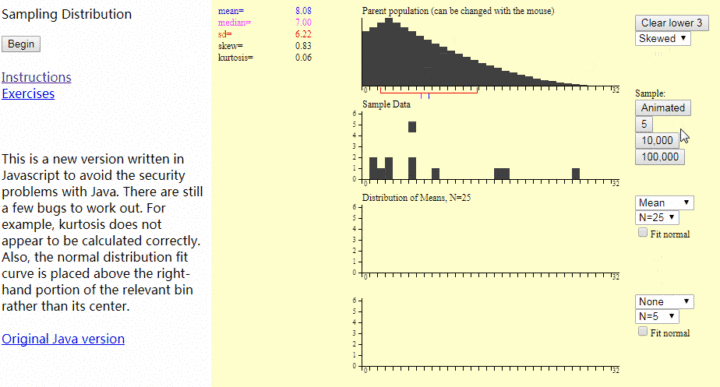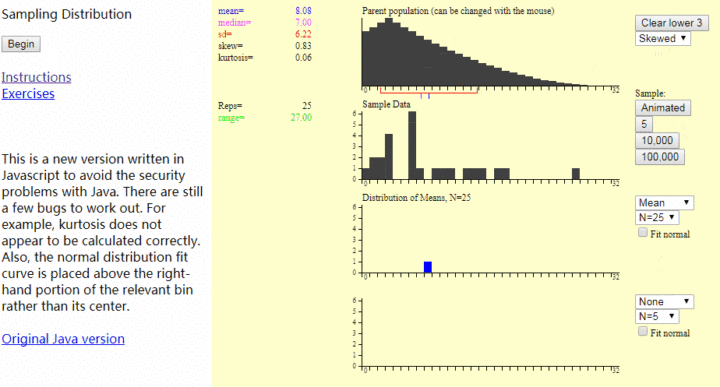
大數定律,動畫演示(下圖盜圖),描述的是擲骰子,骰子每一面出現的概率是1/6,次數少的時候小數定律,次數多的時候期望接近平均數3.5,
3.5 = 1 * 1/6 + 2 * 1/6 + 3 * 1/6 + 4 * 1/6 + 5 * 1/6 + 6 * 1/6
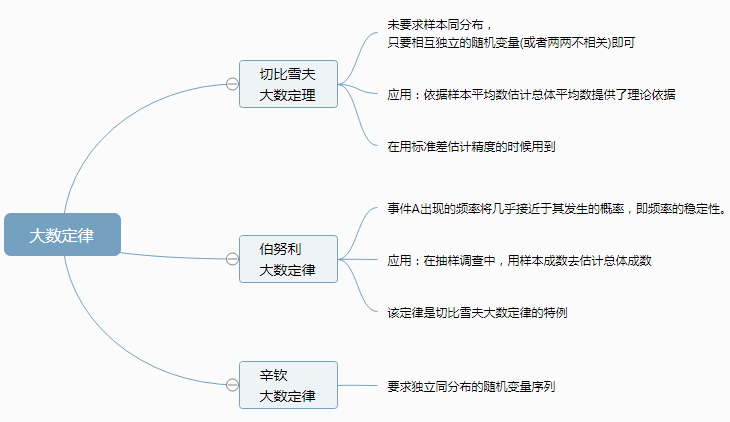
大數定律主要有三種,如下:
(三)中心極限定理
先概括下中心極限定理:
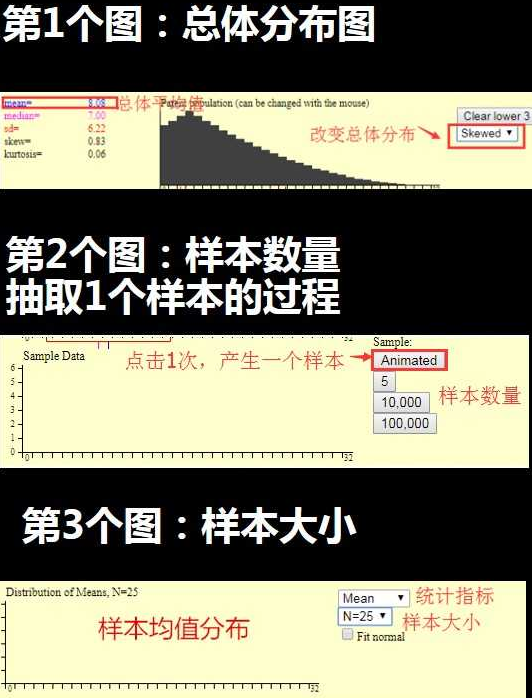
中心極限定理動畫演示:
解釋下:
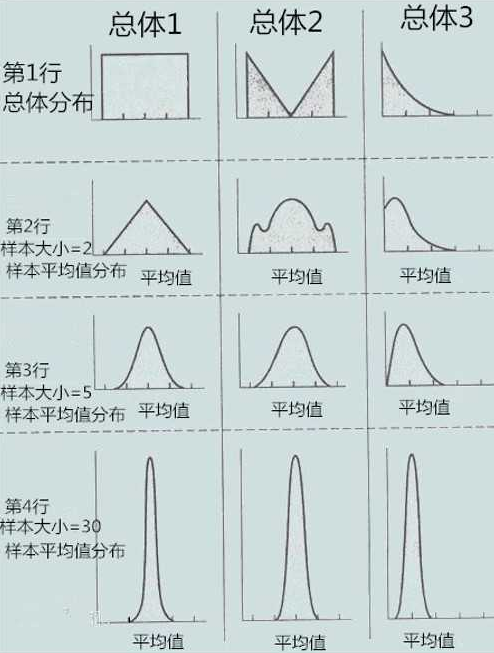
再拓展下:中心極限定律,不管總體是什麼分佈,任意一個總體的樣本平均值都會圍繞在總體的平均值周圍,並且呈正態分佈。
(下圖也是盜圖)
每天學習一點點,好了,手工幹活。
相關推薦
小數定律,大數定律,中心極限定理的理解和概括
(一)總述關係 3者有些關係的,先描述下三者的關係,如圖: (二)大數定律 大數定律,動畫演示(下圖盜圖),描述的是擲骰子,骰子每一面出現的概率是1/6,次數少的時候小數定律,次數多的時候期望接近平均數3.5, 3.5 = 1 * 1/6 + 2 * 1/6 + 3 *
基本極限定理(切比雪夫不等式,大數定律,中心極限定理)
人們在長期的實踐中發現,雖然個別事件在某次試驗中可能發生也可能不發生,但在大量重複實驗中卻呈現明顯的規律性,即一個隨機事件發生的頻率在某個固定數的附近搖擺,這就是所謂“頻率的穩定性”。 這裡介紹的就是概率論的理論基礎! 切比雪夫不等式 設隨機變數X的數學期望,方差,對任
中心極限定理 | central limit theorem | 大數定律 | law of large numbers
lar 導致 ber 品茶 question 出了 numbers .com 沒有 每個大學教材上都會提到這個定理,枯燥地給出了定義和公式,並沒有解釋來龍去脈,導致大多數人望而生畏,並沒有理解它的美。 《女士品茶》有感 待續~ 參考:怎樣理解和區分中
大數定律與中心極限定理
大數定律 定義: 設X1,X2,...,Xn,...X_1,X_2,...,X_n,...X1,X2,...,Xn,...為隨機變數序列,XXX為隨機變數,若對任意的正數ϵ\epsilonϵ有:l
機器學習學習筆記之二——大數定律、中心極限定理以及極大似然估計理解與用法
極大似然估計法常常出現在機器學習演算法的推導過程中,其使用場景或者說功能正是: 以已有樣本、已有公式去估計引數,最大可能的那個引數。 這樣來理解,極大似然估計法其實和機器學習演算法的目標都是一樣的。那麼極大似然估計法如何來用呢?
中心極限定理以及其和大數定律的區別
大數定律是說,n只要越來越大,我把這n個獨立同分布的數加起來去除以n得到的這個樣本均值(也是一個隨機變數)會依概率收斂到真值u,但是樣本均值的分佈是怎樣的我們不知道。 中心極限定理是說,n只要越來越大,這n個數的樣本均值會趨近於正態分佈,並且這個正態分佈以u為均值,sigma^2/n為方差。 綜上所述,這兩
詳細解釋大數定律+中心極限定理(三)
大數定律 大數定律就以嚴格的數學形式表現了隨機現象的一個性質:平穩結果的穩定性(或者說頻率的穩定性) 大數定律從理論上解決:用頻率近似代替概率的問題:P(A)≈nAnP(A)≈nAn;用樣本均值近似
概率論與數理統計--大數定律與中心極限定理
大數定律 切比雪夫不等式 隨機變數X的數學期望E(X)=a,方差為D(X)=σ2,對任意ϵ>0,有 P(|X−a|≥ϵ)≤σ2ϵ2 切比雪夫大數定律 隨機變數X1,X2,X3…..Xn,
中心極限定理與大數定律
Central limit theorem: We could be talking about melocular interactions and every time compound x interacts with compound y what m
【概率論與數理統計】小結6 - 大數定理與中心極限定理
tween 每次 研究 1-1 var 1.2 displays 一個 alt 註:這兩個定理可以說是概率論中最重要的兩個定理。也是由於中心極限定理的存在,使得正態分布從其他眾多分布中脫穎而出,成為應用最為廣泛的分布。這兩個定理在概率論的歷史上非常重要,因此對於它們的研究也
HDU 1316 (斐波那契數列,大數相加,大數比較大小)
n-n rmi mina -- leading else ring tput length 題目鏈接: http://acm.hdu.edu.cn/showproblem.php?pid=1316 Recall the definition of the Fibonacci
雲計算,大數據,人工智能三者有何關系?【轉】
能力 基於 永遠 箱子 理解 idc linux nts 相同 轉自:【http://cloud.idcquan.com/yjs/115806.shtml】原文:來源:今日頭條/領先網絡 2017-05-02 17:17 雲計算,大數據,和人工智能,最近火的不行不行的詞匯,
機器學習數學|大數定理中心極限定理矩估計
機器學習中的數學 覺得有用的話,歡迎一起討論相互學習~Follow Me 原創文章,如需轉載請保留出處 本部落格為七月線上鄒博老師機器學習數學課程學習筆記 概率密度/概率分佈
中心極限定理與大數定理理解
1.什麼是中心極限定理 有時候統計概率就像魔術一樣,能夠從少量資料中得出不可思議的強大結論。我們只需要對1000個美國人進行電話調查,就能去預測美國總統大選的得票數。 通過對為肯德基提供雞肉的加工廠生產的100塊雞肉進行病毒(沙門氏菌)檢測,就能得出這家工廠的所有肉類產品是否安全的結論。 這些“一概而論”的
使用C++類實現大數加法,大數減法,大數乘法
這寫的就是垃圾,多數還是抄的,沒有意思,為了應付作業啥的可以拿去試試,好多東西都算不對。希望後面看到的能自己寫,不然以後還要像我一樣,重新寫一遍。 效果截圖: #include <iostream> #include <string&g
中心極限定理和大數定理
統計學習方法介紹經驗風險的概念(相關筆記)時,提及大數定理,下面是個人對大數定理以及跟它有點相近的中心極限定理的理解: 1.大數定理的意思就是說當樣本數夠大的時候,樣本均值近似相應隨機變數的期望。舉個擲骰子的例子,擲n次骰子,記錄每次正面朝上的點數,最終可以算
hdu1002 ,大數相加,一點都不難,嘿嘿嘿
I have a very simple problem for you. Given two integers A and B, your job is to calculate the Sum of A + B. Input The first line of th
關於FFT的一些理解,以及如何手工計算FFT加深理解和驗證正確性
以及 手工 fft ges 系統 -1 nbsp 邏輯性 分享 總結缺少邏輯性和系統性,主要便於自己理解和記憶 關於FFT的一些理解,以及如何手工計算FFT加深理解和驗證正確性
小白學JAVA,與你們感同身受,JAVA---day5:關於多型的理解和分析。魯迅的一句話:總之歲月漫長,然而值得等待。
魯迅的一句話:總之歲月漫長,然而值得等待。 至於是不是他說的,就看大家的了。 /* 多型:事物存在的多種形態。 多型的前提: 1.要有繼承關係。 2.要有方法的重寫。 3.要有父類引用指向子類物件。 向上轉型和向下轉型: 1.父類引用指向子類物件 &nbs
中心極限定理的形象理解
中心極限定理是統計學中的一個重要定理,本文的目的是形象地講解中心極限定理,不列舉公式。 本篇部落格是基於猴子在知乎上的回答,進行的整理。非常感謝猴子的講解。 目錄 1 什麼是中心極限定理 有時候統計概率就像魔術一樣,能夠從少