序言

現代公鑰加密系統中，常用的加密演算法除了RSA還有離散對數加密和橢圓曲線加密。這兩者原理比較相似，在這裡一併介紹。

離散對數問題

我們在中學裡學的對數問題是指，

給定正實數a$a$和ax$a^x$，求x$x$。也就是計算x=logaax$x={\log }_a{a}^x$。

這是實數域上的對數問題，不是什麼難算的東西，隨便按一下計算器結果就出來了。

而離散對數問題是指這樣的問題：

給定素數p$p$和正整數g$g$，知道gxmodp$g^x\mathrm{mod}p$的值，求x$x$

對於符合特定條件的p$p$和g$g$，這個問題是很難解的，更準確地說，是沒有多項式時間的解法。

Diffie–Hellman金鑰交換

Diffie–Hellman金鑰交換（以下簡稱DH）是用於雙方在可能被竊聽環境下安全交換金鑰的一種方法。
演算法的安全性是由上面提到的離散對數難題保證。

具體演算法流程如下：

• 小紅和小明約定p$p$和g$g$的值
• 小紅生成私鑰x$x$，計算gxmodp$g^x\mathrm{mod}p$作為公鑰公佈出去
• 小明生成私鑰y$y$，計算gymodp$g^y\mathrm{mod}p$作為公鑰公佈出去
• 小紅得知gymodp$g^y\mathrm{mod}p$後，計算
  s=(gymodp)xmodp=(gy)xmodp=gxymodp$s=(g^y\mathrm{mod}p{)}^x\mathrm{mod}p=(g^y{)}^x\mathrm{mod}p=g^{xy}\mathrm{mod}p$
• 小明得到gxmodp$g^x\mathrm{mod}p$後，計算
  
  s=(gxmodp)ymodp=(gx)ymodp=gxymodp$s=(g^x\mathrm{mod}p{)}^y\mathrm{mod}p=(g^x{)}^y\mathrm{mod}p=g^{xy}\mathrm{mod}p$
• 雙方都得到了相同的金鑰的s$s$，交換完畢

上面的流程中，x$x$和y$y$始終由兩人自行保管的，第三方竊聽得到的只有p$p$、g$g$、gxmodp$g^x\mathrm{mod}p$和gymodp$g^y\mathrm{mod}p$這幾個值。
上面說過，離散對數是很難算的，所以第三方不能由這些資訊計算出x$x$或y$y$，也就沒辦法計算出金鑰s$s$了。

橢圓曲線

中學的時候我們學過圓錐曲線，比如橢圓、雙曲線和拋物線。因為描述這些曲線的方程都是二次方程，圓錐曲線又被稱為二次曲線。而橢圓曲線是則是由三次方程描述的一些曲線。更準確地說，橢圓曲線是由下面的方程描述的曲線：

y2=x3+ax+b其中4a3+27b2≠0$$y^2=x^3+ax+b其中4a^3+27b^2\ne 0$$
需要注意的是，橢圓曲線之所以叫“橢圓曲線”，是因為其曲線方程跟利用微積分計算橢圓周長的公式相似。實際上它的影象跟橢圓完全不搭邊。

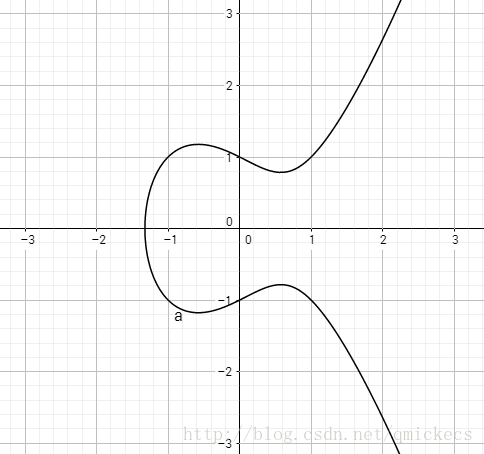
下圖是橢圓曲線y2=x3−x+1$y^2=x^3-x+1$的影象

橢圓曲線有這樣的兩個性質：

1. 關於X軸對稱
2. 畫一條直線跟橢圓曲線相交，它們最多有三個交點

橢圓曲線上的運算

由於橢圓曲線加密進行的運算實際上都是在橢圓曲線上進行的，所以接下來需要定義一些橢圓曲線上的運算。

必須注意的是，這裡把這些運算稱為“加法”和“乘法”僅僅是方便描述，他們跟平時認知的加法和乘法完全是兩碼事，完全可以給他們取其它名字（比如”乘法“和”冪運算“等）。

1. 首先定義座標系中距離X軸無窮遠點為橢圓曲線上的一個特殊點，稱為0點。
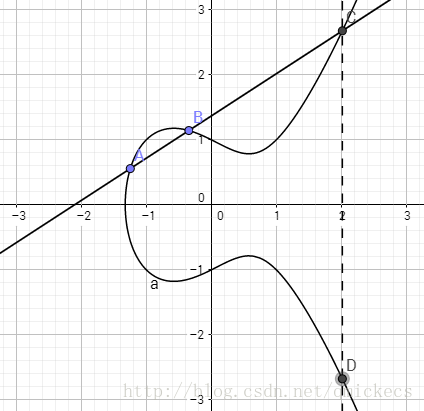
   那麼此時上述第二條性質可以加強為：過曲線上任意兩點（可重合）的直線必定與曲線相交於第三點。

2. 然後定義橢圓曲線上點的加法。設橢圓曲線上有兩點，A和B點，那麼作過這兩點的直線與該曲線相交於第三點（C點），然後關於X軸對稱得到D點，則D為這兩個點的和，記作D=A+B$D=A+B$。很明顯，D點也在該曲線上。所以橢圓曲線上兩點之和也是曲線上的點。
   

   特別地，如果兩點重合，則作橢圓曲線在A點處的切線，與曲線相交於第二點（B點），然後關於X軸對稱得到C點，則C點為A點與自身的和，記作C=A+A$C=A+A$
   

   那麼關於這個加法，我們可以得到以下結論：

   • A+B=B+A$A+B=B+A$
     也就是橢圓曲線上的加法滿足交換律。

   • A+0=A$A+0=A$
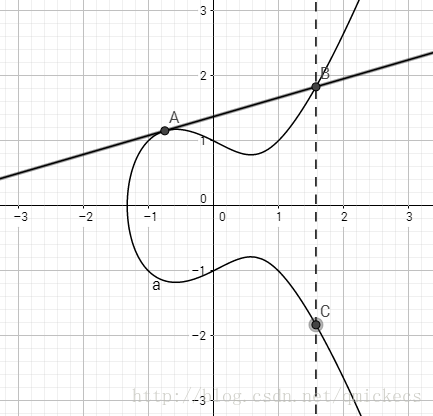
     因為0點是無窮遠點，所以過A點與0點的直線是垂直於X軸的，它與曲線相交於另一點B點，那麼B點關於X軸對稱的點就是A點，即A點為A點和0點之和。
     

     相關推薦

     離散對數和橢圓曲線加密原理

     序言 現代公鑰加密系統中，常用的加密演算法除了RSA還有離散對數加密和橢圓曲線加密。這兩者原理比較相似，在這裡一併介紹。 離散對數問題 我們在中學裡學的對數問題是指， 給定正實數aa和axax，求xx。也就是計算x=logaaxx=lo

     比特幣錢包地址的概念以及SHA256和橢圓曲線乘法加密演算法的詳解

     比特幣錢包，金鑰，地址 錢包就是金鑰所在之處，錢包是私鑰的容器，通過有序檔案或者簡單的資料庫實現或者用原有的私鑰通過單向雜湊函式生成每一個新的私鑰，並將新的金鑰順序連線。 比特幣錢包包含的是私鑰而不是比特幣，一個使用者可以有一個或者多個私鑰的錢包，錢包中含有成對的私鑰和公鑰

     如何給小學生講清楚ECC橢圓曲線加密

     對於RSA這套公私鑰加密的思路，我以為我挺明白的，運用的嫻熟自如。 當然現在RSA用的不多，而是基於ECC曲線來做簽名驗籤，最大名鼎鼎的莫過於比特幣。 可是前兩天和別人講程式碼，被問了ECC為什麼可以用來做驗籤，發現自己講不清楚。 所以做了點功課，來把這個問題講清楚。 首先我們跳過ECC曲線是個啥這個話題，這

     ECC橢圓曲線加密演算法

     橢圓曲線加密也是一種公鑰加密演算法，和RSA與離散對數一樣，它也是基於一個數學求解的難題，並且它的難度比RSA和離散對數都要大，它基於的數字難題就是求取定義在橢圓曲線上的離散對數的求取難題，對於這個難題的描述比大數分解和離散對數要稍微複雜一些，不過它也還算比較形

     簡單橢圓曲線加密演算法（ECC)示例（MATLAB實現）

     摘要 本文主要是使用MATLAB演示橢圓曲線加密演算法（ECC）的加密/解密過程，內容包括金鑰、公鑰生成，以及通過加密並解密一個簡單數字的過程來描述其使用方法。 本文實際是對以下兩篇文章的一個MATLAB實現，並且提供了兩個實用的MATLAB工具函式以便在閱

     橢圓曲線加密演算法

       橢圓曲線密碼學（Elliptic curve cryptography），簡稱ECC，是一種建立公開金鑰加密的演算法，也就是非對稱加密。類似的還有RSA，ElGamal演算法等。ECC被公認為在給定金鑰長度下最安全的加密演算法。比特幣中的公私鑰生成以及簽名演算法ECDSA都是基於ECC的。下面簡單介紹E

     橢圓曲線加密學習的菜鳥入門

     橢圓曲線：一個更好的trapdoor構件 橢圓曲線是滿足特定數學等式的點的集合。橢圓曲線的方程像如下的樣子：   它的影象：   還有其他形式的橢圓曲線的表達形式，但是一般的橢圓曲線方程，一個變數為2階，一個變數為3階。它有一些好的屬性用於加密。 1.奇怪的對稱性 它是水平

     區塊鏈中的密碼學（三）-橢圓曲線加密算法分析

     自己的 愛好 focus 一個數 如果 imp 變化 關註 bre 在目前密碼學的非對稱加密算法中，RSA算法依然是一種主流，但是隨著比特幣中對於一種之前不太流行的算法：橢圓加密算法（ECC）的成功應用後，這種算法得到了很大的關註和普及。有一種說法是中本聰不信任RSA算法，

     c++ 簡單的實現橢圓曲線加密演算法

     橢圓曲線演算法 橢圓曲線密碼體制來源於對橢圓曲線的研究，所謂橢圓曲線指的是由韋爾斯特拉斯（Weierstrass）方程： y2+a1xy+a3y=x3+a2x2+a4x+a6 (1) 所確定的平面曲線。其中係數ai(I=1,2,…,6)定義在某個域上，可以是有理數域、實數域

     什麼是橢圓曲線加密（ECC）？

     轉載自http://8btc.com/article-138-1.html，一次沒看明白記錄下來多看幾次。 比特幣使用橢圓曲線演算法生成公鑰和私鑰，選擇的是secp256k1曲線。與RSA（Ron Rivest，Adi Shamir，Len Adleman三位

     橢圓曲線加密演算法SM2在Android用Java呼叫實現

             SM2基於ECC，ECC（Elliptic Curves Cryptography）加密演算法是一種公鑰加密演算法，與主流的RSA演算法相比，ECC演算法可以使用較短的金鑰達到相同的安全程度。近年來，人們對ECC的認識已經不再處於研究階段，開始逐步進入實際應用

     python實現的橢圓曲線加密

     col sha2 -s emp for in spa 屬於 質數分解 app 我也看得雲裏霧裏， 但是ECC和RSA並列為非對稱加密雙雄， 還是很有必要了解一下的。 RSA是用質數分解，ECC是用離散的橢圓方程解，安全度更高。 而且，這個ECC的加法乘法規則，和普通

     橢圓曲線加密演算法的證書

     網上介紹openssl建立RSA演算法的證書很多，但是建立橢圓曲線證書的少。即使這些介紹橢圓曲線的，都不對，創建出來的證書無法使用。 最終基於該開源工具成功建立了： http://sourceforge.net/projects/xca/

     關於密碼中的RSA演算法和ecc(橢圓曲線)演算法加密過程是怎樣的?

     作者：Kalafinaian 連結：https://www.zhihu.com/question/26662683/answer/325511510 來源：知乎 著作權歸作者所有。商業轉載請聯絡作者獲得授權，非商業轉載請註明出處。   Oblivious 何処へ行くの

     區塊鏈教程區塊鏈資訊保安3橢圓曲線加解密及簽名演算法的技術原理一

     　　區塊鏈教程區塊鏈資訊保安3橢圓曲線加解密及簽名演算法的技術原理一，2018年下半年，區塊鏈行業正逐漸褪去發展之初的浮躁、迴歸理性，表面上看相關人才需求與身價似乎正在回落。但事實上，正是初期泡沫的漸退，讓人們更多的關注點放在了區塊鏈真正的技術之上。 橢圓曲線加解密及簽名演算法的技術原理及其Go語言實現

     區塊鏈教程區塊鏈信息安全3橢圓曲線加解密及簽名算法的技術原理一

     rsa 回歸 語言 集合 規則 區塊 連續 rsa加密 對稱加密 區塊鏈教程區塊鏈信息安全3橢圓曲線加解密及簽名算法的技術原理一，2018年下半年，區塊鏈行業正逐漸褪去發展之初的浮躁、回歸理性，表面上看相關人才需求與身價似乎正在回落。但事實上，正是初期泡沫的漸退，讓人們更多

     ECC橢圓曲線、ECDSA簽名驗籤和ECIES加解密

     ECC橢圓曲線詳解前言ECC英文全稱"Ellipse Curve Cryptography"，與傳統的基於大質數因子分解困難性的加密方法不同，ECC通過橢圓曲線方程式的性質產生金鑰ECC164位的金鑰產生一個安全級，相當於RSA 1024位金鑰提供的保密強度，而且計算量較小，

     使用橢圓曲線進行加密解密

     來源：http://blog.csdn.net/lff0305/article/details/49492711 JDK中自帶了橢圓曲線的簽名，但是沒有實現橢圓曲線的加密解密。不過bouncycastle庫實現了，下面的程式碼需要bouncycastle庫。 需要做

     非對稱加密、ssl和tls的工作原理

     假設網際網路上的A和B要進行安全的通訊，為了防止訊息被別人截獲以及篡改，它們會使用一個共同的暗號來對要傳送的訊息及接受的訊息進行加密解密，這也就是大家經常提到的對稱加密機制，其中暗號與諜戰中的密碼本大同小異。 對稱加密似乎完美的解決了安全通訊的問題，前提是通訊的暗號或

     MD5加密原理和Java實現

     MD5加密演算法為現在應用最廣泛的雜湊演算法之一，該演算法廣泛應用於網際網路網站的使用者檔案加密，能夠將使用者密碼加密為128位的長整數。資料庫並不明文儲存使用者密碼，而是在使用者登入時將輸入密碼字串進行MD5加密，與資料庫中所儲存的MD5值匹配，從而降低密碼資料庫被盜取