這個DEMO是參考了TensorFlow.js官網的教程，融合了一些自己的實現。

具體效果是怎麼樣的呢？少廢話，先看東西：

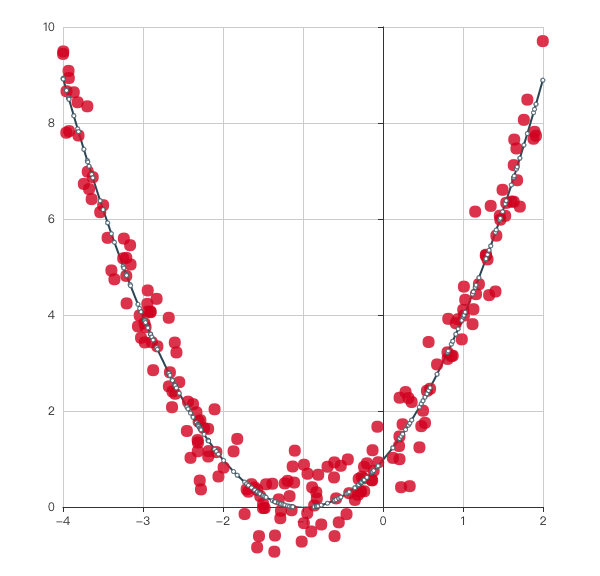
這是一個二次函式曲線的擬合，效果我個人覺得還可以。

為了實現這個效果，首先我們得有要有資料，不然我們擬合什麼？資料就是下圖所示的這些散點。

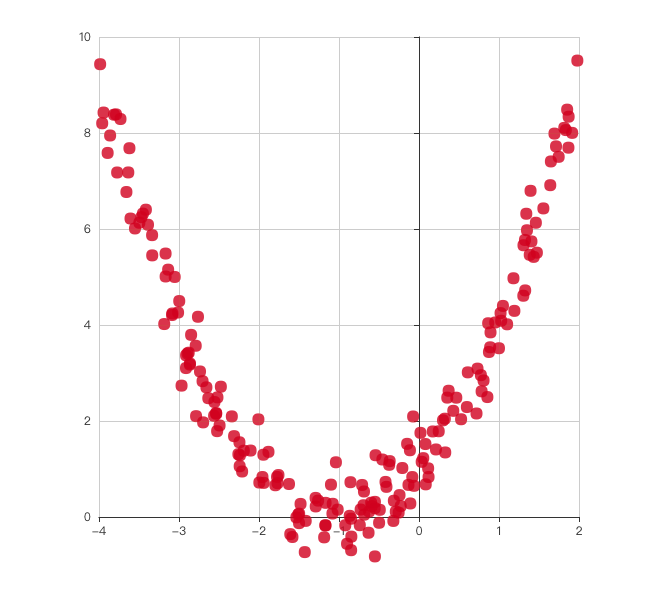
為了巧婦能有米來炊，我們首先得要實現一個產生資料的函式。

function generateData(numPoints, coeff, sigma = 0.5) {
  return tf.tidy(() => {
    const [a, b, c] = [
      tf.scalar(coeff.a),
      tf.
 
scalar(coeff.b),
      tf.scalar(coeff.c)
    ];
  
    const xs = tf.randomUniform([numPoints], -4, 2);
    const ys = a.mul(xs.pow(tf.scalar(2, 'int32')))
      .add(b.mul(xs))
      .add(c)
      //新增噪聲
      .add(tf.randomNormal([numPoints], 0, sigma));
    
    /*
    //資料歸一化
    const ymin = ys.min();
    const ymax = ys.max();
    const yrange = ymax.sub(ymin);
    const ysNormalized = ys.sub(ymin).div(yrange);
    */
 

    
    return {
      xs,
      ys: ys
    };
  })
}

我們首先是要拿到你所要擬合的函式的係數，本例中所要擬合的函式方程是$y=x^2+2x+1$,所以$a=1,b=2,c=1$。

然後我們使用tf.randomUniform方法產生指定數量，指定範圍且均勻分佈的點的X座標。

接下來我們就要通過計算得出點的Y座標，如下面程式碼所示。

const ys = a.mul(xs.pow(tf.scalar(2, 'int32')))
      .add(b.mul(xs)
 
)
      .add(c)

到這裡，y座標已經被計算出來了，然而我們還需要為它們新增噪聲，不然我們就沒有什麼好擬合的了。

.add(tf.randomNormal([numPoints], 0, sigma));

tf.randomNormal和上面的tf.randomUniform一樣都是產生隨機數，不同在於tf.randomNormal生成的資料是正態分佈的。

我註釋掉的那段程式碼是對y值進行歸一化操作，實際上歸一化能夠提高效率，我只是為了資料看起來更符合直覺去掉了它，在實際應用中還是最好保留。

資料產生完了，下面就是重頭戲–模型的構造與訓練。

1.宣告變數

首先，我們要宣告一些變數（就是函式的係數），用以存放最終訓練完成後擬合出的函式係數。不過一開始我們只是給他們賦成隨機數。

const a = tf.varible(tf.scalar(Math.random()));
const b = tf.varible(tf.scalar(Math.random()));
const c = tf.varible(tf.scalar(Math.random()));

2.構建一個模型

一個模型其實就是一個函式，你給出一個輸入，模型便會給你一個你期望中的結果。那麼在本例中，模型便是要計算$y=x^2+2x+1$。

function predict(x) {
  return tf.tidy(() => {
    return a.mul(x.pow(tf.scalar(2, 'int32'))) 
      .add(b.mul(x))
      .add(c);
  });
}

如果你寫到這裡就直接執行的話，那麼你得到的散點跟繪製出的曲線根本沒有什麼關係，原因很簡單，因為在這個時候模型的係數依然還是隨機數。所以我們還需要對模型進行訓練。

3.訓練模型

• 定義損失函式:
  在這個例子中，我使用了均方誤差作為損失函式。程式碼如下

function loss(prediction, labels) {
  const squareMeanError = prediction.sub(labels).square().mean();
  return squareMeanError;
}

• 定義優化器：
  在這個例子裡面，我使用了SGD（隨機梯度下降）。TensorFlow.js提供了簡便的方法來實現SGD，我們就不用操心要自己來寫許多繁雜的數學計算了。在這裡，我使用了tf.train.sgd，這個方法需要一個learning rate 作為引數。

learning rate 控制了當改進預測值時需要對函式係數做出的變動大小。一個低的learning rate 將會使學習過程變得更緩慢，因為需要更多的迭代次數。一個大的learning rate 雖然能使學習過程變快，但是可能導致模型總在正確值附近搖擺。

const learningRate = 0.5;
const optimizer = tf.train.sgd(learningRate);

• 定義訓練迭代
  我們定義完了損失函式和優化器之後，我們就可以構建訓練的迭代過程了。這個過程就是迭代的執行隨機梯度下降來改進模型的引數從而最小化損失。

async function train(xs, ys, numIterations) {
  for (let iter = 0; iter < numIterations; iter++) {
    optimizer.minimize(() => {
      const pred = predict(xs);
      return loss(pred, ys);
    });
    await tf.nextFrame();
  }
}

引數中的xs,ys就是上面生成的資料，numIterations就是迭代次數。
在for迴圈中，我們執行優化器的minimize方法。

minimize方法接受一個函式作為引數，這個函式需要做兩件事：

1. 使用predict（也就是模型）為所有的x都計算出y值。
2. 返回這些y值的均方誤差（使用前面定義的loss函式計算）

minimize方法將會自動的修改被這個函式呼叫的變數（也就是函式引數），目的是最小化損失。
訓練的迭代過程執行完後，a、b、c將會變為模型經過numIteration次隨機梯度下降後所學習到的值。

最後執行就能看到文章開頭圖片的效果了，DEMO完整的程式碼，在這裡。