原理

線性迴歸，原理很簡單，就是擬合一條直線使得損失最小，損失可以有很多種，比如平方和最小等等；

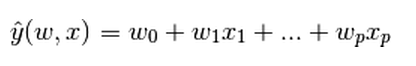
y是輸出，x是輸入，輸出是輸入的一個線性組合。

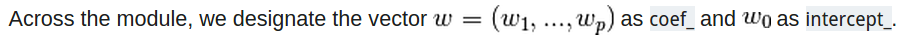
係數矩陣就是coef，截距就是intercept；

例子：

我們的輸入和輸出是numpy的ndarray，輸入是類似於列向量的，輸出類似於行向量，看它們各自的shape就是：
輸出：y.shape ——>(1,)
輸入：x.shape——->(m,1) #m是一個數字
大家記得不要把形式弄錯啦，不然可就走不起來了；

下面是個最簡單的例子：

>>> from sklearn import
 
 linear_model #匯入線性模型
>>> clf = linear_model.LinearRegression() #使用線性迴歸
>>> clf.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2]) #對輸入和輸出進行一次fit，訓練出一個模型
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> clf.coef_  #係數矩陣
array([ 0.5,  0.5])

稍微複雜點的例子：

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model

# 讀取自帶的diabete資料集
 

diabetes = datasets.load_diabetes()


# 使用其中的一個feature
diabetes_X = diabetes.data[:, np.newaxis, 2]

# 將資料集分割成training set和test set
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]

# 將目標（y值）分割成training set和test set
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20
 
:]

# 使用線性迴歸
regr = linear_model.LinearRegression()

# 進行training set和test set的fit，即是訓練的過程
regr.fit(diabetes_X_train, diabetes_y_train)

# 打印出相關係數和截距等資訊
print('Coefficients: \n', regr.coef_)
# The mean square error
print("Residual sum of squares: %.2f"
      % np.mean((regr.predict(diabetes_X_test) - diabetes_y_test) ** 2))
# Explained variance score: 1 is perfect prediction
print('Variance score: %.2f' % regr.score(diabetes_X_test, diabetes_y_test))

# 使用pyplot畫圖
plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')
plt.plot(diabetes_X_test, regr.predict(diabetes_X_test), color='blue',
         linewidth=3)

plt.xticks(())
plt.yticks(())

plt.show()

可以看出，使用還是很簡單的，就是準備好資料集：

regr = linear_model.LinearRegression() #使用線性迴歸
regr.fit(diabetes_X_train, diabetes_y_train) #訓練獲得一個model
regr.predict(diabetes_X_test) # 預測
regr.score(diabetes_X_test, diabetes_y_test) # 獲取模型的score值

OK，就到這，下次繼續！