用於求最近公共祖先(LCA)的 Tarjan演算法–以POJ1986為例(轉)
給定有向無環圖(就是樹,不一定有沒有根),給定點U,V,找出點R,保證點R是U,V的公共祖先,且深度最深;或者理解為R離這兩個點的距離之和最小.如何找出R呢?
最一般的演算法是DFS(DFS本是深度優先搜尋,在這裡姑且把深度優先遍歷也叫做DFS,其實是一種不嚴謹的說法).先看一道赤裸裸的LCA:POJ 1330 Nearest Common Ancestors 這道題給出了根節點,還保證”the first integer is the parent node of the second integer”(輸入第一個數是第二個數的祖先),這是赤裸裸的LCA,演算法很簡單,從根節點DFS一遍,按DFS層數k給每個節點標上深度deep[i]=k.然後從U點DFS到V點,找到後回溯,在回溯的路徑上找到一個deep[i]最小的節點即為LCA.
強大的LCA Tarjan演算法能在一遍遍歷後應答全部的LCA查詢,時間複雜的約為Θ(N)
有人說POJ1330是一道LCA Tarjan,在我看來完全不是,LCA Tarjan演算法的用途是處理大量請求,如果只有幾個(POJ1330每個Case只有一個)詢問大可不必寫Tarjan演算法,不過,1986的程式設計難度高,如果只是想先學LCA Tarjan, 用1330驗證正確性也不是不可以.
LCA Tarjan演算法
輸入格式大意:
第1行:節點數N,邊數M
第2…M+1行:起始節點,目標節點,路徑長度,方向(無意義字元,本題直接忽略)
第M+2行:詢問個數K(1 <= K <= 10,000)
第N+3…2+M+K行:查詢 U,V
這道題用DFS做的時間複雜度為Θ(K×N)
首先,LCA Tarjan 是一種離線演算法,要求一次讀入所有詢問,一次性輸出,這正是LCA Tarjan 演算法的精髓
以下大量引用Sideman神牛的話:
LCA Tarjan基本框架:
先用隨便一種資料結構(連結串列就行),把關於某個點的所有詢問標在節點上,保證遍歷到一個點,能得到所有有關這個節點LCA 查詢
建立並查集.注意:這個並查集只可以把葉子節點併到根節點,即getf(x)得到的總是x的祖先
深度優先遍歷整棵樹,用一個Visited陣列標記遍歷過的節點,每遍歷到一個節點將Visite[i]設成True 處理關於這個節點(不妨設為A)的詢問,若另一節點(設為B)的Visited[B]==True,則迴應這個詢問,這個詢問的結果就是getf(B). 否則什麼都不做
當A所有子樹都已經遍歷過之後,將這個節點用並查集併到他的父節點(其實這一步應該說當葉子節點回溯回來之後將葉子節點併到自己,並DFS另一子樹)
當一顆子樹遍歷完時,這棵子樹的內部查詢(即LCA在這棵子樹內部)都已經處理了
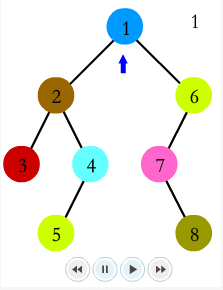
LCA Tarjan 演算法演示
假設我們要查詢
(3,4) (3,5) (5,6) (6,7) (1,8)
以(3,4)為例,說下Tarjan是如何工作的:
當DFS到3時,發現查詢(3,4),檢視4是否被DFS過,顯然這是不可能的.
回溯到2,將3併入2.
DFS節點4,發現查詢(3,4),檢視visited[3],發現被訪問過,應答查詢(3,4),應答getf(3)=2;
LCA Tarjan 演算法遍歷每個點一遍,處理所有詢問,時間複雜度為Θ(N+2M)
下面貼出POJ1986的題解
首先LCA Tarjan 沒的說,但是題目要求迴應的不是LCA,而是兩節點間距離,可以這樣做
改造並查集,定義dis[i]陣列,儲存i到getf(i)的距離
定義Deep[i]陣列,表示i節點的深度,DFS時順便更新depp[i];
定義Sum[I]陣列,表示從根節點到I深度節點的距離.因為在LCA Tarjan演算法中 ,LCA(設為X) 必然在DFS路徑上,所以X到I的距離為sum[deep[I]]-sum[Deep[X]]
響應時,返回值為:dis[A]+sum[deep[getf(A)]]-sum[Deep[B]];
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>
#define ll long long
using namespace std;
const int inf=0x3ffffff;
const int MAXN = 40010;
const int MAXM = 100008;
const double eps = 1e-6;
struct Edge{
int next, to, info;
}edge[MAXM];
struct Requst {
int next, to;
}request[MAXM];
int head[MAXN], tot;
int n, m;
int first[MAXN], cnt;
int dis[MAXN];
int father[MAXN], level[MAXN], sum[MAXN];
bool vis[MAXN];
int ans[MAXN];
int find(int x) {
if (x == father[x]) {
return x;
}
int ret = find(father[x]);
dis[x] += dis[father[x]];
return father[x] = ret;
}
void dfs(int x, int dep) {
vis[x] = true;
level[x] = dep;
for (int i = first[x]; i != -1; i = request[i].next) {
if (vis[request[i].to]) {
find(request[i].to);
ans[i/2] = dis[request[i].to] + sum[dep] - sum[level[father[request[i].to]]];
//下標是i/2的原因:在存放請求的時候,是存放兩次 其中 i和i|1是一次請求
}
}
for (int i = head[x]; i != -1; i = edge[i].next) {
if (!vis[edge[i].to]) {
sum[dep+1] = sum[dep] + edge[i].info;
dfs(edge[i].to, dep+1);
dis[edge[i].to] = edge[i].info;
father[edge[i].to] = x;
}
}
}
int main() {
#ifndef ONLINE_JUDGE
freopen("1.txt", "r", stdin);
#endif
int i, j, k;
int x, y, w;
char c;
while(~scanf("%d%d", &n, &m)) {
tot = 0;
cnt = 0;
memset(vis, false, sizeof(vis));
memset(head, -1, sizeof(head));
memset(first, -1, sizeof(first));
memset(ans, 0, sizeof(ans));
memset(dis, 0, sizeof(dis));
memset(level, 0, sizeof(level));
for (i = 0; i <= n; i++) {
father[i] = i;
}
for (i = 0; i < m; i++) {
scanf("%d %d %d %c", &x, &y, &w, &c);
edge[tot].to = y;
edge[tot].info = w;
edge[tot].next = head[x];
head[x] = tot++;
edge[tot].to = x;
edge[tot].info = w;
edge[tot].next = head[y];
head[y] = tot++;
}
scanf("%d", &k);
for (i = 0; i < k; i++) {
scanf("%d%d", &x, &y);
request[cnt].to = y;
request[cnt].next = first[x];
first[x] = cnt++;
request[cnt].to = x;
request[cnt].next = first[y];
first[y] = cnt++;
}
sum[0] = 0;
dfs(1, 1);
for (i = 0; i < k; i++) {
printf("%d\n", ans[i]);
}
}
return 0;
}