想了一想幾個月前打的用於解LCA的Tarjan貌似棄坑就沒再管它，然後虛擬機器磁碟被我莫名其妙起爆了以後之前打的程式全都打了水漂就想起了被置之不理的Tarjan解LCA問題的板子，索性就把坑填上唄，畢竟我不是挖坑不填的主 明明還有一堆亂七八糟的平衡樹沒填
LCA就是樹上兩點的最近公共祖先。說這個之前，得先了解一下什麼是樹上兩點的公共祖先。

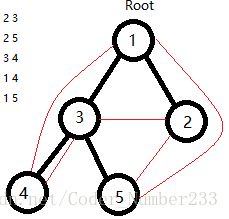
就比如上圖中根節點為t[1]的樹，在其上的節點t[4]和t[5]有兩個公共祖先，一個是它們共有的父親t[3]，一個是它們共有的父親的父親t[1]。如果深度大一點，從它們最開始共有的祖先，即最近公共祖先(LCA)及它們的LCA的所有祖先都是它們的公共祖先。自然，根節點是以它為根的樹上任意兩點的公共祖先。
然而求公共祖先並沒有什麼用。我們所要的只是它們的LCA而已，也就是它們的公共祖先中深度最大的那個節點。線上演算法有ST，不過在這裡我求LCA用的演算法是離線的Tarjan。
Tarjan演算法是建立在一個深度優先搜尋(DFS)上的，它把每一個點對的問題都統計完後通過對整棵樹一遍DFS解決所有問題然後輸出結果。這也是它較暴力演算法時間複雜度大幅降低的原因。
在通過鄰接表的方式(畢竟你也不知道它是幾叉樹)把樹儲存完以後，我們把要求求LCA的所有點對連線起來(自然也是鄰接表儲存噠)做出另一個圖，就像紅色線所標識的那樣:

這樣子我們就有了一個問題集合的無向圖。然後我們就可以從根節點開始遍歷整棵樹，圖上就是從t[1]開始。途中用f[x]的方式記錄當前情況下x所在集合的代表，這個可以用並查集解決。
在DFS到t[x]時我們先初始化f[x]=x，並令vis[x]=true。按照問題的鄰接表查詢一下含有t[x]點的每個問題，如果點對中另一個點t[y]已經走過了(可以開個bool型別的vis陣列解決此問題)，那就把相應標號的問題寫上解為find(y)（就是並查集find()操作啦），否則不予置理。之後我們遍歷一遍與t[x]相連的樹上的所有邊，只要與t[x]相連的點t[z]的vis[z]=false，t[z]就必定是t[x]的兒子之一，我們就可以遞迴再搜尋一遍t[z]，搜尋完後令f[z]=x，直到遍歷完整棵樹。
因為在把整棵樹遍歷的過程中，我們手推一下就能知道以節點t[x]為根的樹中所有節點都遍歷過之前，f[x]一定是x，所以可以得出只要是已經能解決的要求就必定是最近的公共祖先的結論。LCA問題也就解決了。
最後例行上程式碼：

#include<cstdio>
#define maxn 500005
#define maxm 1000001
int f[maxn],t[maxn],nx[maxm],v[maxm],a[maxm<<1];
int T[maxn],Nx[maxm],V[maxm],ans[maxn],h;
int n,m,s;bool vis[maxn];
int find(int x){
    if(f[x]!=x)f[x]=find(f[x]);
    return f[x];
}
void dfs(int r){int k;vis[r]=1;f[r]=r;
    k=t[r];while
 
(k){
        if(vis[v[k]])ans[a[k]]=find(v[k]);
        k=nx[k];
    }k=T[r];while(k){
        if(!vis[V[k]])dfs(V[k]),f[V[k]]=r;
        k=Nx[k];
    }
}
int main(){int i,b,e;
    scanf("%d%d%d",&n,&m,&s);
    for(i=1;i<n;i++){
        scanf("%d%d",&b,&e);
        Nx[++h]=T[b],T[b]=h,V[h]=e;
        Nx[++h]=T[e],T[e]=h,V[h]=b;
    }for(h=0,i=1;i<=m;i++){
        scanf("%d%d",&b,&e);
        nx[++h]=t[b],t[b]=h,v[h]=e,a[h]=i;
        nx[++h]=t[e],t[e]=h,v[h]=b,a[h]=i;
    }dfs(s);
    for(i=1;i<=m;printf("%d\n",ans[i]),i++);
}

The End