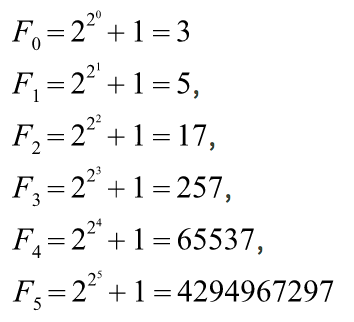0x01 普遍形式

費馬素數也叫費馬質數。

其中 n 為非負整數。

0x02 歷史

法國數學家費馬於1640年提出了以下猜想：

可以看出，前4個是質數，因為第5個數實在太大了，費馬認為是質數。

由此提出（費馬沒給出證明），形如 的數都是質數的猜想。後來人們就把形如 的數叫費馬數。

1732年，尤拉算出第五個費馬數 4294967297 = 641 × 6700417 不是質數，宣佈了費馬的這個猜想不成立，它不能作為一個求質數的公式。

以後，人們又陸續找到了不少反例：

此後人們對更多的費馬數進行了研究。

隨著電子計算機的發展，計算機成為數學家研究費馬數的有力工具。

但即使如此，在所知的費馬數中竟然沒有再新增一個費馬素數。

迄今為止，費馬素數除了被費馬本人所證實的那五個外沒有再發現一個。

實際上，幾千年來，數學家們一直在尋找這樣的一個能求出所有質數的公式，但直到現在，誰也未能找到這樣一個公式，而且誰也未能找到證據，說這樣的公式就一定不存在或者這樣的公式存不存在，這也就成了一個著名的數學難題。

雖然費馬數作為一個關於指數公式的嘗試失敗了，但有意思的是，1801年數學家高斯證明了如果費馬數K為質數，那麼就可以用直尺和圓規將圓周K等分。高斯本人就根據這個定理作出了正十七邊形。