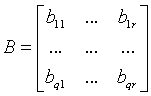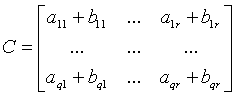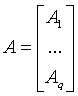矩陣基礎 (3). 分塊矩陣的加法和乘法運算
摘要
本文主要講述分塊矩陣的加法運算和乘法運算。將矩陣進行分塊操作有很多的好處,特別是在高效能平行計算領域內,矩陣的分塊化操作更是有很多益處。
1. 分塊矩陣加法運算
給定矩陣A,B分別如下,
矩陣A+B=C,矩陣C如下,
分塊矩陣的加法運算非常顯然,這裡就不再多費筆墨了。
2. 分塊矩陣的乘法運算
給定矩陣A,B分別如下,(注意:這裡矩陣A,B中的每一個元素都是子矩陣)
矩陣A*B=C,矩陣C如下,
分塊矩陣的乘法運算也比較直觀,但是相比於其加法運算而言,乘法運算顯然會難一點。
3. 分塊矩陣運算小結
分塊矩陣做的是一個非常顯然的事情是對矩陣乘法粒度的變大化。更加細一點而言,一般的矩陣乘法每一次對矩陣中的一個數進行累積和運算。而分塊矩陣面向的操作物件是一個個的子矩陣,顯然兩者在計算的粒度上有很多的不同。至於子矩陣的粒度的大小,取決於一個執行緒能夠用到的記憶體的大小和其計算能力,每一個執行緒能用到的記憶體越大,能用到的計算能力越大相應地,每一個子執行緒的運算處理能力就越大,子矩陣的粒度也就可以大一些。反之,則子矩陣粒度小些。最後,希望我足夠虔誠,也希望讀者能在本文中有所收穫。
相關推薦
矩陣基礎 (3). 分塊矩陣的加法和乘法運算
摘要 本文主要講述分塊矩陣的加法運算和乘法運算。將矩陣進行分塊操作有很多的好處,特別是在高效能平行計算領域內,矩陣的分塊化操作更是有很多益處。 1. 分塊矩陣加法運算 給定矩陣A,B分別如下, 矩陣A+B=C,矩陣C如下, 分塊矩陣的加法運算非常顯然,這裡就不再多費
LOJ #6279. 數列分塊入門 3-分塊(區間加法、查詢區間內小於某個值x的前驅(比其小的最大元素))
posit head -c tar psu typedef small -h scu #6279. 數列分塊入門 3 內存限制:256 MiB時間限制:1500 ms標準輸入輸出 題目類型:傳統評測方式:文本比較 上傳者: hzwer 提
整數的加法和乘法運算
深入理解計算機系統第二章讀書筆記 在程式設計入門的時候可能都知道兩個正數相加的結果可能為負數,還有一個更奇怪的現象就是:x < y和 x - y < 0兩個表示式可能會得出不一樣的結果,這些神奇的結果都和計算機整數的底層表示和運算有著密切
大整數的加法和乘法運算
C和C++中整數最大隻能表示10位,不然就會溢位,所以出現瞭如何避免整數溢位的問題。其中一個方法就是使用字串來表示,使用字串的長度是沒有限制的。 使用字串表示整數然後進行乘法運算的關鍵有如下幾點: 被乘數和乘數相乘時最開始不處理進位,而是每一位相乘的計算結果都是用整數來
POJ 3233 Matrix Power Series(求矩陣冪的和——分塊矩陣快速冪 or 二分遞迴+矩陣快速冪)
Matrix Power Series Time Limit: 3000MS Memory Limit: 131072K Total Submissions: 21451 Accepted:
[R]R語言中用cbind() 和rbind() 構建分塊矩陣
用cbind() 和rbind() 構建分塊矩陣正如前面所暗示的,可以利用函式cbind() 和rbind() 把向量和矩陣拼成一個新的矩陣。概略地說,cbind() 把矩陣橫向合併成一個大矩陣(列方式),而rbind()是縱向合併(行方式)。在命令中> X <
Latex 分塊矩陣的處理
begin code col log 分塊 class lam 如果 gin 在 \(\mathrm{\LaTeX}\) 中,如果想輸入類似的矩陣: 可以這樣實現: \[ \left[ \begin{array}{cc|cc|c} \lambda &
二維數據練習--矩陣的加法和乘法
問題 矩陣的乘法 mage 嘗試 auth out 轉置 args lis 數組的練習示例展示: package arrayList; /** * 矩陣的集中運算法則:求和,求積,求逆矩陣,轉置矩陣...... * @author Drew * */ public
HDU-6395多校7 Sequence(除法分塊+矩陣快速冪)
review lse %d sca code left define hdu fin Sequence Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others
線性代數分塊矩陣的練習
需要計算兩個2*2矩陣的乘法,2*2矩陣求逆的公式需要記熟 這是一個3*3可以分為1*1和2*2塊的例子,求a使用2*(9-a^2)=10-》a=2 根據分塊矩陣,直接寫出一個特徵值2,(1,0,0),另外兩個特徵向量求解2*2的矩陣,(0,x,y),(0,x1,y1
分塊矩陣求行列式
分塊矩陣求行列式 將矩陣寫為 P = [A,B;B,A],那麼det(P)=det(A)det(A-BA^-1B)=def(A-BA^-1B) a=[1;-1] A*a=b1 B*a=b2 a=0或a=1均可構造無窮多解 def(A)*
poj 3233 Matrix Power Series (構造分塊矩陣)
題目連結:哆啦A夢傳送門 題意:自己看。 參考部落格:神犇 題解:分塊矩陣:分塊矩陣可以構造求和。 例如:我們可以這樣構造, 還需注意一點的是:算完S(k+1),取出右上角矩陣分塊後,還需減掉單位矩陣E。 程式碼不是我寫的,我就按自己習慣改了下變數
2018 Multi-University Training Contest 7 1010 Sequence【整數分塊+矩陣冪】
題意:在擴充套件斐波納挈的基礎上加了一個變數P/nP/n。求第nn項的取值。 分析:考慮將每一種P/nP/n進行矩陣快速冪,也就是進行了整數分塊處理。對於每一個整數塊可以使用矩陣快速冪,然後維護A,BA,B用作下一次的矩陣快速冪使用。 整數分塊: 通過
HDU 6395 Sequence 矩陣快速冪+分塊
Let us define a sequence as below Your job is simple, for each task, you should output Fn module 109+7. Input The first line has only
暴力分塊矩陣乘法
題引 題解 樸素的演算法 O(4096 * 64 * 4096) = O(1e9) 不用想是超時的。 因為每次矩陣乘法中存在很多重複的計算。 考慮將矩陣進行分塊優化。預處理出每塊的值。 怎麼分塊。考慮對A矩陣的列分塊,和B矩陣的行分塊。因為p是公共的邊,
【洛谷 P5110】 塊速遞推(矩陣加速,分塊打表)
題目連結 掌握了分塊打表法了。原來以前一直想錯了。。。 塊的大小\(size=\sqrt n\),每隔\(size\)個數打一個表,還要在\(0\text{~}size-1\)每個數打一個表。 然後就可以做到\(O(1)\)查詢了。 比如要求\(A^{n}\),只需要算出\(biao[n/size]*pow
matlab矩陣分塊與把分塊矩陣還原
A=rand(256,64); %將A分塊 B=mat2cell(A,ones(256/16,1)*16,ones(64/16,1)*16); %ones(a,b)為建立a行b列的值為1
matlab 分塊 矩陣 對角 合併
引用:http://www.ilovematlab.cn/thread-74502-1-1.html 如:A=[ 1 2 3 2 3 4] B=[1 2
poj 3233 矩陣乘法(分塊矩陣)
題解:Sn為所求矩陣, 則 這樣, 此題就變成了求矩陣冪和矩陣乘法, 分塊矩陣乘法和普通矩陣一樣的。 code: /* adrui's submission Language : C++ Result : Accepted Love : ll Favorite
hdu 6395 Sequence 分塊矩陣快速冪
容易知道 p/i (i=3......n); 在某一區間內是相同的,記錄前一個區間的fn-1,fn-2,對本區間進行矩陣快速冪,確定本區間的界限可以用一句話 即 j=(p/i)==0?n:min(n,p/(p/i)),並不需要二分; AC 程式碼 #include