線性代數分塊矩陣的練習

阿新 • • 發佈：2018-11-16

ååç©éµçéç©éµçå¬å¼è®°å¿æ¹æ³

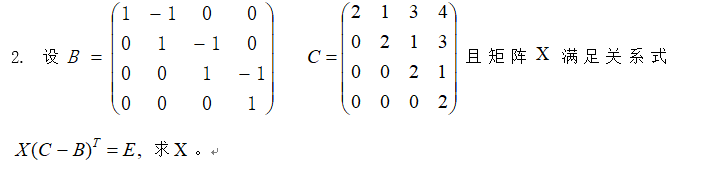
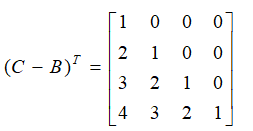
需要計算兩個2*2矩陣的乘法,2*2矩陣求逆的公式需要記熟

這是一個3*3可以分為1*1和2*2塊的例子，求a使用2*(9-a^2)=10-》a=2

根據分塊矩陣，直接寫出一個特徵值2，（1，0，0），另外兩個特徵向量求解2*2的矩陣，（0，x，y），（0，x1,y1)

如果在熟悉的話，可以直接寫出後面空間的特徵向量是一個對稱，一個反對稱。立刻可以得到

需要計算兩個2*2矩陣的乘法,2*2矩陣求逆的公式需要記熟這是一個3*3可以分為1*1和2*2塊的例子，求a使用2*(9-a^2)=10-》a=2 根據分塊矩陣，直接寫出一個特徵值2，（1，0，0），另外兩個特徵向量求解2*2的矩陣，（0，x，y），（0，x1,y1

begin code col log 分塊 class lam 如果 gin 在 \(\mathrm{\LaTeX}\) 中，如果想輸入類似的矩陣：可以這樣實現： \[ \left[ \begin{array}{cc|cc|c} \lambda &

review lse %d sca code left define hdu fin Sequence Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others

blog 線性方程組能夠向量 alt 過程 http ont 形式　　在線性代數中， LU分解(LU Decomposition)是矩陣分解的一種，可以將一個矩陣分解為一個單位下三角矩陣和一個上三角矩陣的乘積（有時是它們和一個置換矩陣的乘積）。LU分解主要應用在數值分

1.消元法 method of elimination 高斯消元法：就是對矩陣進行行或列的加減，變換成對角陣的形式。 2.回代 Back substitution 做方程的高斯消元法時可以將係數矩陣加上b擴充為增廣矩陣，再進行高斯消元 3.消元矩陣左

分塊矩陣求行列式將矩陣寫為 P = [A,B;B,A],那麼det(P)=det(A)det(A-BA^-1B)=def(A-BA^-1B) a=[1;-1] A*a=b1 B*a=b2 a=0或a=1均可構造無窮多解 def(A)*

練習-1 4.區間加法與求和給出一個長為的數列，以及個操作，操作涉及區間加法，區間求和。資料範圍: 相對與第一題的單點查詢,需要多維護一個區間的區間和屬性記錄整塊加的值,維護初始以及非整塊操作時的塊的和 #include <cstdio>

上一個部落格（機器學習--高等數學篇--線性代數篇01--行列式）已經講解過行列式的概念，本將將講解下矩陣的概念和矩陣的一些運算規則。一、矩陣的定義： m行n列個數，加上圓括號或者方括號，組成的就是m✖n的矩陣，記作Amxn。方陣：矩陣的行和列數相等。單位矩

上一節講解了矩陣的一些基礎概念和運演算法則（機器學習--高等數學篇--線性代數篇02--矩陣01），本章將學習並瞭解伴隨矩陣和逆矩陣。一、伴隨矩陣 1.定1義：A是n階方陣，可以得到一個行列式|A|，求出|A|的代數餘子式，共有n^2個數。把代數餘子式按照第一行寫成第一

題目連結：哆啦A夢傳送門題意：自己看。參考部落格：神犇題解：分塊矩陣：分塊矩陣可以構造求和。例如：我們可以這樣構造，還需注意一點的是：算完S(k+1)，取出右上角矩陣分塊後，還需減掉單位矩陣E。程式碼不是我寫的，我就按自己習慣改了下變數

當 A A A 是對稱的時候，

目錄基礎概念矩陣轉置對角矩陣線性相關範數正交特徵值分解奇異值分解跡運算行列式如果這篇文章對你有一點小小的幫助，請給個關注喔~我會非常開心的~ 基礎概念標量：一個標量就是一個單獨的數字向量：一個向量就是一列數字矩

題意：在擴充套件斐波納挈的基礎上加了一個變數P/nP/n。求第nn項的取值。分析：考慮將每一種P/nP/n進行矩陣快速冪，也就是進行了整數分塊處理。對於每一個整數塊可以使用矩陣快速冪，然後維護A，BA，B用作下一次的矩陣快速冪使用。整數分塊：通過

說明：以後前一部分主要講各種定義以及定理，用題目對定理來進行說明則放到後一板塊定義：中的一個子空間是中的集合H，具有以下三個性質： a. 零向量屬於H b. 對H 中的任何向量u和v，u+v屬

題引題解樸素的演算法 O(4096 * 64 * 4096) = O(1e9) 不用想是超時的。因為每次矩陣乘法中存在很多重複的計算。考慮將矩陣進行分塊優化。預處理出每塊的值。怎麼分塊。考慮對A矩陣的列分塊，和B矩陣的行分塊。因為p是公共的邊,

前面大概有2年時間，利用業餘時間斷斷續續寫了一個機器學習方法系列，和深度學習方法系列，還有一個三十分鐘理解系列（一些趣味知識）；新的一年開始了，今年給自己定的學習目標——以補齊基礎理論為重點，研究一些基礎課題；同時逐步繼續寫上述三個系列的文章。最近越來越多的

摘要本文主要講述分塊矩陣的加法運算和乘法運算。將矩陣進行分塊操作有很多的好處，特別是在高效能平行計算領域內，矩陣的分塊化操作更是有很多益處。 1. 分塊矩陣加法運算給定矩陣A，B分別如下，矩陣A+B=C，矩陣C如下，分塊矩陣的加法運算非常顯然，這裡就不再多費

A=rand(256,64); %將A分塊 B=mat2cell(A,ones(256/16,1)*16,ones(64/16,1)*16); %ones（a,b）為建立a行b列的值為1

參考了《深度學習》鉅作，以下是矩陣篇的目錄。 1 矩陣的乘法設矩陣A為m×n矩陣，B為n×p矩陣，則它們的乘法公式為：相關程式碼實現： # 矩陣滴乘法運算 # 注意：需要傳入np.matrix型別資料 def Matrix_Mul(a,b):

原地址：https://blog.csdn.net/mathmetics/article/details/9269451將矩陣抽象為線性變換來考慮是很有必要的，這樣會有很多好處：簡化符號，簡化證明，便於理解逆矩陣等概念，對於將來研究無限維空間也是很有必要的。1 對映對映這個概