目錄

1. 問題背景

NFL(No Free Lunch Theorem)告訴我們選擇演算法應當與具體問題相匹配，通常我們看一個演算法的好壞就是看其泛化效能，但是對於一個演算法為什麼好為什麼壞，我們缺乏一些認識。“Bias-Variance Decomposition”就是從偏差和方差的角度來解釋一個演算法的泛化效能。

2. 一點點數學

“Bias-Variance Decomposition” 是以測試集上的平方錯誤為基礎的，假設我們的預測值為g(x)$g(x)$,真實值為f(x)$f(x)$,則均方誤差為E((g(x)−f(x))2)$E((g(x)-f(x){)}^2)$。

為了讓世界更加美好，我們在這裡不考慮樣本的噪聲。

“The noise term is unaviodable no matter what we do, so the terms we are interested in are really the bias and variance”(from “Learning From Data” Page 64)

（噪聲的存在是學習演算法所無法解決的問題，資料的質量決定了學習的上限。而假設在資料已經給定的情況下，此時上限已定，我們要做的就是儘可能的接近這個上限）

並且使用g$g$來代表預測值（這裡我們把它看成是隨機變數，即不同資料學習得到的模型）, f$f$代表真實值, g¯=

E(g)$\overline{g}=E(g)$代表演算法的期望預測（如：可以用不同的資料集D1,D2,...,DK$D_1,D_2,...,D_K$來得到g¯=1K∑kgk(x)$\overline{g}=\frac{1}{K}\sum _k{g}_k(x)$），則有：

E(g−f)2=E(g2−2gf+f2)=E(g2)−g¯2+(g¯−f)2=E(g2)−2g¯2+g¯2+(g¯−f)2=E(g2−2gg¯2+g¯2)+(g¯−f)2=E(g−g¯)2var(x)+(g¯−f)2⏟bias2(x)(1)(2)(3)(4)(5)$$\begin{array}{}\text{(1)}& E(g-f{)}^2& =E(g^2-2gf+f^2)\text{(2)}& =E(g^2)-{\overline{g}}^2+(\overline{g}-f{)}^2\text{(3)}& =E(g^2)-2{\overline{g}}^2+{\overline{g}}^2+(\overline{g}-f{)}^2\end{array}$$

(4)=E(g2−2gg¯2+g¯2)+(g¯−f)2(5)=E(g−g¯)2⏟var(x)+(g¯−f)2⏟bias2(x)

3. 偏差與方差

由上面的公式可知，偏差描述的是演算法的預測的平均值和真實值的關係（可以想象成演算法的擬合能力如何），而方差描述的是同一個演算法在不同資料集上的預測值和所有資料集上的平均預測值之間的關係（可以想象成演算法的穩定性如何）。
（ps：個人認為可以把偏差認為是單個模型的學習能力，而方差則描述的是同一個學習演算法在不同資料集的不穩定性）
偏差和方差的形象展示如下圖所示（圖片引自Understanding the Bias-Variance Tradeoff ）

圖中的紅色位置就是真實值所在位置，藍色的點是演算法每次預測的值。
可以看出，偏差越高則離紅色部分越遠，而方差越大則演算法每次的預測之間的波動會比較大。

4. 偏差方差窘境

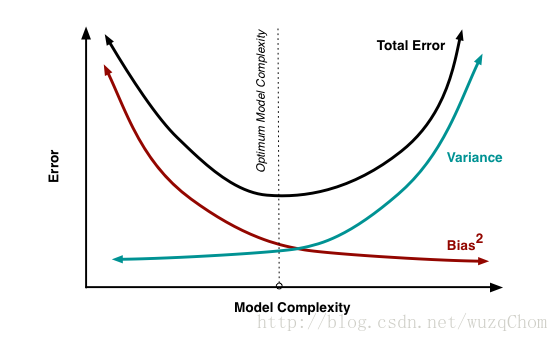
從圖中我們可以看出，偏差和方差兩者是有衝突的，稱之為變差方差窘境（bias-variance dilemma）。

假如學習演算法訓練不足時，此時學習器的擬合能力不夠強，此時資料的擾動不會對結果產生很大的影響（可以想象成由於訓練的程度不夠，此時學習器指學習到了一些所有的資料都有的一些特徵），這個時候偏差主導了演算法的泛化能力。隨著訓練的進行，學習器的擬合能力逐漸增強，變差逐漸減小，但此時不同通過資料學習得到的學習器就可能會有較大的偏差，即此時的方差會主導模型的泛化能力。若學習進一步進行，學習器就可能學到資料集所獨有的特徵，而這些特徵對於其它的資料是不適用的，這個時候就是發生了過擬合的想象。

5. Bagging和Boosting

Bagging和Boosting是整合學習當中比較常用的兩種方法，剛好分別對應了降低模型方差和偏差。

Bagging是通過重取樣的方法來得到不同的模型，假設模型獨立則有：
E(∑iE(Xi)n)

相關推薦

正則化——“偏差（bias）”與“方差（variance）”

正則化後的線性迴歸模型 模型 \[{h_\theta }\left( x \right) = {\theta _0} + {\theta _1}x + {\theta _2}{x^2} + {\theta _3}{x^3} + {\theta _4}{x^4}\] \[J\left( \theta&nb

偏差（Bias）與方差（Variance）

目錄 1. 問題背景 NFL(No Free Lunch Theorem)告訴我們選擇演算法應當與具體問題相匹配，通常我們看一個演算法的好壞就是看其泛化效能，但是對於一個演

偏差（bias）和方差（variance）——KNN的K值、RF樹的數量對bias和variance的影響

機器 image str 領域 什麽 認識 綜合 10個 機器學習算法 1.前言：為什麽我們要關心模型的bias和variance？ 　　大家平常在使用機器學習算法訓練模型時，都會劃分出測試集，用來測試模型的準確率，以此評估訓練出模型的好壞。但是，僅在一份測試集上測試，存在

數學期望與方差E(X) D（X）

數學期望 ：  1.設X是隨機變數，A,B是常數，則E（AX+B）=CE（X）+B 2.設X，Y是任意兩個隨機變數，則有E（X+Y）=E（X）+E（Y）.3.設X,Y是相互獨立的隨機變數，則有E（XY）=E（X）E（Y） 方差：  1、設A是常數，則D（A）=0  2、設

均方誤差、平方差、方差、均方差、協方差（轉）

相差 均方差 nbsp 無法 bsp 技術 方法 簡便 但是 一，均方誤差 作為機器學習中常常用於損失函數的方法，均方誤差頻繁的出現在機器學習的各種算法中，但是由於是舶來品，又和其他的幾個概念特別像，所以常常在跟他人描述的時候說成其他方法的名字。 均方誤差的數學表達為：

【題解】[牛客網NOIP賽前集訓營-提高組（第二場）]A.方差 字首和

題目連結 我們把方差公式進行化簡。記 s u m

從多個角度來理解協方差（covariance）

起源：協方差自然是由方差衍生而來的，方差反應的是一個變數（一維）的離散程度，到二維了，我們可以對每個維度求其離散程度，但我們還想知道更多。我們想知道兩個維度（變數）之間的關係，直觀的舉例就是身高和體重（青少年），我們採集到的資料裡面有一種固有的性質，那就是身高越高的樣本似乎總有著更大的體重，那我們如何衡量這種

角度的均值與標準差（circular data/ directional statistics）

參考： 1. Directional statistics（Mardia）P14-19&29-30&47-50; 2. Biostatistical Analysis（2009 Zar）-5th edition P614-617; 3. CircStat: A

協方差（Covariance）

統計學上用方差和標準差來度量資料的離散程度 ，但是方差和標準差是用來描述一維資料的（或者說是多維資料的一個維度），現實生活中我們常常會碰到多維資料，因此人們發明了協方差（covariance），用來度量兩個隨機變數之間的關係。   我們仿照方差的公式來定義協方差： 方差：  協方差

為什麼樣本方差（sample variance）的分母是 n-1？

樣本方差計算公式裡分母為的目的是為了讓方差的估計是無偏的。無偏的估計(unbiased estimator)比有偏估計(biased estimator)更好是符合直覺的，儘管有的統計學家認為讓mean square error即MSE最小才更有意義，這個問題我們不在這裡

方差（Variance）和標準差（Standard Deviation）

轉自：http://book.51cto.com/art/201004/193276.htm 方差是總體所有變數值與其算術平均數偏差平方的平均值，它表示了一組資料分佈的離散程度的平均值。標準差是方差的平方根，它表示了一組資料關於平均數的平均離散程度。   其中， 為總

為什麼樣本方差（sample variance）的分母是 n-1

要回答這個問題，偷懶的辦法是讓困惑的題主去看下面這個等式的數學證明：. 但是這個答案顯然不夠直觀（教材裡面統計學家像變魔法似的不知怎麼就得到了上面這個等式）。 下面我將提供一個略微更友善一點的解釋。 =======================================================

Java學習筆記——排序算法之進階排序（堆排序與分治並歸排序）

進行 技術分享 ring http 沒有 oid 有序 重復 調整 春蠶到死絲方盡，蠟炬成灰淚始幹 　　　　　　　　　　　　　　——無題 這裏介紹兩個比較難的算法： 1、堆排序 2、分治並歸排序 先說堆。 這裏請大家先自行了解完全二叉樹的數據結構。 堆是完全二叉樹。

JS入門基礎（if else 與 switch case / node安裝）

json health 案例 js文件 動作 require 步驟 *** 命令 在 JavaScript 中，為不同的決定來執行不同的動作，我們可使用以下條件語句： if 語句 - 只有當指定條件為 true 時，使用該語句來執行代碼 if...else 語句 - 當條

位運算（&、|、^）與邏輯運算（&&、 ||）差別

邏輯與 清空 作用 一個數 總結 與運算 位或 定位 按位與 剛無意在一篇文章中看到了位運算（&、|）和邏輯運算（&&、||）的介紹。想起了自己薄弱的基礎知識。於是百度了幾把總結了下。 首先從概念上區分下，位

走入計算機的第二十七天（模塊與包的調用）

項目 conf form 第一時間 生產環境 兩個 nag 不同 spec 一 模塊（module）的概念 在計算機程序的開發過程中，隨著程序代碼越寫越多，在一個文件裏代碼就會越來越長，越來越不容易維護。 為了編寫可維護的代碼，我們把很多函數分組，分別放到不同的文件裏，每個

C# Socket簡單例子（服務器與客戶端通信）

項目 回車 pop ace log () client protocol comm 這個例子只是簡單實現了如何使用 Socket 類實現面向連接的通信。 註意：此例子的目的只是為了說明用套接字寫程序的大概思路，而不是實際項目中的使用程序。在這個例子中，實際上還有很多問題

css基礎語法一（選擇器與css導入方式）

數字 mic link html clas ref height font 兼容 頁面中，所有的CSS代碼，需要寫入到<style></style>標簽中。style標簽的type屬性應該選擇text/css，但是type屬性可以省略。 CS

echarts中視覺映射器（visualMap）與時間軸（timeline）混用的實現方法

images mon label axis poi max 時間軸 asc clas 1、簡述　　echarts中的 timeline 組件，提供了在多個 ECharts option 間進行切換、播放等操作的功能。　　與其他組件些不同，它需要操作『多個option』。 所

【轉】文件下載之斷點續傳（客戶端與服務端的實現）

http協議 當前時間 end box [] ada demo 服務端 sem 【轉】文件下載之斷點續傳（客戶端與服務端的實現） 【轉】文件下載之斷點續傳（客戶端與服務端的實現） 前面講了文件的上傳，今天來聊聊文件的下載。 老規矩，還是從最簡單粗暴的開始。那麽多簡單算簡單