圖論演算法將地圖結點和結點之間的通路資訊用有向或者無向鄰接矩陣來進行儲存，鄰接矩陣中相連的兩點對應值為1，不相連的對應值為0，同一個圖中可以有多種深度優先序列和廣度優先序列。在路徑搜尋中可以將相鄰兩點的對應值設定為兩者的距離權重值，在演算法搜尋結束後選擇距離最短的路徑分支，從而確定一條演算法上最優的路徑序列。

        深度優先搜尋(DFS, Depth First Search)和廣度優先搜尋(BFS, Breadth First Search)都是按照一定規則進行的盲目搜尋。

深度優先：

        深度優先搜尋的邏輯規則為從起點開始，尋找訪問下一個連通的結點，直到沒有未訪問的連通結點後，回溯到起點並從其他的分支繼續尋找深度連通路徑，直到所有的結點都被訪問到為止。

假設圖3-9中無向圖的起點為V1，則有以下幾種深度優先序列：

V1, V3, V5, V4, V2;

V1, V4, V5, V3;

V1, V4, V2;

V1, V2, V4, V5, V3;

根據確定的目的結點以及連線的權值和可從序列中擷取選擇最短路徑；

廣度優先：

        廣度優先搜尋的搜尋邏輯為從起點開始，遍歷所有相連的結點並設定為起點的子結點，之後在子節點進行同樣的遞迴操作，直到所有結點都加入以起點為根結點的樹中。

假設圖3-10中有向圖的起點依舊為V1，其中一個廣度優先搜尋序列為：

V1, V3, V4, V2, V5

如圖3-11中所示的兩棵廣度優先搜尋樹，從第二層開始，樹的一層代表一次廣度優先搜尋。

雙向廣度優先：

雙向廣度優先演算法是為了加快收斂速度，從起點和終點同時進行廣度優先搜尋設計的演算法。

3.6 Dijkstra單源最短路徑搜尋演算法

        Dijkstra演算法是A start演算法的無啟發函式版,同時是一種典型的貪心演算法。演算法沒有利用結點本身與起點和目的點的距離資訊進行引導，在整個地圖的所有結點中進行搜尋，體現其盲目性，效率自然比A*演算法低。演算法的本質搜尋思想是對於A和B兩個結點，如果從整個地圖中新增某些中間結點可以使A和B之間的加權路徑長度更短，則加入中間結點構成A和B之間更短的加權路徑，直到沒有中間結點可以使A、B兩點之間路徑更短為止。

        演算法初始化時計算各結點到其他結點的直接距離表，結點之間相連的距離為結點連線的權重值，不相連的距離設定為無窮大。構建一個S表，表示計算完成的結點的集合，演算法開始時將起點加入S表，然後搜尋與起點距離最近的點加入S表，並以新加入的結點為中間結點，計算起點到其他結點的相對更近距離，更新起點的距離表，直到所有的結點都加入S表。起點最終的距離表中的距離值即起點到其他各結點之間的最短路徑距離。當終點確定時，記錄在演算法執行過程中起始點之間加入了那些中間結點，即可找出相應的最短路線。

假設圖3-10有向圖中的起點為V1，則Dijkstra演算法初始化的距離表如表3-1所示：

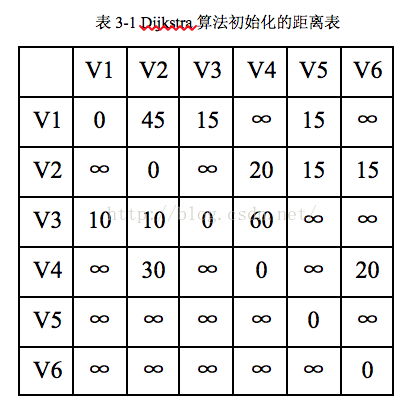
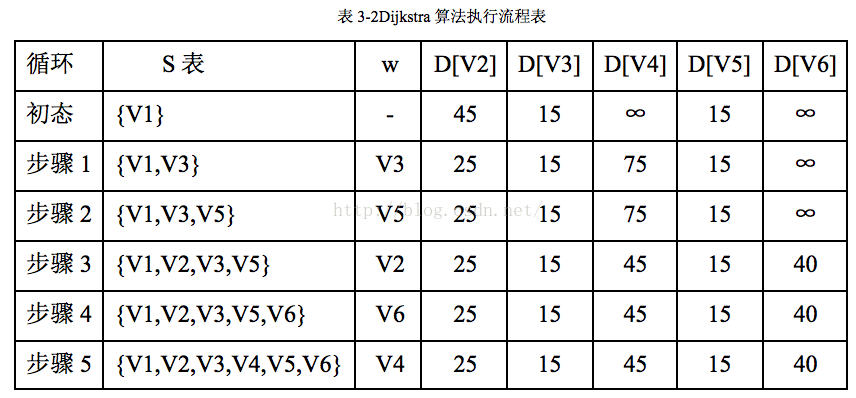
        演算法的執行過程可用表3-2表示如下，共六個結點執行五次迴圈將所有結點加入S表，w為新加入結點，D[Vi]表示起點到結點Vi的最短距離。

3.7隨機尋路演算法

        遊戲中的怪物在玩家還未靠近時要有自己自然的隨機動作，以一個隨機的方向和隨機的速率進行移動，使其看上去是活躍的。當玩家靠近進入怪物的“境界區域”時，怪物會主動尋路靠近玩家，當玩家與怪物足夠近進入怪物的“攻擊區域”時，怪物開始攻擊玩家。

隨機尋路演算法的實現是設計一種隨機移動規則，使遊戲角色不斷產生不規則、不可預見的行動，從而使角色在遊戲中自行保持活躍狀態，提高遊戲真實感。尋路的隨機主要是角色行進的方向和行進速度的隨機。方向的表示可用一個隨機目的地位置表示，或用一個單位方向向量表示。速度的改變可以通過控制更新的頻率或者每次移動的距離實現。

        比如可以用一個向量的方向表示當前行進的方向，的模的大小來表示行進的速度，按照一定週期隨機更新的方向和模的大小實現隨機移動，同時使用碰撞避免演算法來校正尋路，防止遊戲角色出現在障礙物處長時間卡頓徘徊的現象。