以下都是來自網際網路中的摘抄與總結，難免有不對或理解錯誤之處，也希望各位不吝嗇指出，賜教！
可參考此文章幫助理解：　圖解SSL/TLS協議（阮一峰）

1. DEA (Data Encryption Algorithm，即 資料加密演算法）

常用加密演算法為：AES 、 RSA/ECC 、Diffie-hellman 、 SHA-1/SHA-256(資料驗證與指紋) 。

2. 對稱加密演算法

1. DES (DES全稱為Data Encryption Standard，即資料加密標準)

是一種使用金鑰加密的塊演算法，1976年被美國聯邦政府的國家標準局確定為聯邦資料處理標準（FIPS），隨後在國際上廣泛流傳開來。

單金鑰演算法,是資訊的傳送方採用金鑰A進行資料加密,資訊的接收方採用同一個金鑰A進行資料解密.

缺點:由於採用同一個金鑰進行加密解密,在多使用者的情況下,金鑰保管的安全性是一個問題.

2. AES （Advanced Encryption Standard，即 高階加密標準），又稱Rijndael加密法

嚴格地說，AES和Rijndael加密法並不完全一樣（雖然在實際應用中二者可以互換），因為Rijndael加密法可以支援更大範圍的區塊和金鑰長度：AES的區塊長度固定為128 位元，金鑰長度則可以是128，192或256位元；而Rijndael使用的金鑰和區塊長度可以是32位的整數倍，以128位為下限，256位元為上限。加密過程中使用的金鑰是由Rijndael金鑰生成方案產生。

AES是美國國家標準技術研究所NIST旨在取代DES的21世紀的加密標準。

AES_128_GCM 更安全
AES_128_CBC
…

3. 非對稱加密演算法

1. RSA 非對稱加密

1. RSA公鑰加密演算法是1977年由羅納德·李維斯特（Ron Rivest）、阿迪·薩莫爾（Adi Shamir）和倫納德·阿德曼（Leonard Adleman）一起提出的。1987年首次公佈，當時他們三人都在麻省理工學院工作。RSA就是他們三人姓氏開頭字母拼在一起組成的。
2. RSA是目前最有影響力的公鑰加密演算法，它能夠抵抗到目前為止已知的絕大多數密碼攻擊，已被ISO推薦為公鑰資料加密標準。
3. RSA的安全性是基於極其困難的大整數的分解（兩個素數的乘積）

2. DSA

1. 基於整數有限域離散對數難題
2. 一般用於數字簽名和認證
3. 在DSA數字簽名和認證中，傳送者使用自己的私鑰對檔案或訊息進行簽名，接受者收到訊息後使用傳送者的公鑰
   來驗證簽名的真實性。
4. DSA只是一種演算法，和RSA不同之處在於它不能用作加密和解密，也不能進行金鑰交換，
   只用於簽名,它比RSA要快很多.

3. ECC

1. RSA 與 DSA 各有優缺點，那有沒一個更好的選擇呢？答案是肯定的，ECC（Elliptic Curves Cryptography）
2. 基於橢圓曲線演算法。
3. ECC 與 RSA 相比，有以下的優點：
   
   1. 相同金鑰長度下，安全效能更高，如160位ECC已經與1024位RSA、DSA有相同的安全強度。
   2. 計算量小，處理速度快，在私鑰的處理速度上（解密和簽名），ECC遠 比RSA、DSA快得多。
   3. 儲存空間佔用小 ECC的金鑰尺寸和系統引數與RSA、DSA相比要小得多， 所以佔用的儲存空間小得多。
   4. 頻寬要求低使得ECC具有廣泛得應用前景。
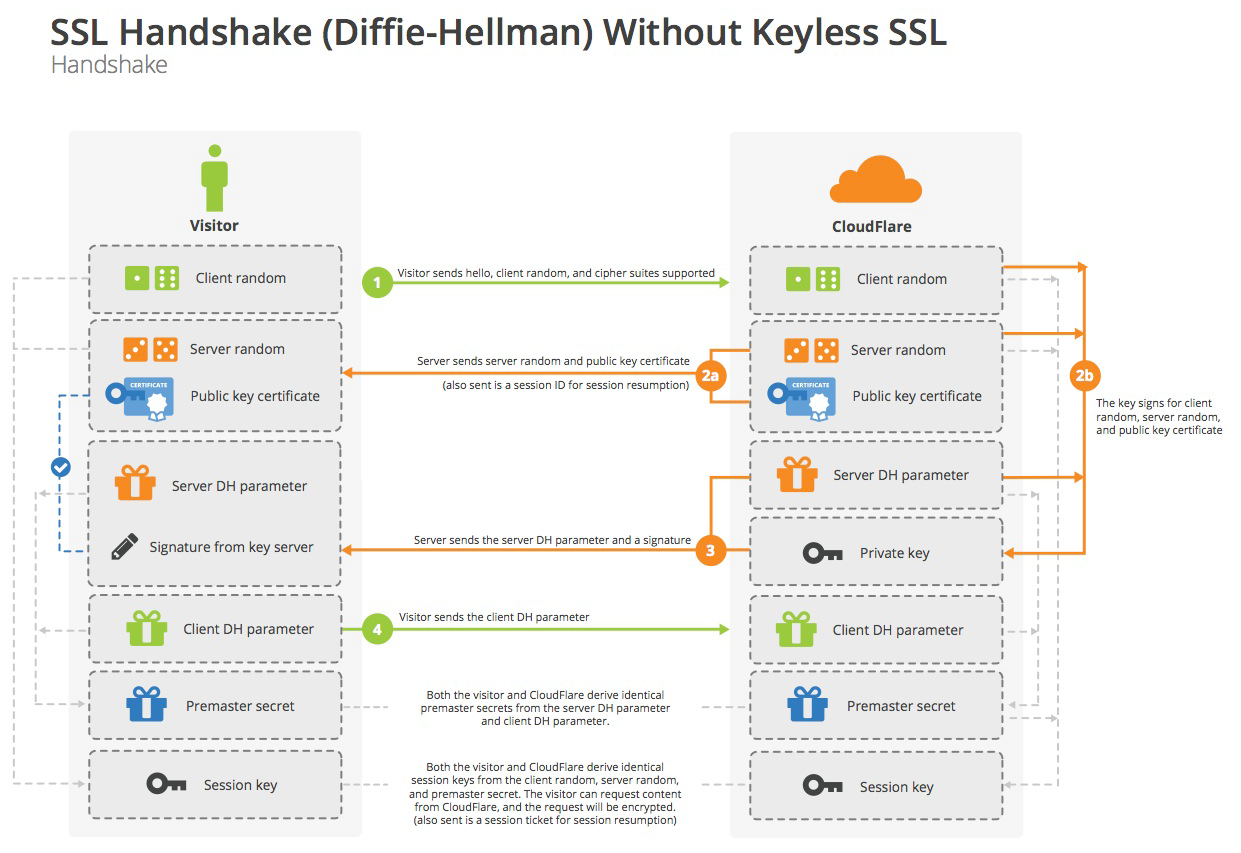
   5. 這使得ECC 取代RSA成為可能。(不知道誰說的)

4. Diffie-Hellman

1. Diffie-Hellman:一種確保共享KEY安全穿越不安全網路的方法，它是OAKLEY的一個組成部分。Whitefield與Martin Hellman在1976年提出了一個奇妙的金鑰交換協議，稱為Diffie-Hellman金鑰交換協議/演算法(Diffie-Hellman Key Exchange/Agreement Algorithm).這個機制的巧妙在於需要安全通訊的雙方可以用這個方法確定對稱金鑰。然後可以用這個金鑰進行加密和解密。但是注意，這個金鑰交換協議/演算法只能用於金鑰的交換，而不能進行訊息的加密和解密。雙方確定要用的金鑰後，要使用其他對稱金鑰操作加密演算法實際加密和解密訊息。
2. DH 演算法的握手階段
   整個握手階段都不加密（也沒法加密），都是明文的。因此，如果有人竊聽通訊，他可以知道雙方選擇的加密方法，以及三個隨機數中的兩個。整個通話的安全，只取決於第三個隨機數（Premaster secret）能不能被破解。
   雖然理論上，只要伺服器的公鑰足夠長（比如2048位），那麼Premaster secret可以保證不被破解。但是為了足夠安全，我們可以考慮把握手階段的演算法從預設的RSA演算法，改為 Diffie-Hellman演算法（簡稱DH演算法）。
   採用DH演算法後，Premaster secret不需要傳遞，雙方只要交換各自的引數，就可以算出這個隨機數。
3. DH演算法的一個簡單描述：
   1) A隨機產生一個大整數a，然後計算Ka=ga mod n。（a需要保密）
   2) B隨機產生一個大整數b，然後計算Kb=gb mod n。（b需要保密）
   3) A把Ka傳送給B,B把Kb傳送給A
   4) A計算K=Kba mod n
   5) B計算K=Kab mod n
   由於Kba mod n= （gb mod n）a mod n= （ga mod n）b mod n，因此可以保證雙方得到的K是相同的，K即是共享的金鑰。
   意思是說client與server端都有一個隨機數是不會通過網路傳輸的。所以保證了安全。
   

4. 資料完整性驗證 (MD5 | SHA-*)

1. MessageDigest是一個數據的數字指紋.即對一個任意長度的資料進行計算,產生一個唯一指紋號.
2. MessageDigest的特性:
   
   1. 兩個不同的資料,難以生成相同的指紋號
   2. 對於指定的指紋號,難以逆向計算出原始資料

5. 例項

1. 使用OPENSSL 生成基於RSA 的非對稱加密演算法 的命令如下：

1. 生成一個金鑰(私鑰)
   [root@hunterfu ~]# openssl genrsa -out private.key 1024
   注意: 需要注意的是這個檔案包含了公鑰和金鑰兩部分，也就是說這個檔案即可用來加密也可以用來解密,後面的1024是生成
   金鑰的長度.
2. 通過金鑰檔案private.key 提取公鑰
   [root@hunterfu ~]# openssl rsa -in private.key -pubout -out pub.key
3. 使用公鑰加密資訊
   [root@hunterfu ~]# echo -n “123456” | openssl rsautl -encrypt -inkey pub.key -pubin >encode.result
4. 使用私鑰解密資訊
   [root@hunterfu ~]#cat encode.result | openssl rsautl -decrypt -inkey private.key
   123456

2. 使用OPENSSL 生成基於DSA 的非對稱加密演算法 的命令如下：

1. 生成一個金鑰(私鑰)
   [root@hunterfu ~]# openssl dsaparam -out dsaparam.pem 1024
   [root@hunterfu ~]# openssl gendsa -out privkey.pem dsaparam.pem
2. 生成公鑰
   [root@hunterfu ~]# openssl dsa -in privkey.pem -out pubkey.pem -pubout
   [root@hunterfu ~]# rm -fr dsaparam.pem
3. 使用私鑰簽名
   [root@hunterfu ~]# echo -n “123456” | openssl dgst -dss1 -sign privkey.pem > sign.result
4. 使用公鑰驗證
   [root@hunterfu ~]# echo -n “123456” | openssl dgst -dss1 -verify pubkey.pem -signature sign.result