import java.util.Scanner;

/**
 * 鄰接矩陣儲存的圖
 * @author liangxiamoyi
 *
 */
public class Graph_Matrix {
	/**
	 * 圖中最大頂點個數
	 */
	public static int MAXGRAPHSIZE=256;
	/**
	 * 圖中最大權值
	 */
	public static int MAXWEIGHT=1000;
	/**
	 * 鄰接矩陣
	 */
	private int[][] edge;
	/**
	 * 當前圖中頂點個數
	 */
	private int graphSize;
	/**
	 * 構造方法
	 */
	public Graph_Matrix(){
		this.edge=new int[MAXGRAPHSIZE][MAXGRAPHSIZE];
		System.out.println("請輸入頂點個數：");
		Scanner sc=new Scanner(System.in);
		this.graphSize=sc.nextInt();
		System.out.println("請依次輸入每條邊的權值：（無窮大為1000，無窮小為0）");
		for(int i=0;i<this.graphSize;i++){
			for(int j=0;j<this.graphSize;j++){
				this.edge[i][j]=sc.nextInt();
			}
		}
	}
	/**
	 * 取得序號為v的頂點的第一個鄰接頂點的序號
	 * @param v 序號v
	 * @return 第一個鄰接頂點的序號
	 */
	public int getFirstNeighbor(int v){
		if(v==-1)return -1;
		for(int i=0;i<this.graphSize;i++){
			if(this.edge[v][i]>0&&this.edge[v][i]<MAXWEIGHT){
				return i;
			}
		}
		return -1;
	}
	/**
	 * 取得v1頂點相對於v2頂點的下一個鄰接頂點
	 * @param v1 頂點v1
	 * @param v2 頂點v2
	 * @return 下一個鄰接頂點的序號
	 */
	public int getNextNeighbor(int v1,int v2){
		if(v1==-1||v2==-1){
			return -1;
		}
		for(int i=v2+1;i<this.graphSize;i++){
			if(this.edge[v1][i]>0&&this.edge[v1][i]<MAXWEIGHT){
				return i;
			}
		}
		return -1;
	}
	/**
	 * 插入一個頂點
	 */
	public void insertVertex(){
		for(int i=0;i<this.graphSize;i++){
			this.edge[i][graphSize]=MAXWEIGHT;
		}
		for(int i=0;i<this.graphSize;i++){
			this.edge[graphSize][i]=MAXWEIGHT;
		}
		this.edge[graphSize][graphSize]=0;
		this.graphSize++;
		System.out.println("插入成功！");
		return ;
	}
	/**
	 * 刪除 一個頂點
	 * @param v 刪除的頂點
	 */
	public void deleteVertex(int v){
		if(v>=this.graphSize){
			System.out.println("無此頂點");
			return;
		}
		for(int i=0;i<this.graphSize;i++){
			this.edge[v][i]=0;
			this.edge[i][v]=0;
		}
		if(v==this.graphSize-1){
			this.graphSize--;
			return;
		}
		for(int i=v+1;i<this.graphSize;i++){
			for(int j=0;j<this.graphSize;j++){
				this.edge[i-1][j]=this.edge[i][j];
			}
		}
		this.graphSize--;
	}
	/**
	 * 插入一條邊
	 * @param v1 起點
	 * @param v2 終點
	 * @param weight 權值
	 */
	public void insertEdge(int v1,int v2,int weight){
		if(v1==v2||v1>this.graphSize||v2>this.graphSize||this.edge[v1][v2]!=MAXWEIGHT){
			System.out.println("插入失敗！");
			return;
		}
		this.edge[v1][v2]=weight;
		System.out.println("插入成功！");
		return;
	}
	/**
	 * 刪除一條邊
	 * @param v1 起點
	 * @param v2 終點
	 */
	public void deleteEdge(int v1,int v2){
		if(v1==v2||v1>this.graphSize||v2>this.graphSize||this.edge[v1][v2]==MAXWEIGHT){
			System.out.println("刪除失敗！");
			return;
		}
		this.edge[v1][v2]=MAXWEIGHT;
		System.out.println("刪除成功");
		return;
	}
	/**
	 * 求圖中任意兩點的最短路徑
	 */
	public void allLengths(){
		int n=this.graphSize;
		int[][] path=new int[n][n];//相應路徑上頂點j的前一個頂點
		int[][] a=new int[n][n];//兩點最短路徑長度
		for(int i=0;i<n;i++){
			for(int j=0;j<n;j++){
				a[i][j]=edge[i][j];
				if(i!=j&&a[i][j]<MAXGRAPHSIZE)path[i][j]=i;
				else path[i][j]=-1;
			}
		}
		for(int k=0;k<n;k++){
			for(int i=0;i<n;i++){
				if(i!=k){
					for(int j=0;j<n;j++){
						if(j!=k&&j!=i&&a[i][k]<MAXGRAPHSIZE&&a[k][j]<MAXGRAPHSIZE&&a[i][k]+a[k][j]<a[i][j]){
							a[i][j]=a[i][k]+a[k][j];
							path[i][j]=path[k][j];
						}
					}
				}
			}
		}
		//輸出
		for(int i=0;i<n;i++){
			for(int j=0;j<n;j++){
				if(i!=j&&a[j][i]<MAXGRAPHSIZE){
					System.out.println("頂點"+j+"到"+"頂點"+i+"的最短路徑長度："+a[j][i]);
					System.out.print("最短路徑為："+j);
					int k=j;
					while(path[i][k]!=i){
						System.out.print(" "+path[i][k]);
						k=path[i][k];
					}
					System.out.print(" "+i);
				}
				
			}
		}
	}
	/**
	 * 對無向加權連通圖，求最小支撐樹的prim演算法
	 */
	public void prim(){
		int n=this.graphSize;
		//權值最小的邊類
		class LV{
			int lowCost;//權值
			int vex;//邊的終點
		}
		LV[] closeEdge=new LV[n];
		//支撐樹的邊類
		class Edge{
			int head;//頭
			int tail;//尾
			int cost;//權值
		}
		Edge[] te=new Edge[n-1];
		for(int i=0;i<n;i++){
			for(int j=0;j<n;j++){
				if(edge[i][j]==0)edge[i][j]=MAXWEIGHT;
			}
		}
		//以頂點0為初始頂點,初始化陣列closeEdge
		for(int i=0;i<n;i++){
			closeEdge[i]=new LV();
			closeEdge[i].lowCost=edge[0][i]; 
			closeEdge[i].vex=0;
		}
		closeEdge[0].vex=-1;//頂點0進入集合
		int count=0;//支撐樹的邊數
		for(int i=0;i<n;i++){
			int min=MAXWEIGHT+1;
			int v=0;
			for(int j=0;j<n;j++){//求當前權值最小的邊和該邊的終點v
				if(closeEdge[j].vex!=-1&&closeEdge[j].lowCost<min){
					v=j;
					min=closeEdge[j].lowCost;
				}
			}
			//向支撐樹的邊集合中新增一條邊
			if(v!=0){
				te[count]=new Edge();
				te[count].head=closeEdge[v].vex;
				te[count].tail=v;
				te[count].cost=closeEdge[v].lowCost;
				count++;
				//頂點v進入集合U
				closeEdge[v].lowCost=0;//修改域值
				closeEdge[v].vex=-1;
				for(int j=0;j<n;j++){
					if(closeEdge[j].vex!=-1&&edge[v][j]<closeEdge[j].lowCost){
						closeEdge[j].lowCost=edge[v][j];
						closeEdge[j].vex=v;
					}
				}
			}
		}
		for(int i=0;i<n-1;i++){
			System.out.println("("+te[i].head+","+te[i].tail+","+te[i].cost+")");
		}
	}
	//測試
	public static void main(String[] args){
//      測試資料
//		0
//		2
//		7
//		1000
//		1
//		1000
//		0
//		1000
//		1000
//		1000
//		1000
//		1000
//		0
//		5
//		1000
//		1000
//		1000
//		1000
//		0
//		1000
//		3
//		1000
//		1000
//		4
//		0
		Graph_Matrix gm=new Graph_Matrix();
		System.out.println(gm.getFirstNeighbor(0));
		System.out.println(gm.getNextNeighbor(0, 1));
		gm.insertVertex();
		gm.insertEdge(5, 0, 2);
		gm.insertEdge(5, 1, 2);
		gm.insertEdge(5, 4, 2);
		System.out.println(gm.getFirstNeighbor(5));
		System.out.println(gm.getNextNeighbor(5, 0));
		gm.deleteEdge(5, 1);
		System.out.println(gm.getFirstNeighbor(5));
		System.out.println(gm.getNextNeighbor(5, 0));
		gm.deleteVertex(5);
		System.out.println(gm.getFirstNeighbor(5));
//		測試資料
//		0
//		1
//		4
//		3
//		1
//		0
//		1000
//		2
//		4
//		1000
//		0
//		5
//		3
//		2
//		5
//		0
		Graph_Matrix g=new Graph_Matrix();
		System.out.println("最小支撐樹為：");
		g.prim();
		
	}
}
 

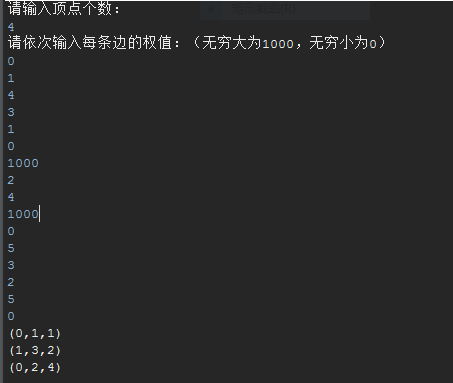
測試結果：