交併比（Intersection over Union）和非極大值抑制是（Non-Maximum Suppression）是目標檢測任務中非常重要的兩個概念。例如在用訓練好的模型進行測試時，網路會預測出一系列的候選框。這時候我們會用NMS來移除一些多餘的候選框。即移除一些IOU值大於某個閾值的框。然後在剩下的候選框中，分別計算與ground truth的IOU值，通常會規定當候選框和ground truth的IOU值大於0.5時，認為檢測正確。下面我們分別用python實現IOU和NMS。

交併比IOU

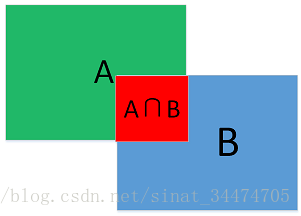
如上圖所示，IOU值定位為兩個矩形框面積的交集和並集的比值。即：

程式碼實現

import numpy as np
def compute_iou(box1, box2, wh=False):
    """
    compute the iou of two boxes.
    Args:
        box1, box2: [xmin, ymin, xmax, ymax] (wh=False) or [xcenter, ycenter, w, h] (wh=True)
        wh: the format of coordinate.
    Return:
        iou: iou of box1 and box2.
    """
 

    if wh == False:
        xmin1, ymin1, xmax1, ymax1 = box1
        xmin2, ymin2, xmax2, ymax2 = box2
    else:
        xmin1, ymin1 = int(box1[0]-box1[2]/2.0), int(box1[1]-box1[3]/2.0)
        xmax1, ymax1 = int(box1[0]+box1[2]/2.0), int(box1[1]+box1[3]/2.0)
        xmin2, ymin2 = int(box2[0]-box2[2]/2.0), int(box2[1
 
]-box2[3]/2.0)
        xmax2, ymax2 = int(box2[0]+box2[2]/2.0), int(box2[1]+box2[3]/2.0)

    ## 獲取矩形框交集對應的左上角和右下角的座標（intersection）
    xx1 = np.max([xmin1, xmin2])
    yy1 = np.max([ymin1, ymin2])
    xx2 = np.min([xmax1, xmax2])
    yy2 = np.min([ymax1, ymax2])

    ## 計算兩個矩形框面積
    area1 = (xmax1-xmin1) * (ymax1-ymin1) 
    area2 = (xmax2-xmin2) * (ymax2-ymin2)

    inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1]))　#計算交集面積
    iou = inter_area / (area1+area2-inter_area+1e-6)　＃計算交併比

    return iou

非極大值抑制（NMS）

NMS的演算法步驟如下：

# INPUT：所有預測出的bounding box (bbx)資訊（座標和置信度confidence），　IOU閾值（大於該閾值的bbx將被移除）
for object in all objects:
    (1) 獲取當前目標類別下所有bbx的資訊
    (2) 將bbx按照confidence從高到低排序,並記錄當前confidence最大的bbx
    (3) 計算最大confidence對應的bbx與剩下所有的bbx的IOU,移除所有大於IOU閾值的bbx
    (4) 對剩下的bbx，迴圈執行(2)和(3)直到所有的bbx均滿足要求（即不能再移除bbx）

需要注意的是，NMS是對所有的類別分別執行的。舉個栗子，假設最後預測出的矩形框有2類（分別為cup, pen）,在NMS之前，每個類別可能都會有不只一個bbx被預測出來，這個時候我們需要對這兩個類別分別執行一次NMS過程。
我們用python編寫NMS程式碼，假設對於一張圖片，所有的bbx資訊已經儲存在一個字典中，儲存形式如下：

predicts_dict: {"cup": [[x1_1, y1_1, x2_1, y2_1, scores1], [x1_2, y1_2, x2_2, y2_2, scores2], ...], "pen": [[x1_1, y1_1, x2_1, y2_1, scores1], [x1_2, y1_2, x2_2, y2_2, scores2], ...]}.

即目標的位置和置信度用列表儲存，每個列表中的一個子列表代表一個bbx資訊。詳細的程式碼如下：

def non_max_suppress(predicts_dict, threshold=0.2):
    """
    implement non-maximum supression on predict bounding boxes.
    Args:
        predicts_dict: {"stick": [[x1, y1, x2, y2, scores1], [...]]}.
        threshhold: iou threshold
    Return:
        predicts_dict processed by non-maximum suppression
    """
    for object_name, bbox in predicts_dict.items():   #對每一個類別的目標分別進行NMS
        bbox_array = np.array(bbox, dtype=np.float)

        ## 獲取當前目標類別下所有矩形框（bounding box,下面簡稱bbx）的座標和confidence,並計算所有bbx的面積
        x1, y1, x2, y2, scores = bbox_array[:,0], bbox_array[:,1], bbox_array[:,2], bbox_array[:,3], bbox_array[:,4]
        areas = (x2-x1+1) * (y2-y1+1)
        #print "areas shape = ", areas.shape

        ## 對當前類別下所有的bbx的confidence進行從高到低排序（order儲存索引資訊）
        order = scores.argsort()[::-1]
        print "order = ", order
        keep = [] #用來存放最終保留的bbx的索引資訊

        ## 依次從按confidence從高到低遍歷bbx，移除所有與該矩形框的IOU值大於threshold的矩形框
        while order.size > 0:
            i = order[0]
            keep.append(i) #保留當前最大confidence對應的bbx索引

            ## 獲取所有與當前bbx的交集對應的左上角和右下角座標，並計算IOU（注意這裡是同時計算一個bbx與其他所有bbx的IOU）
            xx1 = np.maximum(x1[i], x1[order[1:]])　#當order.size=1時，下面的計算結果都為np.array([]),不影響最終結果
            yy1 = np.maximum(y1[i], y1[order[1:]])
            xx2 = np.minimum(x2[i], x2[order[1:]])
            yy2 = np.minimum(y2[i], y2[order[1:]])
            inter = np.maximum(0.0, xx2-xx1+1) * np.maximum(0.0, yy2-yy1+1)
            iou = inter/(areas[i]+areas[order[1:]]-inter)
            print "iou =", iou

            print np.where(iou<=threshold) #輸出沒有被移除的bbx索引（相對於iou向量的索引）
            indexs = np.where(iou<=threshold)[0] + 1 #獲取保留下來的索引(因為沒有計算與自身的IOU，所以索引相差１，需要加上)
            print "indexs = ", type(indexs)
            order = order[indexs] #更新保留下來的索引
            print "order = ", order
        bbox = bbox_array[keep]
        predicts_dict[object_name] = bbox.tolist()
        predicts_dict = predicts_dict
    return predicts_dict

假設我們現在已經計算得到了網路輸出的bbx資訊如下：

predict dict =  {'cup': [[59, 120, 137, 368, 0.124648176], [221, 89, 369, 367, 0.35818103], [54, 154, 148, 382, 0.13638769]]}

即模型已經預測出了三個bbx，我們看一下在原圖上的結果：

我們呼叫上面的non_max_suppress函式，並使用預設閾值，再看處理後的結果：

可以發現，多餘的bbx已經被抑制了。