雅可比迭代法法

在圖形影象中很多地方用到求矩陣的特徵值和特徵向量，比如主成分分析、OBB包圍盒等。程式設計時一般都是用數值分析的方法來計算，這裡介紹一下雅可比迭代法求解特徵值和特徵向量。雅可比迭代法的原理，網上資料很多，詳細可見參考資料1。這裡我們簡單介紹求解矩陣S特徵值和特徵向量的步驟：

1. 初始化特徵向量為對角陣V，即主對角線的元素都是1.其他元素為0。
2. 在S的非主對角線元素中，找到絕對值最大元素 Sij。
3. 用下 式計算tan2θ，求 cosθ、sinθ 及旋轉矩陣Gij 。
   
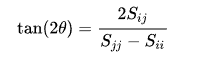
4. 用下面公式求S‘；用當前特徵向量矩陣V乘以矩陣Gij得到當前的特徵向量V。
   
5. 若當前迭代前的矩陣A的非主對角線元素中最大值小於給定的閾值e時，停止計算；否則, 令S =S‘, 重複執行(2) ~ (5)。 停止計算時，得到特徵值 li≈(S‘) ij ，i,j= 1,2,…,n.以及特徵向量V。
6. 這一步可選。根據特徵值的大小從大到小的順序重新排列矩陣的特徵值和特徵向量。

程式碼實現

用C++實現，並與參考資料1示例對比。

#include <iostream>
#include <map>
#include<math.h>
#include <iomanip>
using namespace std;

/**
* @brief                        Jacobi eigenvalue algorithm
* @param matrix				    n*n array
* @param dim					dim represent n
* @param eigenvectors			n*n array
* @param eigenvalues			n*1 array
* @param precision   			precision requirements
* @param max					max number of iterations
* @return
*/
bool Jacobi(double* matrix, int dim, double* eigenvectors, double* eigenvalues, double precision, int max)
{
	for (int i = 0; i < dim; i++) {
		eigenvectors[i*dim + i] = 1.0f;
		for (int j = 0; j < dim; j++) {
			if (i != j)
				eigenvectors[i*dim + j] = 0.0f;
		}
	}

	int nCount = 0;		//current iteration
	while (1) {
		//find the largest element on the off-diagonal line of the matrix
		double dbMax = matrix[1];
		int nRow = 0;
		int nCol = 1;
		for (int i = 0; i < dim; i++) {			//row
			for (int j = 0; j < dim; j++) {		//column
				double d = fabs(matrix[i*dim + j]);
				if ((i != j) && (d > dbMax)) {
					dbMax = d;
					nRow = i;
					nCol = j;
				}
			}
		}

		if (dbMax < precision)     //precision check 
			break;
		if (nCount > max)       //iterations check
			break;
		nCount++;

		double dbApp = matrix[nRow*dim + nRow];
		double dbApq = matrix[nRow*dim + nCol];
		double dbAqq = matrix[nCol*dim + nCol];
		//compute rotate angle
		double dbAngle = 0.5*atan2(-2 * dbApq, dbAqq - dbApp);
		double dbSinTheta = sin(dbAngle);
		double dbCosTheta = cos(dbAngle);
		double dbSin2Theta = sin(2 * dbAngle);
		double dbCos2Theta = cos(2 * dbAngle);
		matrix[nRow*dim + nRow] = dbApp*dbCosTheta*dbCosTheta +
			dbAqq*dbSinTheta*dbSinTheta + 2 * dbApq*dbCosTheta*dbSinTheta;
		matrix[nCol*dim + nCol] = dbApp*dbSinTheta*dbSinTheta +
			dbAqq*dbCosTheta*dbCosTheta - 2 * dbApq*dbCosTheta*dbSinTheta;
		matrix[nRow*dim + nCol] = 0.5*(dbAqq - dbApp)*dbSin2Theta + dbApq*dbCos2Theta;
		matrix[nCol*dim + nRow] = matrix[nRow*dim + nCol];

		for (int i = 0; i < dim; i++) {
			if ((i != nCol) && (i != nRow)) {
				int u = i*dim + nRow;	//p  
				int w = i*dim + nCol;	//q
				dbMax = matrix[u];
				matrix[u] = matrix[w] * dbSinTheta + dbMax*dbCosTheta;
				matrix[w] = matrix[w] * dbCosTheta - dbMax*dbSinTheta;
			}
		}

		for (int j = 0; j < dim; j++) {
			if ((j != nCol) && (j != nRow)) {
				int u = nRow*dim + j;	//p
				int w = nCol*dim + j;	//q
				dbMax = matrix[u];
				matrix[u] = matrix[w] * dbSinTheta + dbMax*dbCosTheta;
				matrix[w] = matrix[w] * dbCosTheta - dbMax*dbSinTheta;
			}
		}

		//compute eigenvector
		for (int i = 0; i < dim; i++) {
			int u = i*dim + nRow;		//p   
			int w = i*dim + nCol;		//q
			dbMax = eigenvectors[u];
			eigenvectors[u] = eigenvectors[w] * dbSinTheta + dbMax*dbCosTheta;
			eigenvectors[w] = eigenvectors[w] * dbCosTheta - dbMax*dbSinTheta;
		}
	}

	//sort eigenvalues
	std::map<double, int> mapEigen;
	for (int i = 0; i < dim; i++) {
		eigenvalues[i] = matrix[i*dim + i];
		mapEigen.insert(make_pair(eigenvalues[i], i));
	}

	double *pdbTmpVec = new double[dim*dim];
	std::map<double, int>::reverse_iterator iter = mapEigen.rbegin();
	for (int j = 0; iter != mapEigen.rend(), j < dim; ++iter, ++j)	{
		for (int i = 0; i < dim; i++) {
			pdbTmpVec[i*dim + j] = eigenvectors[i*dim + iter->second];
		}
		eigenvalues[j] = iter->first;
	}

	for (int i = 0; i < dim; i++) {
		double dSumVec = 0;
		for (int j = 0; j < dim; j++)
			dSumVec += pdbTmpVec[j * dim + i];
		if (dSumVec < 0) {
			for (int j = 0; j < dim; j++)
				pdbTmpVec[j * dim + i] *= -1;
		}
	}
	memcpy(eigenvectors, pdbTmpVec, sizeof(double)*dim*dim);
	delete[]pdbTmpVec;
	return true;
}


int main()
{
	double a[4][4] = { {4, -30, 60, -35}, {-30, 300, -675, 420},{ 60, -675, 1620, -1050},{ -35, 420, -1050, 700}};
	int n = 4;
	double eps = 1e-10;
	int T = 10000;
	double p[4][4] = { 0 };
	double v[4] = { 0 };
	bool re = Jacobi(&a[0][0], n, &p[0][0], v, eps, T);
	if (re)	{
		cout << "Matrix:" << endl;
		for (int i = 0; i < n; i++)	{
			for (int j = 0; j < n; j++)
				cout << setw(15) << a[i][j];
			cout << endl;
		}
		cout << "eigenvectors:" << endl;
		for (int i = 0; i < n; i++)	{
			for (int j = 0; j < n; j++)
				cout << setw(15) << p[i][j];
			cout << endl;
		}
		cout << "eigenvalues:" << endl;
		for (int i = 0; i < n; i++)	{
				cout << setw(15) << v[i];
			cout << endl;
		}
	}
	else
		cout << "false" << endl;
	system("pause");
}
 

執行結果：

參考資料1示例結果：

參考資料

【Jacobi eigenvalue algorithm】https://en.wikipedia.org/wiki/Jacobi_eigenvalue_algorithm