線性代數筆記22——特徵值和特徵向量
特徵向量
函式通常作用在數字上,比如函式f作用在x上,結果得到了f(x)。線上性代數中,我們將x擴充套件到多維,對於Ax來說,矩陣A的作用就像一個函式,輸入一個向量x,通過A的作用,得到向量Ax。對多數向量x而言,經過Ax的轉換後將得到不同方向的向量,但總有一些特殊的向量,它的方向和Ax方向相同,即Ax平行於x,這些特殊的向量就是特徵向量。
平行的向量用方程來表示比較簡單:
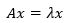
其中A是方陣,x≠0。λ是一個係數,被稱為特徵係數或特徵值;x和λx平行,方程的解x就是A的特徵向量。
這裡需要對“方向相同”做出一些特殊的解釋,它也包括正好相反的方向和無方向,所以λ的值可以取0或負數。
求解特徵向量
現在的問題是,給定矩陣A,如果求解A的特徵向量?這裡沒有Ax = b這樣的方程,只有Ax=λx,其中λ和x都是未知數,如何求解呢?在解釋之前,先看看投影矩陣的特徵向量。
投影矩陣的特徵向量
假設有個一個平面,給定投影矩陣P,投影矩陣的特徵向量有哪些?特徵值又是什麼?
這實際上是在回答那些向量的投影和向量本身平行,像下面這樣隨意投影肯定不行:
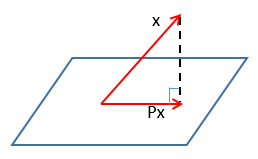
x在平面的投影是Px,二者的方向不相同,因此圖中的x不是P的特徵向量。
如果x正好在平面上,那麼它的投影就是x本身,所以位於平面上的所有向量都是P的特徵向量,此時特徵值λ=1,Px=x。此外,垂直於平面的向量在平面上的投影是零向量,即Px = 0 = 0x,這相當於特徵值λ=0,所以垂直於平面的向量也是P的特徵向量。
矩陣的跡
再看一個特例:

A乘以什麼樣的向量將得到一個同方向的向量?即A的特徵值和特徵向量是什麼?
很容易看出:
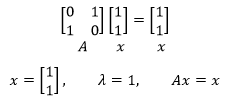
A還有其它的特徵值:

上面的答案符合兩個關於特徵值的性質:
- n×n矩陣有n個特徵值。
- 矩陣的所有特徵值之和等於該矩陣的主對角線元素之和,這個和數叫做A的跡。
特徵方程
現在到了面對Ax=λx的時候,弄清楚如何求解λ和x。
解決的方法是將λx移到等式左側:
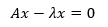
更進一步,可以利用λx = λIx將λ向量化,變成:
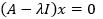
複習一下零空間,對於Ax = 0來說,如果A的各列是線性無關的,意味著方程組只有一個全零解。把這句話放到新方程中,如果(A-λI) 的各列是線性無關的,意味著只有一個解,x=0。但是特徵向量不能是零向量,所以需要新方程還有其它解,這意味著(A-λI) 的各列是線性相關的,即A-λI是一個奇異矩陣。由於奇異矩陣的行列式是0,因此可以得到結論:
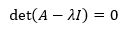
這就沒x什麼事了,得到了一個關於λ的方程,該方程叫做特徵方程或特徵值方程。可以根據特徵方程先求解出λ,當然,對於n階方陣會求出n個λ。知道λ後就容易多了,把每個λ代入(A-λI)x=0,然後找出它的零空間。(關於零空間,可參考《線性代數筆記12——列空間和零空間》)
來看一個示例:
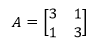
先求解A的特徵值:
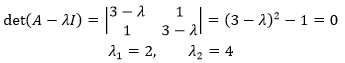
A的跡是所有特徵值之和,它等於主對角線元素之和,這可以用來作為特徵值求解的初步驗證。接下來求解每個特徵值對應的特徵向量:
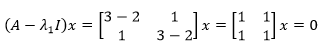
容易判斷零空間的基是:

這也是特徵值λ1對應的特徵向量,實際上零空間中的所有向量都是λ1對應的特徵向量。
用同樣的方法求出λ2對應的特徵向量:
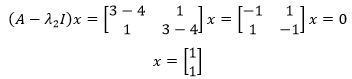
複數特徵值
值得注意的是,特徵值未必是實數,比如下面的矩陣:
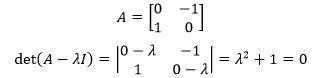
此時特徵值是複數,λ=±i
綜合示例
召喚一個矩陣A:
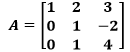
找出A,A2,A-1的特徵值和特徵向量。
先看簡單的,求解A的特徵值比較容易:

第一列中有兩個0,所以將這個行列式以第一列展開:

三個特徵值之和等於A的主對角元素之和。
接下來求解特徵值:
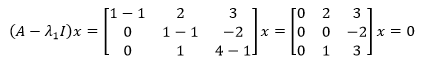
方程的一組解就是特徵向量:
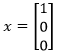
接下來求出另外兩個特徵向量:
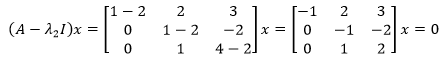
找出對應的零空間,先化簡為行階梯矩陣:
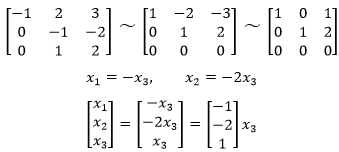
當x3 = 1時,將得到一組特徵向量:
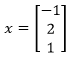
繼續計算λ3的特徵向量:

當x3 = 1時,將得到一組特徵向量:
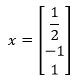
接下來計算A2的特徵值,這將是個浩大的工程,我們更想讓它變得容易一點,已知Ax=λx,現在將A再左乘一個A變成A2:
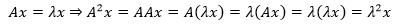
等式的源頭是Ax=λx,假設x是已知的,它已經被求得,因此這個式子告訴我們,如果已知A的特徵向量,那麼它也是A2的特徵向量,只不過特徵值換成了λ2。
類似地,A-1x也可以做一些演變:
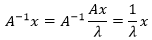
A-1的特徵值就是1/λ,,它的特徵值和A的特徵值相同。
作者:我是8位的
出處:http://www.cnblogs.com/bigmonkey
本文以學習、研究和分享為主,如需轉載,請聯絡本人,標明作者和出處,非商業用途!
掃描二維碼關注公眾號“我是8位的”

出處:http://www.cnblogs.com/bigmonkey
本文以學習、研究和分享為主,如需轉載,請聯絡本人,標明作者和出處,非商業用途!
掃描二維碼關注公眾號“我是8位的”

