在R中進行相關分析
阿新 • • 發佈:2019-01-07
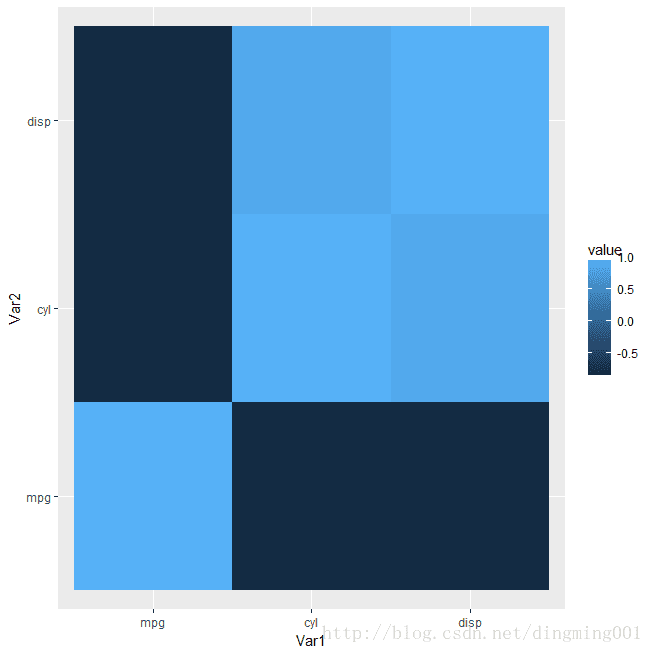
1.用R進行多元相關分析
#用cov函式計算mtcars資料框的前三個變數的協方差矩陣
> cov(mtcars[1:3])
mpg cyl disp
mpg 36.324103 -9.172379 -633.0972
cyl -9.172379 3.189516 199.6603
disp -633.097208 199.660282 15360.7998
#用cor函式計算mtcars資料框的前三個變數的相關係數矩陣
> cor(mtcars[1:3])
mpg cyl disp 2.進行多元線性迴歸分析
#...
>data(mtcars)
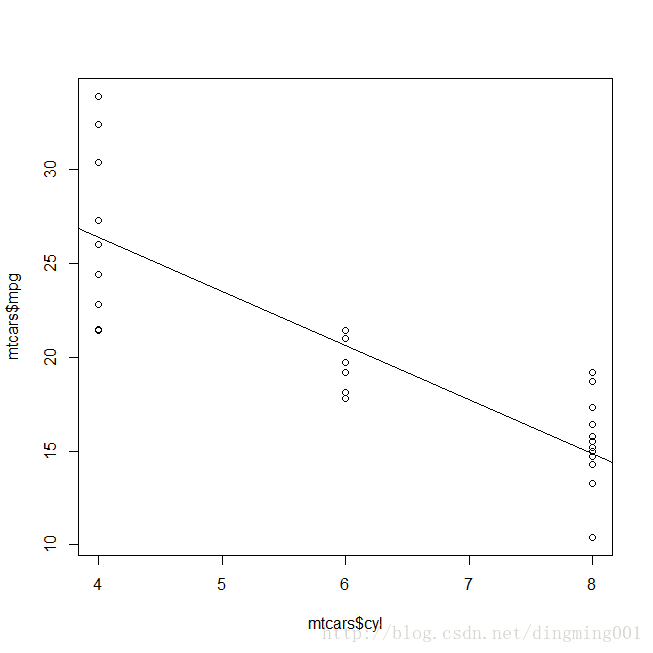
#呼叫lm函式將變數裝入線性模型中
> lmfit = lm(mtcars$mpg ~ mtcars$cyl)
> lmfit
Call:
lm(formula = mtcars$mpg ~ mtcars$cyl)
Coefficients:
(Intercept) mtcars$cyl
37.885 -2.876
#呼叫summary函式獲得模型的特徵資訊:
Estimate Std. Error t value Pr(>|t|)
估值,標準誤差,T值,P值
Call:
lm(formula = mtcars$mpg ~ mtcars$cyl)
Residuals:
Min 1Q Median 3Q Max