最短路徑 輸出路徑 Dijkstra演算法
某個源點到其餘各頂點的最短路徑
這個演算法最開始心裡怕怕的,不知道為什麼,花了好長時間弄懂了,也寫了一遍,又遇到時還是出錯了,今天再次寫它,心裡沒那麼怕了,耐心研究,懂了之後會好開心的,哈哈
Dijkstra演算法:
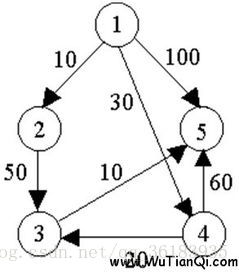
圖G
如圖:若要求從頂點1到其餘各頂點的最短路徑,該咋求;
迪傑斯特拉提出“按最短路徑長度遞增的次序”產生最短路徑。
首先,在所有的這些最短路徑中,長度最短的這條路徑必定只有一條弧,且它的權值是從源點出發的所有弧上權的最小值,例如:在圖G中,從源點1出發有3條弧,其中以弧(1,2)的權值為最小,因此,(1,2)不僅是1到2的一條最短路徑,並且它可能是源點到其它各個終點的最短路徑中的一條子路徑。
其次,第二條長度次短的最短路徑只可能有兩種情況:①它或者只含一條從源點出發的弧且弧上的權值大於已求得最短路徑的那條弧的權值,但小於其他從源點出發的弧上的權值②它或者是一條只經過已求得最短路徑的頂點的路徑。
例如圖G中,從1到其他各點。過程中,用d[i]儲存從1到i的的最短路徑(過程會變化),初值為:若源點到該源點有弧,則為權值,否則初始化為無窮大,每求得一條到達某個終點i的最短路徑,就繼續檢查是否存在以此路徑為子路徑的到達其他點的最短路徑,若存在,判斷其長度是否比當前求得的路徑長度短,若短,就更新為更短的長度。
如圖G中,求得到2的最短路徑d[2]為10,就把d[2]作為與2相連的到其他點的子路徑
過程:
(1).令S={1},S集合中表示已經找到最短路徑的結點,開始時1為源點,並設定d[i]的初始值為:d[i]=(1,i),
(2).求出到j點的最短路徑,j點為不在S集合中的某點
d[j]=min{d[i]}
(3).判斷所有沒在S集合中的頂點k,若d[k]>d[j]+(j,k)則修改d[k]的值為:
d[k]=d[j]+(j,k)
(4).重複(2).(3)操作共n-1次,每次操作,在(2)得到一個到
某點的最短路徑。
有向圖求最短路徑
#include<stdio.h>
#include<string.h> 無向圖求最短路徑
無向圖也是相同思路:在構造鄰接矩陣時考慮對稱就行。
無向圖求最短路徑且有路徑輸出
在求最短路的過程中,最短路①它或者是從源點出發的弧②它或者是一條經過已到其他最短路徑的頂點的路徑。
建立一個新的結構體型別path,該型別變數d表示到達某點的最短路徑距離 ,該型別變數pre表示該最短路徑是經過哪個點傳過來的
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define max 900000000
typedef struct{
int d;//到達某點的最短路徑距離
int pre;//該最短路徑是經過哪個點傳過來的,源點或其他某個點
}path;
//有向圖
int main(){
int n,m,a,b,v,i,j,min,k,from;
scanf("%d%d",&n,&m);//輸入n個頂點,m條邊
int g[n+1][n+1],vis[n+1];//g[i][j]表示i到j的邊的權值,vis[i]表示到此頂點的最短路是否已經找到,d[i]當前源點到i頂點的最短路徑
path to[n+1];//記錄當前到某個點的最短路徑以及從哪個點傳過來的
memset(vis,0,sizeof(vis));
for(i=0;i<=n;i++){
for(j=0;j<=n;j++){
g[i][j]=max;
}
to[i].d=max;
}
for(i=0;i<m;i++){//i到j的邊權值儲存到g陣列中,i點到j點無直接相連的邊時,g[i][j]=max
scanf("%d%d%d",&a,&b,&v);
g[a][b]=v;
g[b][a]=v;
}
for(i=2;i<=n;i++){
to[i].d=g[1][i]; //初始化源點到i點邊權值,之後過程中會發生變化
if(g[1][i]!=max){
to[i].pre=1;
}
}
vis[1]=1;
for(i=2;i<=n;i++){//共迴圈n-1次,每迴圈一次,確定一條最短路,再次迴圈時這條路就不用考慮了,去尋找下一條最短路
min=max;
for(j=2;j<=n;j++){//尋找下一條當前最短路
if(to[j].d<min&&vis[j]==0){
min=to[j].d;
k=j;
}
}
vis[k]=1;//找到了,到k點的路是當前最短路,標記它,根據它尋找下一條最短路
for(j=2;j<=n;j++){
if(to[j].d>to[k].d+g[k][j]&&vis[j]==0){//經過此k點到達j點的路徑是否小於其他到達j點的路徑
to[j].d=to[k].d+g[k][j];
to[j].pre=k;//改變j點是誰傳來的,現在到j點的最短路徑是經過k點的,由j點傳來
}
}
}
for(i=2;i<=n;i++){//輸出到達個點的最短路徑
printf("%d ",to[i].d);
printf("%d ",i);
j=i;
while(j!=1){
j=to[j].pre;
printf("%d ",j);
}
printf("\n");
}
return 0;
}