《實時碰撞檢測演算法技術》讀書筆記(六):最近點計算(下)
點至3D矩形的最近點
實際上等同於計算OBB上的最近點,其中3D矩形可看做是z向為0的OBB。
struct Rect {
Point c;
Vector u[2];
float e[2];
}令z軸為0並重寫函式ClosestPtPointOBB()
//Given point p, return point q on (or in) Rect r, closest to p void ClosestPtPointRect(Point p, Rect r, Point &q) { Vector d = p - r.c; //Start result at center of rect; make steps from there q = r.c; //For each rect axis... for(int i = 0; i < 2; i++) { //...project d onto that axis to get the distance //along the axis of d from the rect center float dist = Dot(d, r.u[i]); //if distance farther than the rect extents, clamp to the box if(dist > r.e[i]) dist = r.e[i]; if(disr < -r.e[i]) dist = -r.e[i]; //Step that distance along the axis to get world coordinate q += dist * r.u[i]; } }
點至三角形的最近點
給定三角形ABC以及一點P,且令ABC上距P的最近點為Q。一種解決方案是:如果P正交投影后位於三角形內部,則投影點即為最近點Q,如果P的正交投影位於三角形ABC的外部,則最近點位於三角形的某一邊上。此時則遍歷每一條邊(AB、BC、CA),計算並返回P的最近點。但明顯此種方法並不高效。一種較好的演算法是:考查P位於三角形的哪一個Voronoi特徵域中。一旦確定,只須將P正交投影至該特徵域中即可獲取最近點Q。
P位於包含頂點A的Voronoi域由穿越A的兩個平面的負半空間的交集構成,其法線分別為B-A和C-A。
確定P位於某一邊的Voronoi域,可以採用:計算P在ABC
若點P不屬於任一頂點或邊的Voronoi域,則Q必位於三角形ABC的內部,實際上為正交投影R。

P點在ABC上正交投影的質心座標為三角形RAB、RBC和RCA的有符號面積與三角形ABC有符號面積之比。令n為三角形ABC的法線,且對於某t值,有R = P - tn,則R = uA + vB + wC的質心座標(u,v,w)為:u = rbc/abc, v = rca/abc以及w = rab/abc。通過某些向量計算,可以達到一定程度上的簡化目的。如,表示式rab可以按如下方式進行簡化:
Vector n = Cross(b - a, c - a);
float rab = Dot(n, Cross(a - r, b - r)); //proportional to signed area of RAB
float rbc = Dot(n, Cross(b - r, c - r)); //proportional to signed area of RBC
float rca = Dot(n, Cross(c - r, a - r)); //proportional to signed area of RCA
float abc = rab + rbc + rca; //proportional to signed of ABC
(上面程式碼中,n應該為垂直於三角形的向量(法線)。Cross代表叉乘,設α為a,b夾角,則Cross(a,b)的數學意義是absinα*n。而三角形中,若已知兩邊及它們的夾角α,其面積則是0.5*absinα。即三角形ABC的面積=1/2*abs(AB×AC))
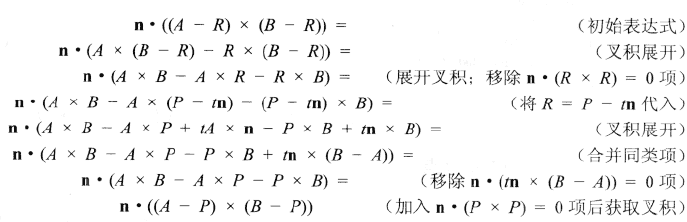
即R的質心座標可以直接通過P獲得,而無須計算R。
於是,首先判斷P點是否在三角形3個頂點域內,是則取該頂點為最近點,否則繼續判斷是否在邊域內,若在邊域內,取投影在邊上的點,否則位於三角形內部,取正交投影座標R。
(
對下面部分程式碼的解釋:
點投影在直線上:P’ = A + s*AB, s = snom/(snom + sdenom),(snom + sdenom)指AB長度,snom指投影到AB上的長度AP’(snom負表示PA與AB角度大於90度)。
面與面之間夾角:float vc = Dot(n, Cross(a - p, b - p)),vc負表示面之間夾角大於90度。
)
Point ClosestPtPointTriangle(Point p, Point a, Point b, Point c)
{
Vector ab = b - a;
Vector ac = c - a;
Vector bc = c - b;
//Compute parametric position s for projection P’ for P on AB.
//P’ = A + s*AB, s = snom/(snom + sdenom)
float snom = Dot(p - a, ab), sdenom = Dot(p - b, a - b);
//Compute parametric position t for projection P’ of P on AC,
//P’ = A + t*AC, t = tnom/(tnom + tdenom)
float tnom = Dot(p - a, ac), tdenom = Dot(p - c, a - c);
if(snom <= 0.0f && tnom <= 0.0f) return a; //Vertex region early out
//Compute parametric position u for projection P’ of P on BC,
//P’ = B + u*BC, u = unom/(unom + udenom)
float unom = Dot(p - b, bc), udenom = Dot(p - c, b - c);
if(sdenom <= 0.0f && unom <= 0.0f) return b; //Vertex region early out
if(tdenom <= 0.0f && udenom <= 0.0f) return c; //Vertex region early out
//P is outside (or on) AB if the triple scalar product [N PA PB] <= 0
Vector n = Cross(b - a, c - a);
float vc = Dot(n, Cross(a - p, b - p));
//If P outside AB and within feature region of AB,
//return projection of P onto AB
if(vc <= 0.0f && snom >= 0.0f && sdenom >= 0.0f)
return a + snom / (snom + sdenom) * ab;
//P is outside (or on) BC if the triple scalar product [N PB PC] <= 0
float va = Dot(n, Cross(b - p, c - p));
//If P outside BC and within feature region of BC,
//return projection of P onto BC
if(va <= 0.0f && unom >= 0.0f && udenom >= 0.0f)
return b + unom / (unom + udenom) * bc;
//P is outside (or on) CA if the triple scalar product [N PC PA] <= 0
float vb = Dot(n, Cross(c - p, a - p));
//If P outside CA and within feature region of CA,
//return projection of P onto CA
if(vb <= 0.0f && tnom >= 0.0f && tdenom >= 0.0f)
return a + tnom / (tnom + tdenom) * ac;
//P must project inside face region. Compute Q using barycentric coordinates
float u = va / (va + vb + vc);
float v = vb / (va + vb + vc);
float w = 1.0f - u - v; // = vc / (va + vb + vc)
return u * a + v * b + w * c;
}以上程式碼呼叫了4次叉積運算。與點積運算相比,叉積運算通常成本較高。因此,採用某種更加經濟的表示式是值得考慮的。根據拉格朗日恆等式:
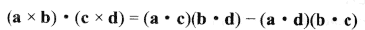
可表示3個標量三重積:
Vector n = Cross(b - a, c - a);
float va = Dot(n, Cross(b - p, c - p));
float vb = Dot(n, Cross(c - p, a - p));
float vc = Dot(n, Cross(a - p, b - p));
並利用6個點積計算對以下內容進行表達:
float d1 = Dot(b - a, p - a);
float d2 = Dot(c - a, p - a);
float d3 = Dot(b - a, p - b);
float d4 = Dot(c - a, p - b);
float d5 = Dot(b - a, p - c);
float d6 = Dot(c - a, p - c);
最終有:
float va = d3 * d6 - d5 * d4;
float vb = d5 * d2 - d1 * d6;
float vc = d1 * d4 - d3 * d2;
實際上,d1~d6也可以用於計算snom、sdenom、tnom、tdenom、unom以及udenom:
float snom = d1;
float sdenom = -d3;
float tnom = d2;
float tdenom = -d6;
float unom = d4 - d3;
float udenom = d5 - d6;
其中向量n不再需要。
點到四面體的最近點
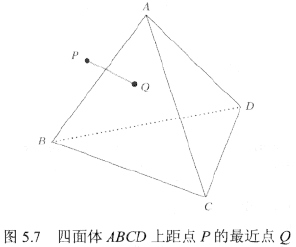
給定點P,當前問題為:計算四面體ABCD上(或之內)距離點P的最近點Q。一種較為直接的演算法是:針對四面體中的每一個面,呼叫函式ClosestPointTriangle()並計算最近點。在多個計算結果中,返回距點P最近的點Q。獨立於距離測試,還需要考查點P是否位於四面體中的面內。若P位於四面體中某一面內,則其即為最近點。
//Test if point and d lie on opposite side of plane through abc
int PointOutsideOfPlane(Point p, Point a, Point b, Point c, Point d)
{
float signp = Dot(p - a, Cross(b - a, c - a)); //[AP AB AC]
float signd = Dot(d - a, Cross(b - a, c - a)); //[AD AB AC]
//Points on opposite sides if expression signs are opposite
return signp * signd < 0.0f;
}上訴演算法執行良好且易於實現。然而該演算法仍有改進餘地。首先,假定頂點P的Voronoi特徵域存在,則Q為P在該正交域上的正交投影。針對四面體,需要考查總計14個特徵域:4個頂點域、6個邊域以及4個面域。若P不屬於任何一個特徵域,則必定位於四面體內部。
與前述測試方法相比,該演算法似乎無明顯的效能改觀。然而,Voronoi域間卻可以共享多數計算過程而無須重複計算。
點到凸多面體的最近點
一種易於實現的、複雜度為O(n)的演算法是:計算多面體上每個面中距P的最近點,並返回一個最近結果。同時,還要兼顧測試點P是否位於H各面的背面,即P位於H內部這一情況。為了加速測試過程,面距離測試計算規定:點P位於各面的正面。
對於較大的多面體,一種較為快速的預計算方法為:以層次結構的方式構建多面體的各部分。利用這種預構造的層級方案將使最近點計算的時間複雜度達到log級別。如Dobkin-Kirkpatrick層次結構演算法。
此外還有一些高效計算多面體最近點的其他一些演算法如GJK演算法等。
兩直線間的最近點
對於2D空間,兩直線不平行則相交,相交時最近點為交點,平行時的最近點為線上任意點。而在3D空間中則未必。故在3D空間中一個較好方案是:若兩直線之間彼此並未達到足夠接近,則設為不相交(未必平行)。基於此,相交測試轉換為兩直線間之間的距離,並檢測該距離是否小於給定的閥值。
給定L1由頂點Q1,P1連成,L2由頂點Q2,P2連成。
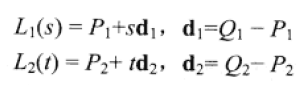
針對s和t的幾組計算結果,L1(s)l和L2(t)分別對應直線上的最近點,且v(s, t) = L1(s) - L2(t)。當v具有最小長度值時,兩頂點則為最近點。其實即為計算s和t滿足以下垂直約束條件:
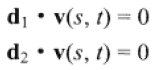
在此省略推導給出結果:
設a = d1·d1, b = d1·d2, c = d1·r, e = d2·d2, f = d2·r, d = ae - b^2
則s = (bf - ce) / d t = (af - bc) / d
注意:當d=0時兩直線平行且需要另行處理。
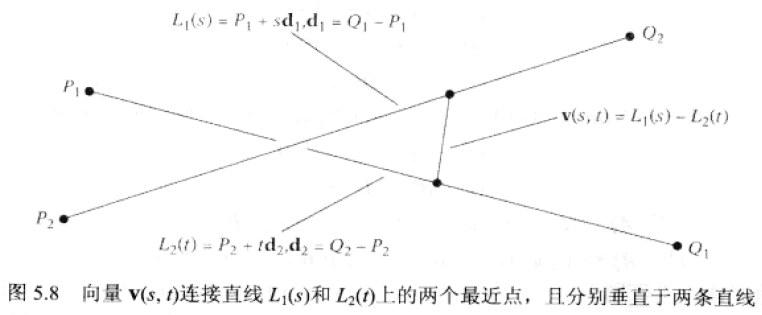
兩線段上的最近點
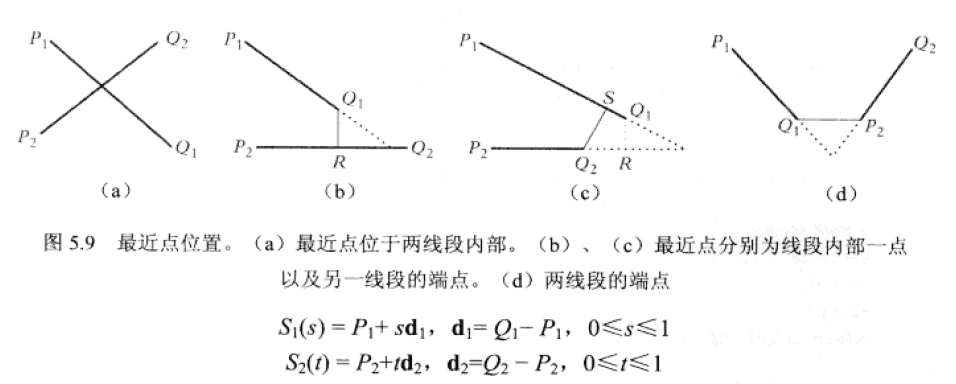
不難看出,在某些情況下,若直線間某一最近點位於相關線段的外部延長線上,該點是可以擷取至相應線段的最近端點處。
若直線間的最近點皆位於各自線段的外部延長線上,則上述擷取操作需要重複計算兩次。
給定直線上L2一點S2(t) = P2 + td2,則L1上最近點L1(s)為:
s = (S2(t) - P1)·d1/d1·d1 = (P2 + td2 - P1)·d1/d1·d1
類似地,給定直線S1上一點S1(s) = P1 + sd1,直線L2上最近點L2(t)為:
t = (S1(s) - P2)·d2/d2·d2 = (P1 + sd1 - P2)·d2/d2·d2
可以使用高斯消元法求解線性方程組。
s = (bt - c)/a
t = (bs + f)/e
其中,a = d1·d1, b = d1·r, e = d2·d2, f = d2·r
2D線段相交計算
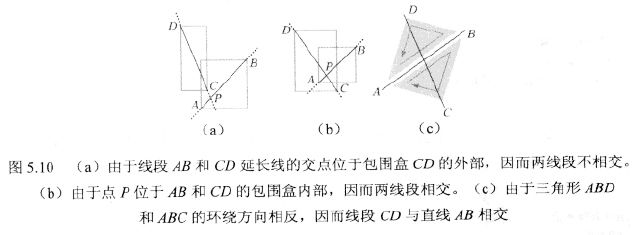
測試兩線段AB、CD是否相交,可以首先計算二者(延長線)的交點,且檢視該交點是否位於各自線段的包圍盒中。需注意的是,需要單獨處理兩線段平行這一特例。
計算兩線段(延長線)交點時,顯式定義直線L1的方程L1(t) = A + t(B - A),並隱式定義另一直線方程n·(X - C) = 0,其中n 垂直於CD。利用A+t(B - A)帶入方程n·(X - C) = 0並求解t:

則交點P = L1(t)可將t值代入上述顯式方程得到。另外,可通過檢測0<=t<=1從而確定P是否位於AB包圍盒內。
另一種2D線段相交測試方案為:兩線段相交僅當兩端點彼此位於線段兩側。可以通過判斷三角形ABD和ABC的環繞方向加以解決,而三角形的有符號面積可以確定其環繞方向(|a × b| = |a||b|sino,設點a(x1,y1), b(x2, y2)夾角為o則|a||b|sino = |x1y2 - x2y1|,可得三角形有符號面積為0.5*(x1y2 - x2y1)。 兩個非零向量a和b平行,當且僅當|a × b|= 0)。對於某些應用,可以在執行線段相交測試前線處理線段的AABB盒相交測試。對於3D空間內成本高昂的線段相交測試,這一點尤為重要。
//Return 2 times the signed triangle area. The result is positive if
//abc is ccw, negative if abc is cw, zero if abc is degenerate.
float Signed2DTriArea(Point a, Point b, Point c) {
return (a.x - c.x) * (b.y - c.y) - (a.y - c.y) * (b.x - c.x);
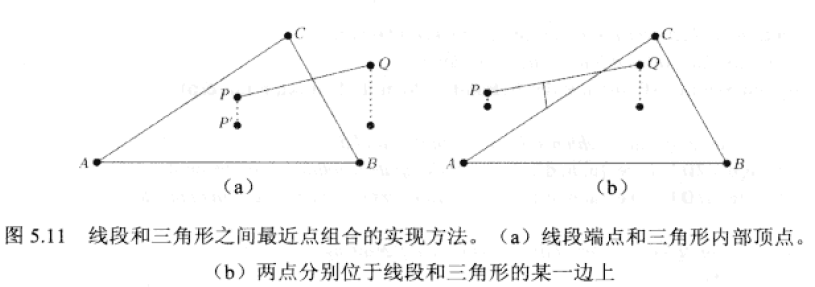
}線段和三角形最近點
在此不討論平行情況。
最近點計算涉及下列物件:
線段PQ與三角形邊AB
線段PQ與三角形邊BC
線段PQ與三角形邊CA
線段端點P與三角形平面(P的投影位於三角形ABC內)
線段端點Q與三角形平面(Q的投影位於三角形ABC內)
上述計算返回具有唯一最小距離的最近點作為結果。
在某些情況下,可以適當調整測試的數量以減少計算量。如,若線段兩端點投影均位於三角形內部,則無需再執行線段-邊的最近點測試,因為最近點必然產生於線段的某一投影點中;若只是線段的一個端點投影位於三角形內部,則只須執行一次相應的線段-邊測試;當線段的投影均位於三角形外部,也只須執行一次相應的線段-邊測試。對於後兩種情況,可以通過計算線段端點所處的Voronoi域確定相關的線段-邊測試。
兩個三角形之間的最近點計算
兩個三角形T1和T2之間的最近點計算一般可認為:相應最近點位於某一個三角形的邊上。因此,其結果轉化成可對三角形中6條邊之間的可能組合,執行線段-三角形的最近點計算。則包含最小(平方)距離的一組點即為最近點集合。
但線段-三角形之間距離測試成本較高。一種較好T1,T2間最近點集測試方案為:一組最近點產生於兩個三角形的相應邊上,或產生於某一頂點與另一個三角形的內部點之間。問題轉化成:計算兩三角形間一對邊的最近距離,以及頂點與三角形之間的最近點(相應頂點的投影位於三角形內部)。綜上,需要執行6次頂點-三角形測試以及9次邊-邊測試。最終從多組最近點中,選擇具有最小距離的一組頂點作為最終三角形間的最近點。
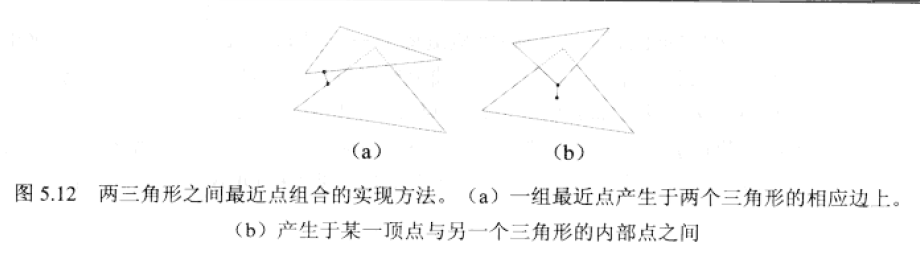
(三角形平行以及重合的情況需要剔除)