AI從入門到放棄之特徵工程
阿新 • • 發佈:2019-01-07
特徵工程
俗話說,“巧婦難為無米之炊”,機器學習中,資料和特徵便是“米”,模型和演算法則是“巧婦”。對於一個機器學習問題,資料和特徵往往決定了結果的上限,而模型、演算法的選擇及優化則是在逐步接近這個上限。
特徵工程,顧名思義,是對原始資料進行一系列的工程處理,將其提煉為特徵,作為輸入供演算法和模型使用。
本文主要討論以下兩種常用的資料型別。
(1)結構化資料。結構化資料型別可以看做關係型資料庫的一張表,每列都有清晰的定義,包含了數值型和類別型兩種基本型別;每一行資料表示一個樣本的型別。
(2)非結構化資料。非結構化資料主要包括文字、影象、音訊、視訊等資料,其中包含的資訊無法用一個簡單的數值表示,也沒有清晰的類別定義,並且每條資料的大小各不相同。
01 特徵歸一化
為了消除資料特徵之間的量綱影響,我們需要對特徵進行歸一化處理(normalization),使得不同的指標之間具有可比性。
Q1為什麼要對數值型別的特徵做歸一化?
對數值型別的特徵做歸一化可以將所有的特徵都統一到一個大致相同的數值區間內。最常用的方法主要有以下兩種:
-
線性函式歸一化(Min-Max Scaling)。
它對原始資料進行線性變換,使結果對映到[0,1]的範圍,實現對原始資料的等比縮放。歸一化公式如下:
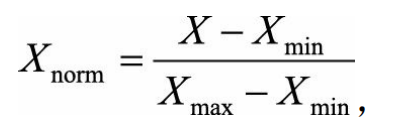
其中X為原始資料,X_max、X_min分別為資料最大值和最小值。 -
零均值歸一化(Z-Score Normalization)
它會將原始資料對映到均值為0、標準差為1的分佈上。具體來說,假設原始特徵的均值為μ、標準差為σ,那麼歸一化公式定義為:
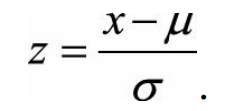
為什麼需要對數值型特徵做歸一化呢? 我們不妨藉助隨機梯度下降的例項來說明歸一化的重要性。假設有兩種數值型特徵,x_1的取值範圍為 [0, 10],x_2的取值範圍為[0, 3],於是可以構造一個目標函式符合圖1.1(a)中的等值圖。
在學習速率相同的情況下,x_1的更新速度會大於x_2,需要較多的迭代才能找到最優解。如果將x_1和x_2歸一化到相同的數值區間後,優化目標的等值圖會變成圖1.1(b)中的圓形,x_1和x_2的更新速度變得更為一致,容易更快地通過梯度下降找到最優解。

資料歸一化並不是萬能的。 在實際應用中,通過梯度下降法求解的模型通常是需要歸一化的,包括線性迴歸、邏輯迴歸、支援向量機、神經網路等模型。但對於決策樹模型則並不適用,決策樹在進行節點分裂時主要依據資料集D關於特徵x的資訊增益比,而資訊增益比跟特徵是否經過歸一化是無關的,因為歸一化並不會改變樣本在特徵x上的資訊增益。
