卷積神經網路的引數計算
前言
這篇文章會簡單寫一下卷積神經網路上引數的計算方法,然後計算各個常見神經網路的引數。一個是加強對網路結構的瞭解,另一方面對網路引數的量級有一個大概的認識,也可以當作備忘錄,免得想知道的時候還要再算。
引數計算方法
全連線的引數計算就不說了,比較簡單。
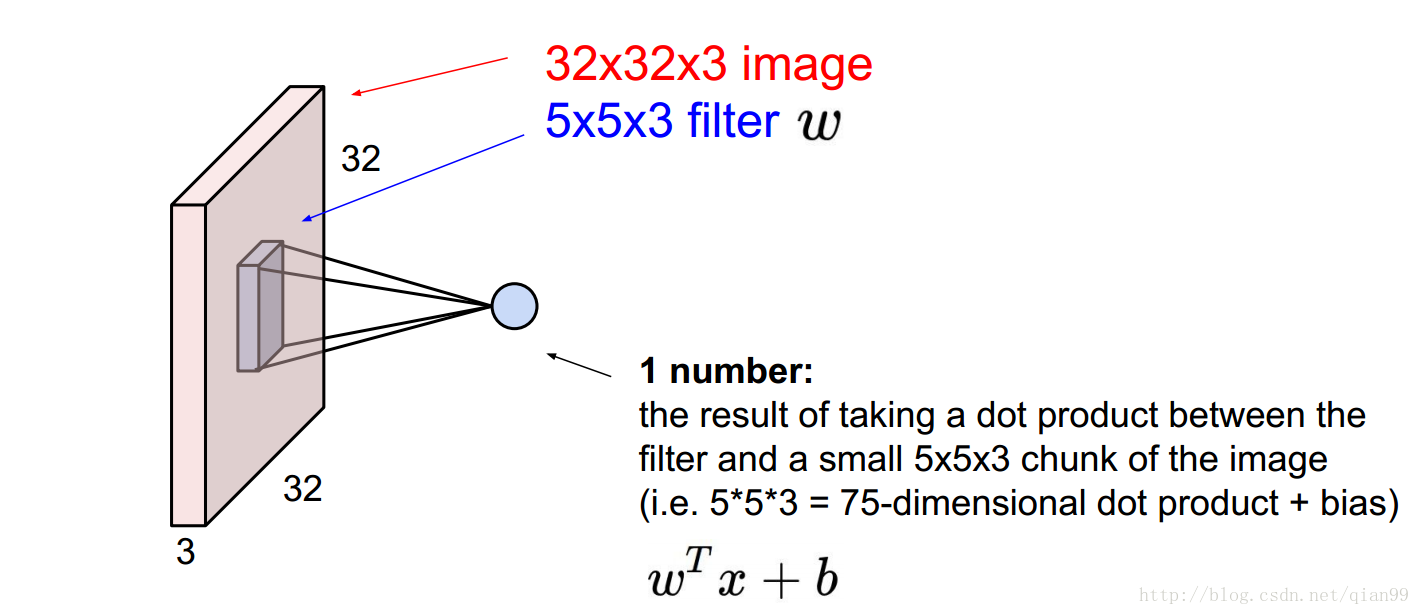
首先,簡單說一下卷積網路的引數計算。下圖中是一個32x32x3的輸入,然後用一個5x5x3的卷積對其中某個位置的計算,這裡算的是一個點積,所以輸出是一個單獨的標量的值。
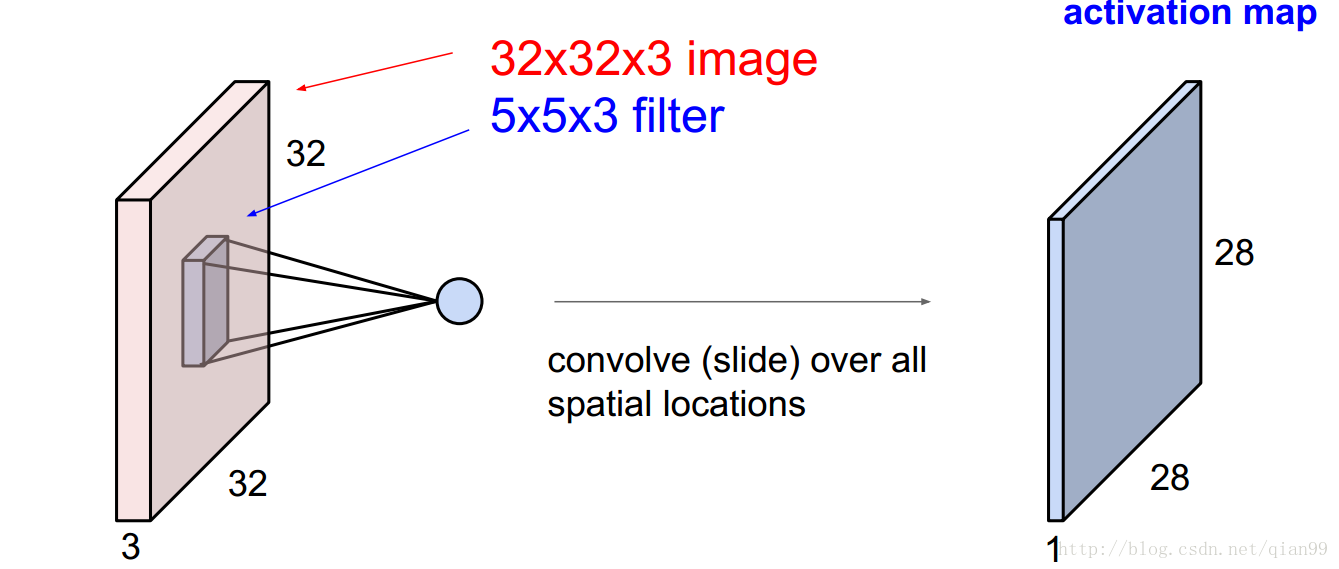
因為卷積的操作是通過一個滑動視窗實現的,那麼通過卷積操作,我們就得到了一個28x28x1的輸出。
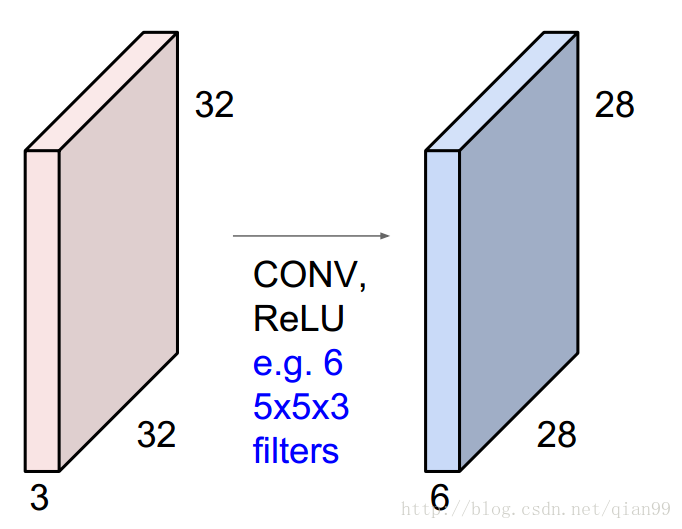
如果我有6個上面說的filter,那麼,我就會得到一個28x28x6的輸出。
這就是一個最基礎的卷積操作,那麼這裡用到的引數是多少呢?我們只需要把每個filter的引數累加起來,當然,不要忘了加上bias:5x5x3x6 + 6 = 456
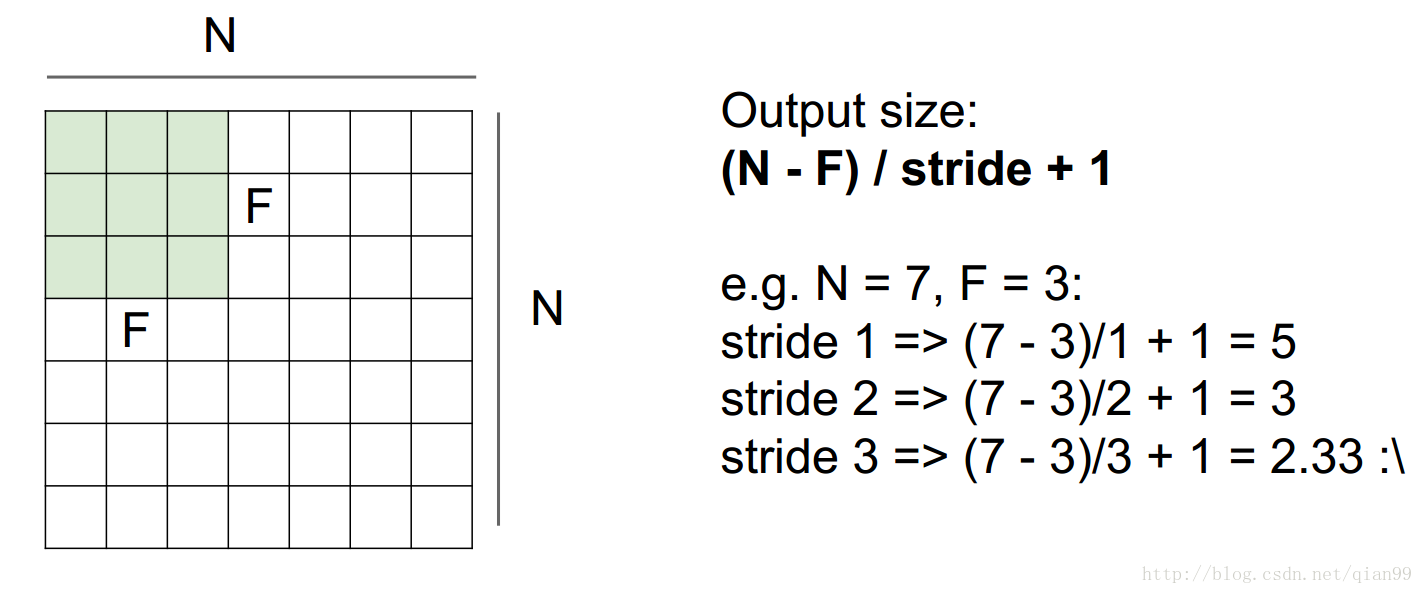
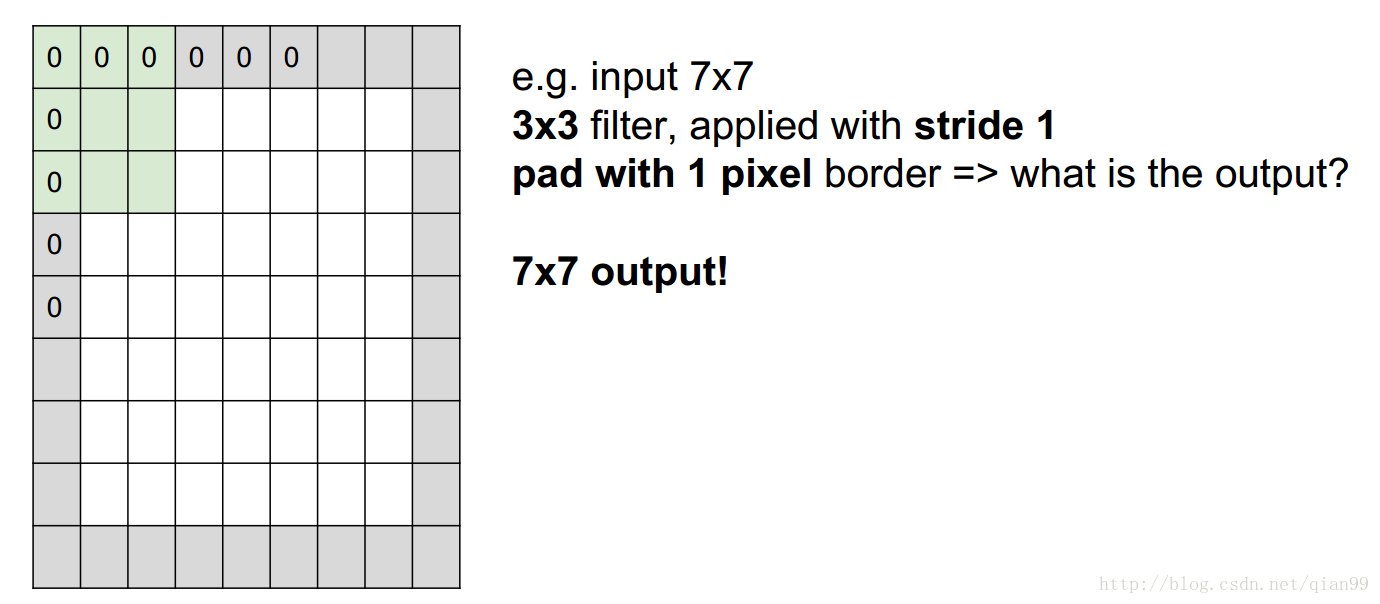
另外一個需要計算的就是進行卷積以後的輸出的大小,從下面的圖上看就很好理解了,用公式直接算就好了。其中N是輸入影象的size,F是filter的size,stride是滑動的步長。
然後從上圖中最後一個例子可以看到,stride大於1的時候不一定能整除,這個時候,就需要在原影象上加上一層padding層,這樣影象的大小就變化了,然後再用前面的公式算就行了。
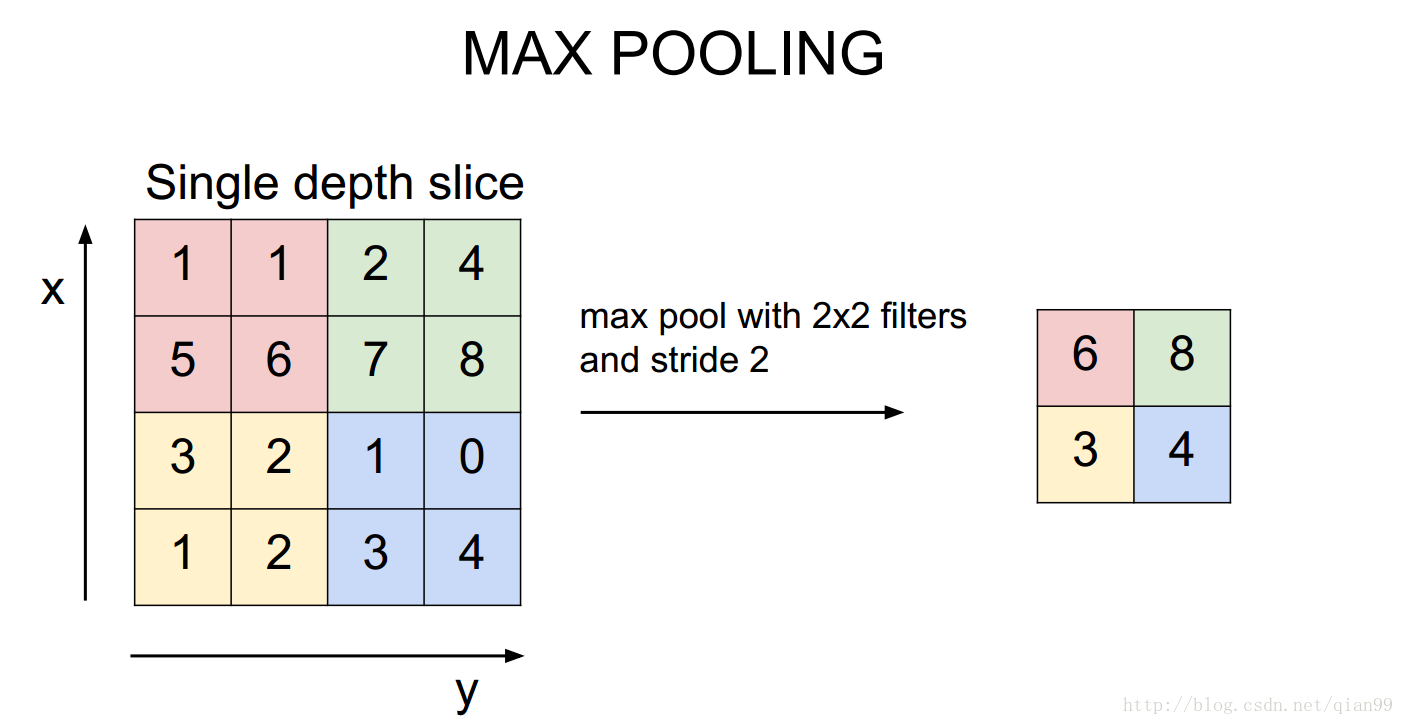
然後還有一個maxpooling操作,這個會改變輸入輸出,但是不會有引數。所以使用和計算卷積一樣的公式算就行了。
LeNet
首先計算一下最簡單的LeNet。網路結構如下:
| 網路層(操作) | 輸入 | filter | stride | padding | 輸出 | 計算公式 | 引數量 |
|---|---|---|---|---|---|---|---|
| Input | 32x32x1 | 32x32x1 | 0 | ||||
| Conv1 | 32x32x1 | 5x5x6 | 1 | 0 | 28x28x6 | 5x5x1x6+6 | 156 |
| MaxPool1 | 28x28x6 | 2x2 | 2 | 0 | 14x14x6 | 0 | |
| Conv2 | 14x14x6 | 5x5x16 | 1 | 0 | 10x10x16 | 5x5x6x16+16 | 2416 |
| MaxPool2 | 10x10x16 | 2x2 | 2 | 0 | 5x5x16 | 0 | |
| FC1 | 5x5x16 | 120 | 5x5x16x120+120 | 48120 | |||
| FC2 | 120 | 84 | 120x84+84 | 10164 | |||
| FC3 | 84 | 10 | 84x10+10 | 850 |
引數總量: 61706
引數記憶體消耗: 241.039KB
AlexNet
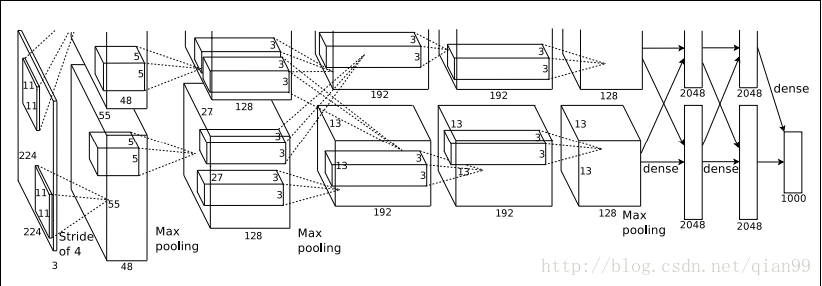
Alexnet的結構圖有些奇怪。但其實是因為要把網路拆分到兩個GPU上,才畫成了兩層,兩層的結構是一樣的,下面計算的時候的結構相當於合併以後的網路。
| 網路層(操作) | 輸入 | filter | stride | padding | 輸出 | 計算公式 | 引數量 |
|---|---|---|---|---|---|---|---|
| Input | 227x227x3 | 227x227x3 | 0 | ||||
| Conv1 | 227x227x3 | 11x11x96 | 4 | 0 | 55x55x96 | 11x11x3x96+96 | 34944 |
| MaxPool1 | 55x55x96 | 3x3 | 2 | 0 | 27x27x96 | 0 | |
| Norm1 | 27x27x96 | 27x27x96 | 0 | ||||
| Conv2 | 27x27x96 | 5x5x256 | 1 | 2 | 27x27x256 | 5x5x96x256+256 | 614656 |
| MaxPool2 | 27x27x256 | 3x3 | 2 | 0 | 13x13x256 | 0 | |
| Norml2 | 13x13x256 | 13x13x256 | 0 | ||||
| Conv3 | 13x13x256 | 3x3x384 | 1 | 1 | 13x13x384 | 3x3x256x384+384 | 885120 |
| Conv4 | 13x13x384 | 3x3x384 | 1 | 1 | 13x13x384 | 3x3x384x384+384 | 1327488 |
| Conv5 | 13x13x384 | 3x3x256 | 1 | 1 | 13x13x256 | 3x3x384x256+256 | 884992 |
| MaxPool3 | 13x13x256 | 3x3 | 2 | 0 | 6x6x256 | 0 | |
| FC6 | 6x6x256 | 4096 | 6x6x256x4096+4096 | 37752832 | |||
| FC7 | 4096 | 4096 | 4096x4096+4096 | 16781312 | |||
| FC8 | 4096 | 1000 | 4096x1000+1000 | 4097000 |
引數總量: 62378344
引數記憶體消耗: 237.9545MB
VGG
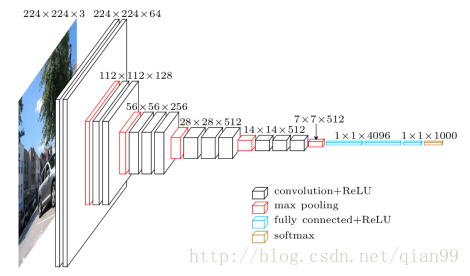
VGG常見有16層和19層的,這裡以16層為例,下面是模型結構圖。
| 網路層(操作) | 輸入 | filter | stride | padding | 輸出 | 計算公式 | 引數量 |
|---|---|---|---|---|---|---|---|
| Input | 224x224x3 | 224x224x3 | 0 | ||||
| Conv3-64 | 224x224x3 | 3x3x64 | 1 | 1 | 224x224x64 | 3x3x3x64 + 64 | 1792 |
| Conv3-64 | 224x224x64 | 3x3x64 | 1 | 1 | 224x224x64 | 3x3x64x64 + 64 | 36928 |
| MaxPool2 | 224x224x64 | 2x2 | 2 | 0 | 112x112x64 | 0 | |
| Conv3-128 | 112x112x64 | 3x3x128 | 1 | 1 | 112x112x128 | 3x3x64x128 + 128 | 73856 |
| Conv3-128 | 112x112x128 | 3x3x128 | 1 | 1 | 112x112x128 | 3x3x128x128 + 128 | 147584 |
| MaxPool2 | 112x112x128 | 2x2 | 2 | 0 | 56x56x128 | 0 | |
| Conv3-256 | 56x56x128 | 3x3x256 | 1 | 1 | 56x56x256 | 3x3x128x256 + 256 | 295168 |
| Conv3-256 | 56x56x256 | 3x3x256 | 1 | 1 | 56x56x256 | 3x3x256x256 + 256 | 590080 |
| Conv3-256 | 56x56x256 | 3x3x256 | 1 | 1 | 56x56x256 | 3x3x256x256 + 256 | 590080 |
| MaxPool2 | 56x56x256 | 2x2 | 2 | 0 | 28x28x256 | 0 | |
| Conv3-512 | 28x28x256 | 3x3x512 | 1 | 1 | 28x28x512 | 3x3x256x512 + 512 | 1180160 |
| Conv3-512 | 28x28x512 | 3x3x512 | 1 | 1 | 28x28x512 | 3x3x512x512 + 512 | 2359808 |
| Conv3-512 | 28x28x512 | 3x3x512 | 1 | 1 | 28x28x512 | 3x3x512x512 + 512 | 2359808 |
| MaxPool2 | 28x28x512 | 2x2 | 2 | 0 | 14x14x512 | 0 | |
| Conv3-512 | 14x14x512 | 3x3x512 | 1 | 1 | 14x14x512 | 3x3x512x512 + 512 | 2359808 |
| Conv3-512 | 14x14x512 | 3x3x512 | 1 | 1 | 14x14x512 | 3x3x512x512 + 512 | 2359808 |
| Conv3-512 | 14x14x512 | 3x3x512 | 1 | 1 | 14x14x512 | 3x3x512x512 + 512 | 2359808 |
| MaxPool2 | 14x14x512 | 2x2 | 2 | 0 | 7x7x512 | 0 | |
| FC1 | 7x7x512 | 4096 | 7x7x512x4096 + 4096 | 102764544 | |||
| FC2 | 4096 | 4096 | 4096*4096 + 4096 | 16781312 | |||
| FC3 | 4096 | 1000 | 4096*1000 + 1000 | 4097000 |
引數總量: 138357544
引數記憶體消耗: 527.7921MB
GoogleNet
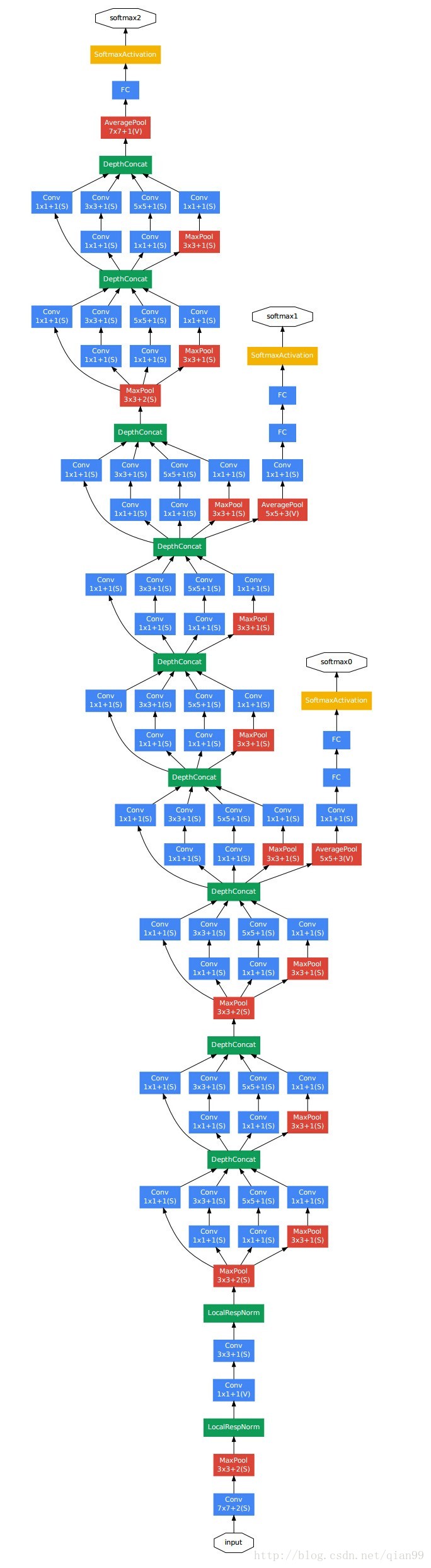
googlenet 提出了inception的概念,用於增加網路深度和寬度,提高深度神經網路效能。下面是googlenet的網路結構:
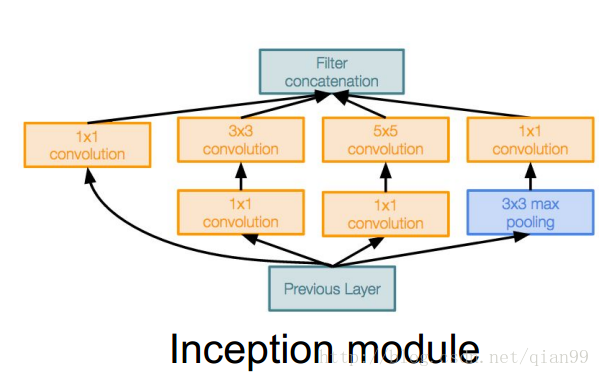
inception的結構如下:
可以看出,inception的結構是多個卷積堆疊,組合而成的。
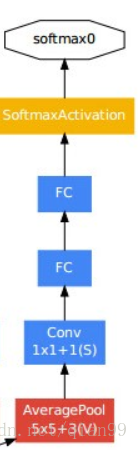
還有,從上面的網路結構中,可以看到一共有三個輸出的分類層:
這個是為了解決深層網路訓練的時候梯度消失的問題,所以在中間加入了幾個全連線層輔助訓練。
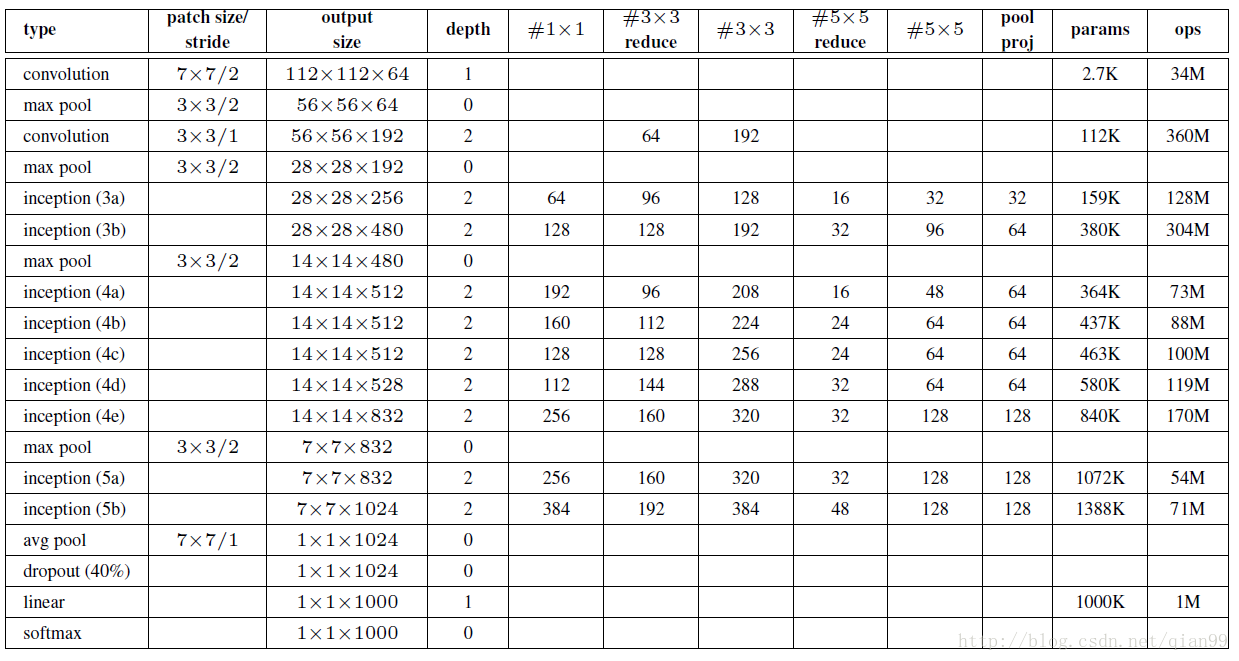
最後,貼一個論文上給出的模型的結構圖:
在這個圖上,已經給出了引數的數量和使用的記憶體,不過我還是說一下inception模組的計算方法和一些注意事項。
- 首先是輸入,輸入的size應該為224x224x3
- 注意第一層的卷積,沒有註明padding,直接算的話,結果是不對的,這裡的padding計算方法和tensorflow中卷積方法padding引數設定為’SAME’是一樣的。簡單來說,就是ceil(size/kernel_size),這個對於下面的計算也是一樣的,總之,就是要填適當的0,使得輸出結果和上圖相對應就是了。
3.在上圖中5~10列對應inception module中的各個卷積操作,對應的值是輸出的feature的數量,對於maxpool操作,他的padding為2,stride為1。
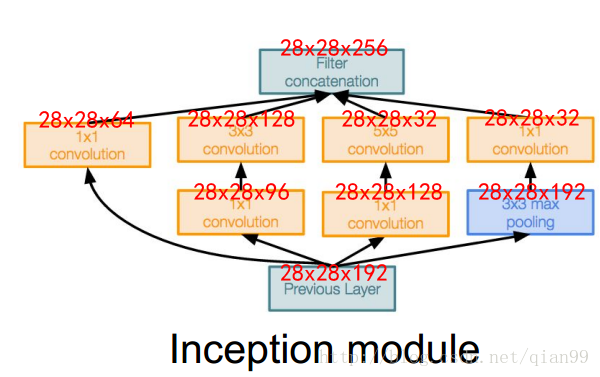
4.當一個inception模組計算完後,它的輸出為各個卷積操作輸出的結果連線起來,也就是如果輸出分別為28x28x64、28x28x128、28x28x32、28x28x32,那麼最終輸出就是28x28x(63+128+32+32)。
下面的圖給出了inception module內部計算的輸出結果。
可以看出googlenet的引數量要比vgg少很多,但是效果確更優秀。
Resnet
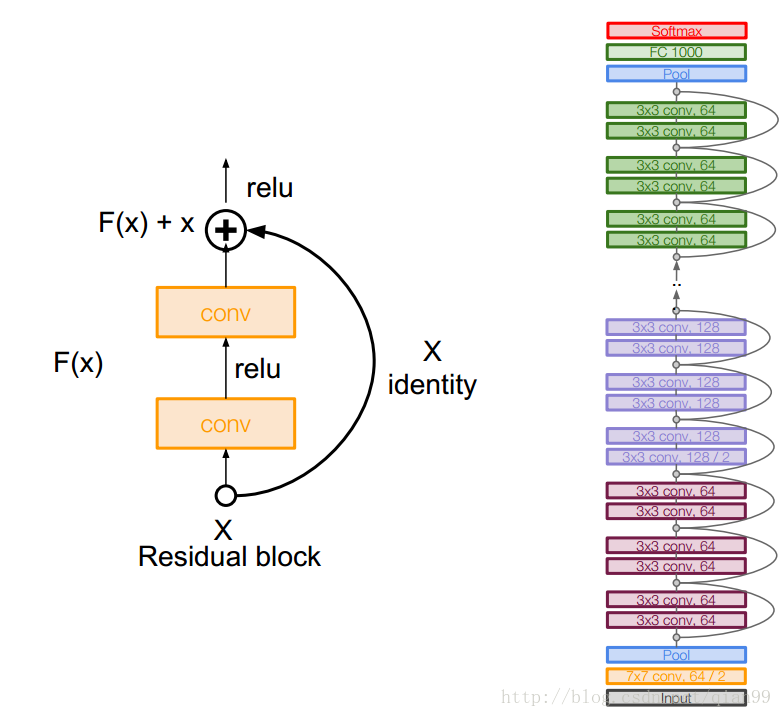
關於resnet,我就不打算計算引數了,因為實在量很大,而且實際上,resnet的基本結構也比較簡單,計算方法和前面的沒什麼差別。這裡就簡單貼一下結構圖好了。
可以看出來,如果沒有中間一條條連線,其實就是一個很深的普通的卷積網路,中間的連線可以保證梯度可以傳遞到低層,防止梯度消失的問題。