在剛剛接觸CNN和caffe之後，也對CNN當中的各類layers做了簡單的瞭解。但對於各個層具體是如何進行運算的，其實並不是特別瞭解。最近調完實驗後，下一步就要進行調參和調網路的工作，所以就準備在這個時間深入地瞭解一下。主要針對conv層、全連線層、pooling層，另外稍帶介紹了CNN中的啟用函式Relu。文章主要參考了零基礎入門深度學習（4）中的內容，並根據本人對於CNN的理解進行了部分修改。

本文將詳細介紹卷積神經網路以及它的訓練演算法，以及動手實現一個簡單的卷積神經網路。

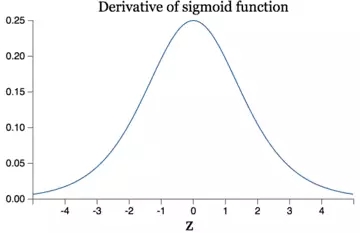
最近幾年卷積神經網路中，啟用函式往往不選擇sigmoid或tanh函式，而是選擇relu函式。Relu函式的定義是：

Relu函式影象如下圖所示：

Relu函式作為啟用函式，有下面幾大優勢：

• 稀疏性 通過對大腦的研究發現，大腦在工作的時候只有大約5%的神經元是啟用的，而採用sigmoid啟用函式的人工神經網路，其啟用率大約是50%。有論文聲稱人工神經網路在15%-30%的啟用率時是比較理想的。因為relu函式在輸入小於0時是完全不啟用的，因此可以獲得一個更低的啟用率。

全連線神經網路之所以不太適合影象識別任務，主要有以下幾個方面的問題：

• 引數數量太多

考慮一個輸入1000*1000畫素的圖片(一百萬畫素，現在已經不能算大圖了)，輸入層有1000*1000=100萬節點。假設第一個隱藏層有100個節點(這個數量並不多)，那麼僅這一層就有(1000*1000+1)*100=1億引數，這實在是太多了！我們看到影象只擴大一點，引數數量就會多很多，因此它的擴充套件性很差。

• 沒有利用畫素之間的位置資訊

對於影象識別任務來說，每個畫素和其周圍畫素的聯絡是比較緊密的，和離得很遠的畫素的聯絡可能就很小了。如果一個神經元和上一層所有神經元相連，那麼就相當於對於一個畫素來說，把影象的所有畫素都等同看待，這不符合前面的假設。當我們完成每個連線權重的學習之後，最終可能會發現，有大量的權重，它們的值都是很小的(也就是這些連線其實無關緊要)。努力學習大量並不重要的權重，這樣的學習必將是非常低效的。

• 網路層數限制

我們知道網路層數越多其表達能力越強，但是通過梯度下降方法訓練深度全連線神經網路很困難，因為全連線神經網路的梯度很難傳遞超過3層。因此，我們不可能得到一個很深的全連線神經網路，也就限制了它的能力。

那麼，卷積神經網路又是怎樣解決這個問題的呢？主要有三個思路：

• 區域性連線：這個是最容易想到的，每個神經元不再和上一層的所有神經元相連，而只和一小部分神經元相連。這樣就減少了很多引數。

• 權值共享：一組連線可以共享同一個權重，而不是每個連線有一個不同的權重，這樣又減少了很多引數。

• 下采樣：可以使用Pooling來減少每層的樣本數，進一步減少引數數量，同時還可以提升模型的魯棒性。

對於影象識別任務來說，卷積神經網路通過儘可能保留重要的引數，去掉大量不重要的引數，來達到更好的學習效果。

接下來，我們將詳述卷積神經網路到底是何方神聖。

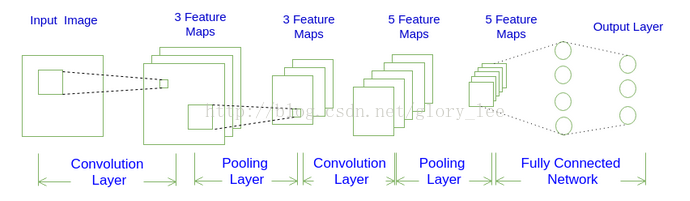
首先，我們先獲取一個感性認識，下圖是一個卷積神經網路的示意圖：

網路架構

如圖1所示，一個卷積神經網路由若干卷積層、Pooling層、全連線層組成。你可以構建各種不同的卷積神經網路，它的常用架構模式為：

INPUT -> [[CONV]*N -> POOL?]*M -> [FC]*K

也就是N個卷積層疊加，然後(可選)疊加一個Pooling層，重複這個結構M次，最後疊加K個全連線層。

對於圖1展示的卷積神經網路：

INPUT -> CONV -> POOL -> CONV -> POOL -> FC -> FC

按照上述模式可以表示為：

INPUT -> [[CONV]*1 -> POOL]*2 -> [FC]*2

也就是：N=1, M=2, K=2。

三維的層結構

從圖1我們可以發現卷積神經網路的層結構和全連線神經網路的層結構有很大不同。全連線神經網路每層的神經元是按照一維排列的，也就是排成一條線的樣子；而卷積神經網路每層的神經元是按照三維排列的，也就是排成一個長方體的樣子，有寬度、高度和深度。

對於圖1展示的神經網路，我們看到輸入層的寬度和高度對應於輸入影象的寬度和高度，而它的深度為1。接著，第一個卷積層對這幅影象進行了卷積操作(後面我們會講如何計算卷積)，得到了三個Feature Map。這裡的"3"可能是讓很多初學者迷惑的地方，實際上，就是這個卷積層包含三個Filter，也就是三套引數，每個Filter都可以把原始輸入影象卷積得到一個Feature Map，三個Filter就可以得到三個Feature Map。至於一個卷積層可以有多少個Filter，那是可以自由設定的。也就是說，卷積層的Filter個數也是一個超引數。我們可以把Feature Map可以看做是通過卷積變換提取到的影象特徵，三個Filter就對原始影象提取出三組不同的特徵，也就是得到了三個Feature Map，也稱做三個通道(channel)。

繼續觀察圖1，在第一個卷積層之後，Pooling層對三個Feature Map做了下采樣(後面我們會講如何計算下采樣)，得到了三個更小的Feature Map。接著，是第二個卷積層，它有5個Filter。每個Fitler都把前面下采樣之後的3個Feature Map卷積在一起，得到一個新的Feature Map。這樣，5個Filter就得到了5個Feature Map。接著，是第二個Pooling，繼續對5個Feature Map進行下采樣，得到了5個更小的Feature Map。

圖1所示網路的最後兩層是全連線層。第一個全連線層的每個神經元，和上一層5個Feature Map中的每個神經元相連，第二個全連線層(也就是輸出層)的每個神經元，則和第一個全連線層的每個神經元相連，這樣得到了整個網路的輸出。

至此，我們對卷積神經網路有了最基本的感性認識。接下來，我們將介紹卷積神經網路中各種層的計算和訓練。

卷積層輸出值的計算

我們用一個簡單的例子來講述如何計算卷積，然後，我們抽象出卷積層的一些重要概念和計算方法。

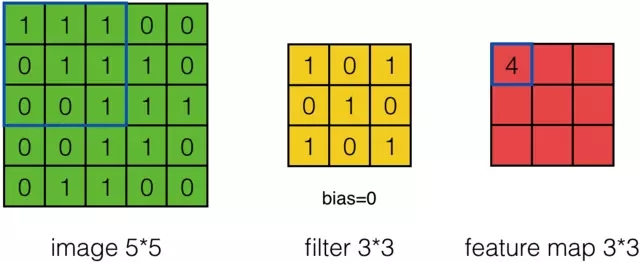
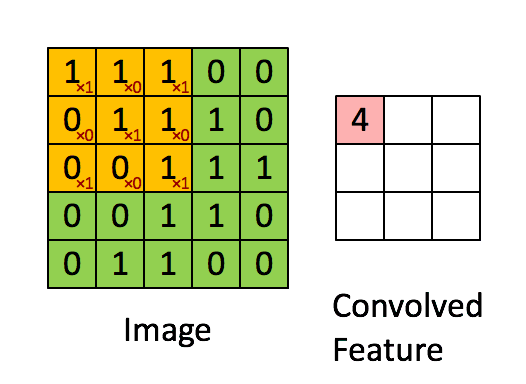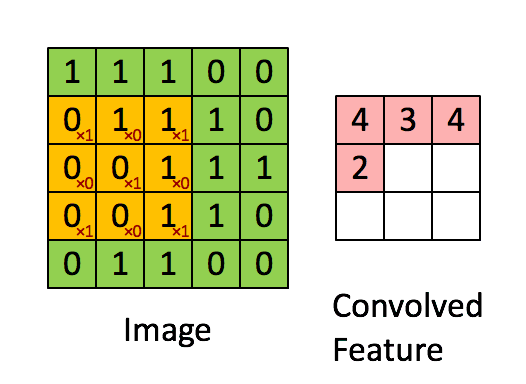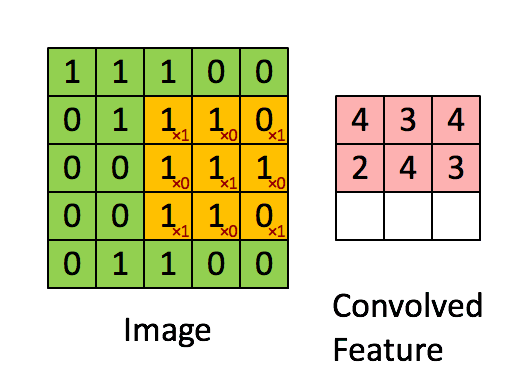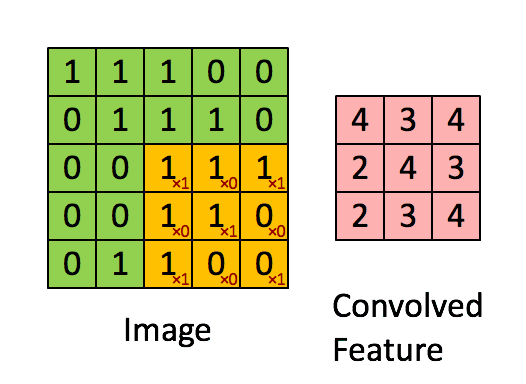
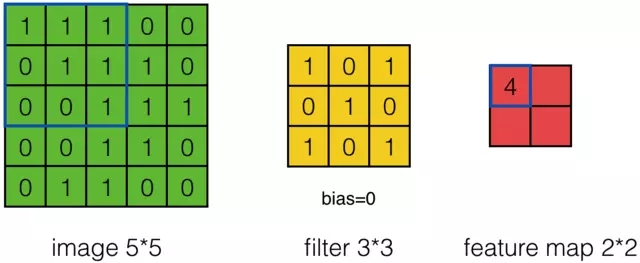
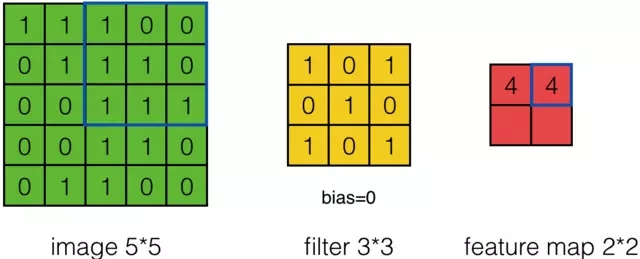
假設有一個5*5的影象，使用一個3*3的filter進行卷積，想得到一個3*3的Feature Map，如下所示：

為了清楚的描述卷積計算過程，我們首先對影象的每個畫素進行編號，用Xi,j表示影象的第行第列元素；對filter的每個權重進行編號，用Wm,n表示第m行第n列權重，用Wb表示filter的偏置項；對Feature Map的每個元素進行編號，用ai,j表示Feature Map的第i行第j列元素；用f表示啟用函式(這個例子選擇relu函式作為啟用函式)。然後，使用下列公式計算卷積：

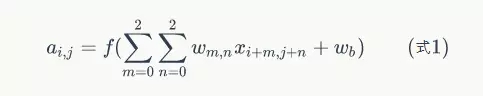
例如，對於Feature Map左上角元素來說，其卷積計算方法為：

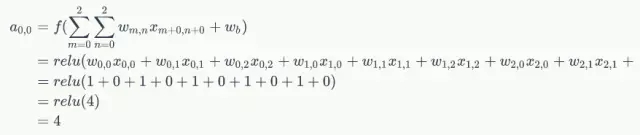
計算結果如下圖所示：

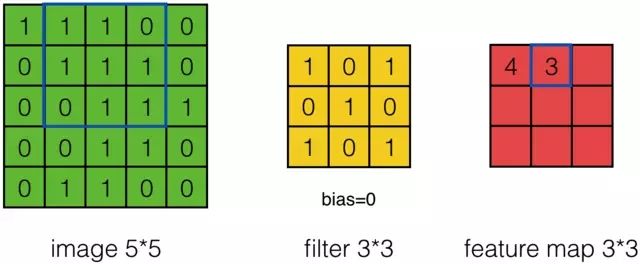
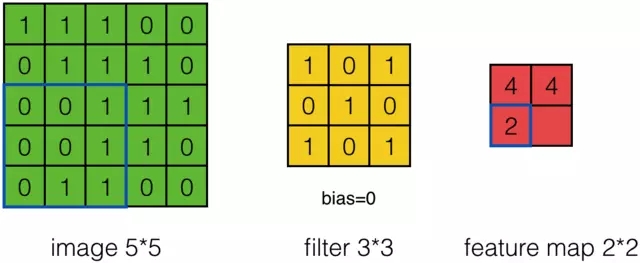
接下來，Feature Map的元素的卷積計算方法為：

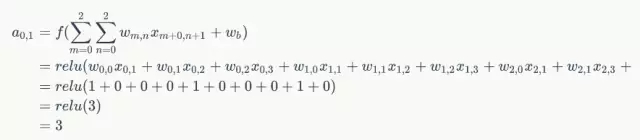
計算結果如下圖所示：

可以依次計算出Feature Map中所有元素的值。下面的動畫顯示了整個Feature Map的計算過程：

上面的計算過程中，步幅(stride)為1。步幅可以設為大於1的數。例如，當步幅為2時，Feature Map計算如下：

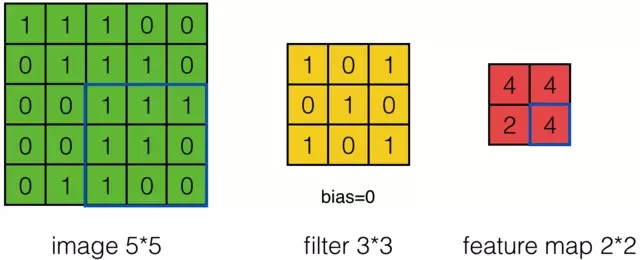
我們注意到，當步幅設定為2的時候，Feature Map就變成2*2了。這說明影象大小、步幅和卷積後的Feature Map大小是有關係的。事實上，它們滿足下面的關係：

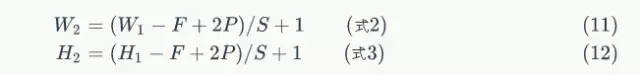
在上面兩個公式中，W2是卷積後Feature Map的寬度；W1是卷積前影象的寬度；F是filter的寬度；P是Zero Padding數量，Zero Padding是指在原始影象周圍補幾圈0，如果P的值是1，那麼就補1圈0；S是步幅；H2是卷積後Feature Map的高度；H1是卷積前影象的寬度。式2和式3本質上是一樣的。

以前面的例子來說，影象寬度W1=5，filter寬度F=3，Zero PaddingP=0，步幅S=2，則

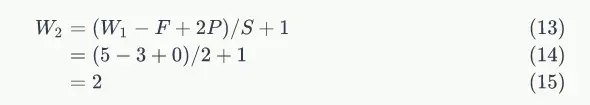
說明Feature Map寬度是2。同樣，我們也可以計算出Feature Map高度也是2。

前面我們已經講了深度為1的卷積層的計算方法，如果深度大於1怎麼計算呢？其實也是類似的。如果卷積前的影象深度為D，那麼相應的filter的深度也必須為D。我們擴充套件一下式1，得到了深度大於1的卷積計算公式：

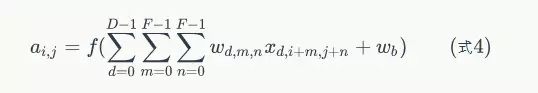
在式4中，D是深度；F是filter的大小(寬度或高度，兩者相同)；Wd,m,n表示filter的第層第m行第n列權重；ad,I,j表示影象的第d層第i行第j列畫素；其它的符號含義和式1是相同的，不再贅述。

我們前面還曾提到，每個卷積層可以有多個filter。每個filter和原始影象進行卷積後，都可以得到一個Feature Map。因此，卷積後Feature Map的深度(個數)和卷積層的filter個數是相同的。

下面的動畫顯示了包含兩個filter的卷積層的計算。我們可以看到7*7*3輸入，經過兩個3*3*3filter的卷積(步幅為2)，得到了3*3*2的輸出。另外我們也會看到下圖的Zero padding是1，也就是在輸入元素的周圍補了一圈0。Zero padding對於影象邊緣部分的特徵提取是很有幫助的。

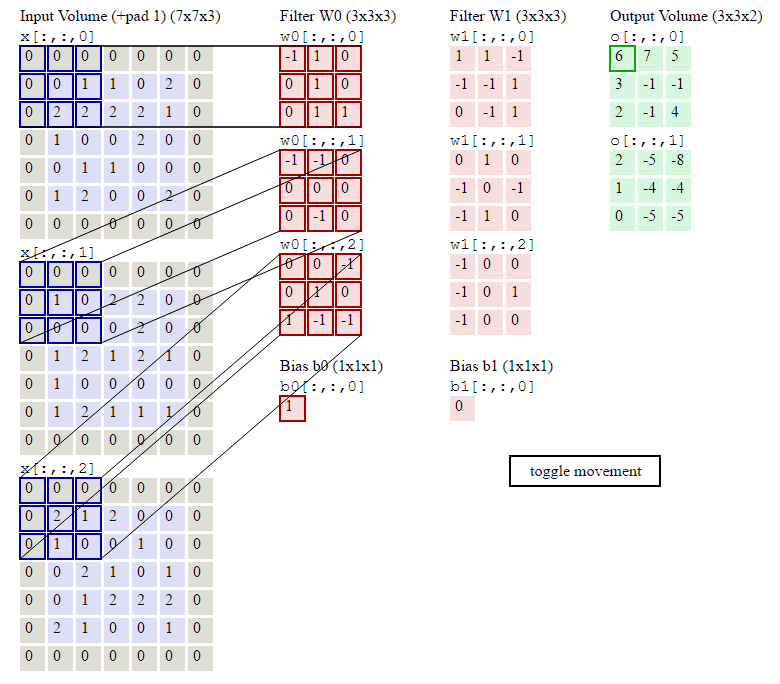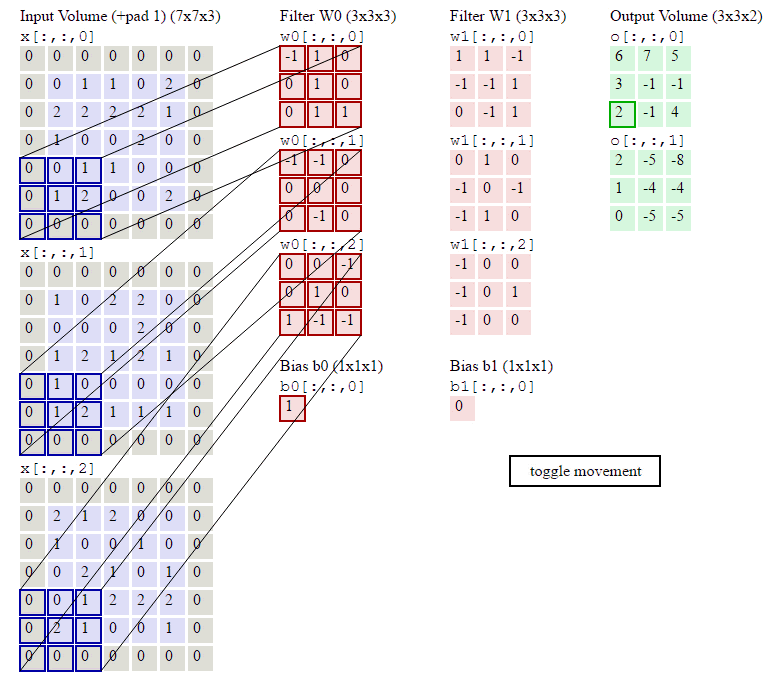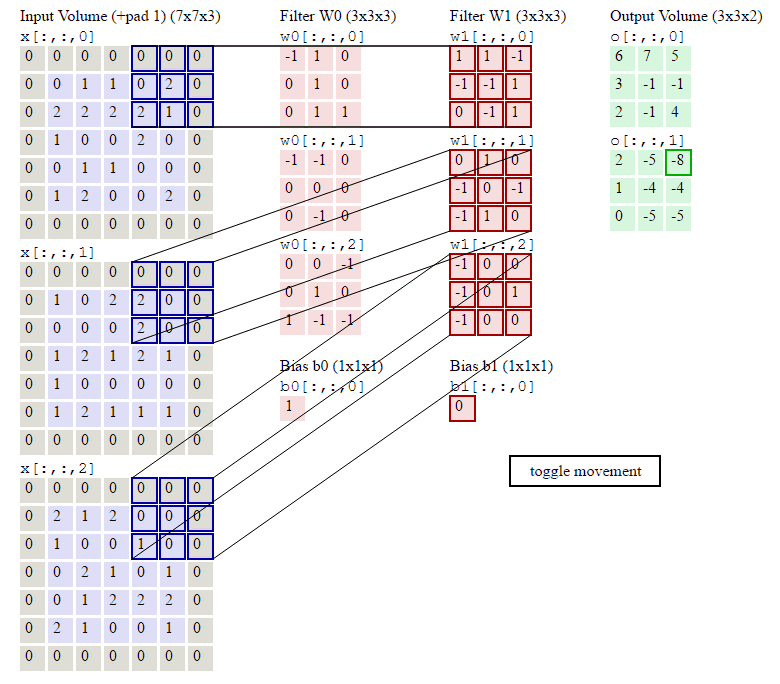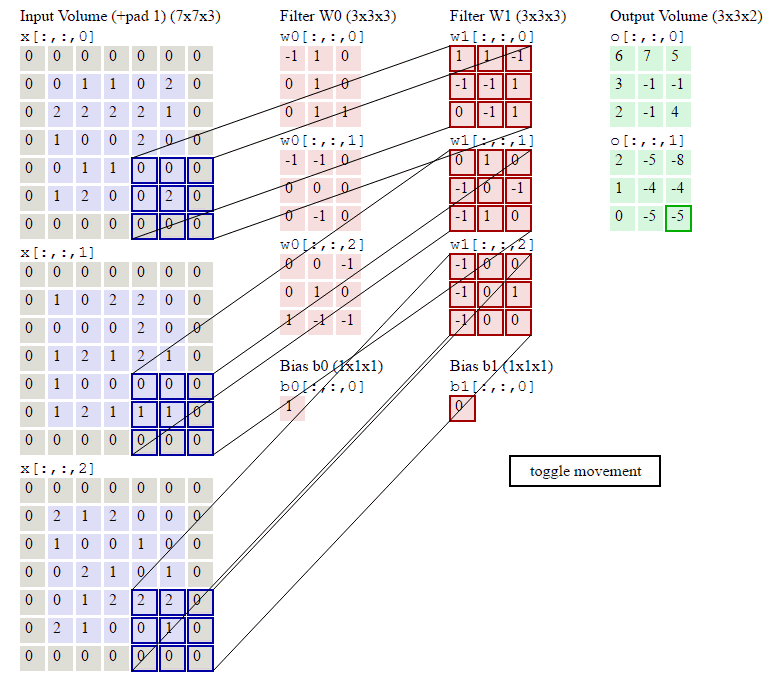
以上就是卷積層的計算方法。這裡面體現了區域性連線和權值共享：每層神經元只和上一層部分神經元相連(卷積計算規則)，且filter的權值對於上一層所有神經元都是一樣的。對於包含兩個3*3*3的fitler的卷積層來說，其引數數量僅有(3*3*3+1)*2=56個，且引數數量與上一層神經元個數無關。與全連線神經網路相比，其引數數量大大減少了。

用卷積公式來表達卷積層計算

不想了解太多數學細節的讀者可以跳過這一節，不影響對全文的理解。

式4的表達很是繁冗，最好能簡化一下。就像利用矩陣可以簡化表達全連線神經網路的計算一樣，我們利用卷積公式可以簡化卷積神經網路的表達。

下面我們介紹二維卷積公式。

設矩陣A，B，其行、列數分別為ma、na、mb、nb，則二維卷積公式如下：

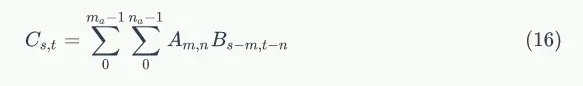
且s,t滿足條件：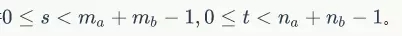

我們可以把上式寫成

如果我們按照式5來計算卷積，我們可以發現矩陣A實際上是filter，而矩陣B是待卷積的輸入，位置關係也有所不同：

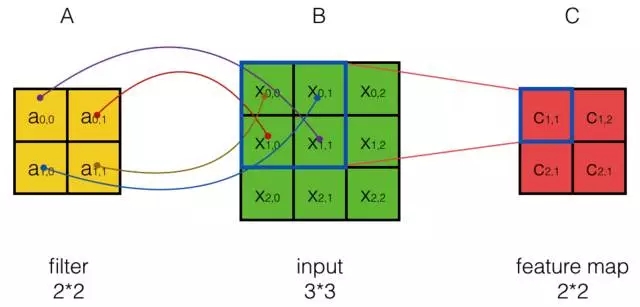
從上圖可以看到，A左上角的值a0,0與B對應區塊中右下角的值b1,1相乘，而不是與左上角的相乘。因此，數學中的卷積和卷積神經網路中的『卷積』還是有區別的，為了避免混淆，我們把卷積神經網路中的『卷積』操作叫做互相關(cross-correlation)操作。

卷積和互相關操作是可以轉化的。首先，我們把矩陣A翻轉180度，然後再交換A和B的位置（即把B放在左邊而把A放在右邊。卷積滿足交換率，這個操作不會導致結果變化），那麼卷積就變成了互相關。

如果我們不去考慮兩者這麼一點點的區別，我們可以把式5代入到式4：

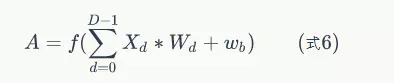
其中，A是卷積層輸出的feature map。同式4相比，式6就簡單多了。然而，這種簡潔寫法只適合步長為1的情況。

Pooling層輸出值的計算

Pooling層主要的作用是下采樣，通過去掉Feature Map中不重要的樣本，進一步減少引數數量。Pooling的方法很多，最常用的是Max Pooling。Max Pooling實際上就是在n*n的樣本中取最大值，作為取樣後的樣本值。下圖是2*2 max pooling：

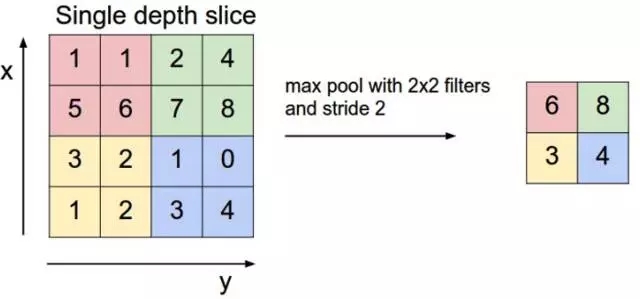
除了Max Pooing之外，常用的還有Mean Pooling——取各樣本的平均值。

對於深度為D的Feature Map，各層獨立做Pooling，因此Pooling後的深度仍然為D。

全連線層

原作者在這裡對於全連線層並沒有進行介紹，只是說參考全連線網路當中的layer。我個人理解全連線層和卷積層比較相似，但全連線層的輸出是一個n*1大小的向量，並通過幾個全連線層對向量進行降維操作，與class進行對應。