1.前言：

影象去噪是訊號處理的一個經典問題，傳統的去噪方法多采用平均或線性法法進行，最常用到的就是維納濾波，但是他的降噪效果並不是很明顯。小波分析法開闢了非線性降噪的先河，小波能夠降噪得益於小波變換的以下特點：低熵性（小波係數稀鬆分佈，使影象變換後的熵降低）、多解析度特性（極好的刻畫了訊號的非平穩性）、去相關性（噪聲在變換後有白化趨勢，小波域更有利於去噪）

目前，主流的小波去噪方法主要集中在三個方面：基於小波變換模極大值降噪、基於相鄰尺度小波係數相關性去燥、基於小波變換域閾值去噪（硬閾值與軟閾值、全域性閾值與區域性自適應閾值）。

2.小波影象去燥實現的步驟：

1.二維訊號的小波分解。選擇一個小波和小波分解的層次N，然後計算訊號s到第N層的分解。

2.對高頻係數進行閾值量化，對於從1~N的每一層，選擇一個閾值，並對這一層的高頻係數進行軟閾值量化處理。

3.二維小波重構

3.小波係數閾值降噪

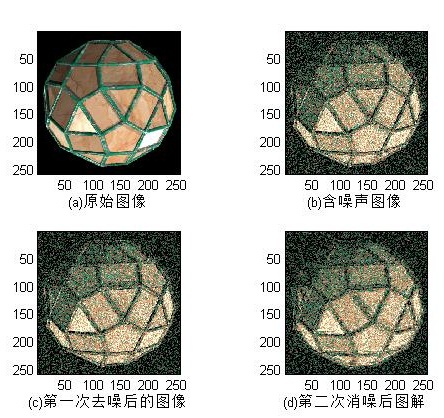
<span style="font-size:18px;">clear all;
load facets;
subplot(221);image(X);
colormap(map);
xlabel('(a)原始影象');
axis square
%產生含噪聲影象
init=2055615866;randn('seed',init)
x=X+50*randn(size(X));
subplot(222);image(x);
colormap(map);
xlabel('(b)含噪聲影象');
axis square
%下面進行影象的去噪處理
%用小波畫數coif3對x進行2層小波分解
[c,s]=wavedec2(x,2,'coif3');
%提取小波分解中第一層的低頻影象，即實現了低通濾波去噪
%設定尺度向量n
n=[1,2];
%設定閾值向量p
p=[10.12,23.28];
%對三個方向高頻係數進行閾值處理
nc=wthcoef2('h',c,s,n,p,'s');
nc=wthcoef2('v',c,s,n,p,'s');
nc=wthcoef2('d',c,s,n,p,'s');
%對新的小波分解結構[nc，s]進行重構
x1=waverec2(nc,s,'coif3');
subplot(223);image(x1);
colormap(map);
xlabel('(c)第一次去噪後的影象');
axis square;
xx=wthcoef2('v',nc,s,n,p,'s');
x2=waverec2(xx,s,'coif2');%影象的二維小波重構
subplot(2,2,4);image(x2);
colormap(map);
xlabel('(d)第二次消噪後圖解');
axis square;
</span>
 

降噪結果：

4.全域性軟閾值降噪

<span style="font-size:18px;"><span style="font-size:18px;">clear all;
load detfingr;
subplot(131);image(X);
colormap(map);
xlabel('(a)原始影象');
axis square;
init=255615866;
randn('state',init);  %新增隨機值
x=X+20*randn(size(X));
subplot(132);image(x);
colormap(map);
xlabel('(b)含噪影象');
axis square;
[thr,sorh,kep]=ddencmp('den','wv',x);   %使用全域性閾值選項進行影象消噪處理
xd=wdencmp('gbl',x,'sym5',2,thr,sorh,kep);
subplot(133);image(xd)
colormap(map);
xlabel('(c)消噪影象');
axis square;</span><span style="font-size:24px;">
</span></span>
 

降噪結果：