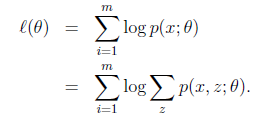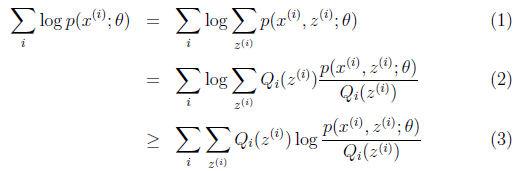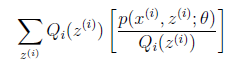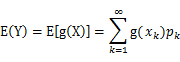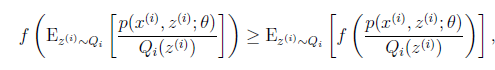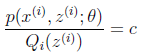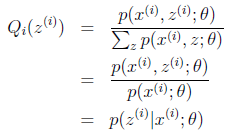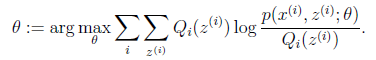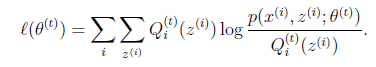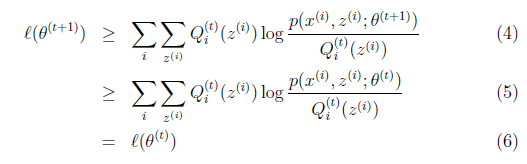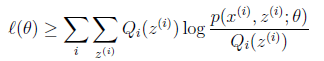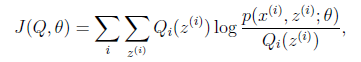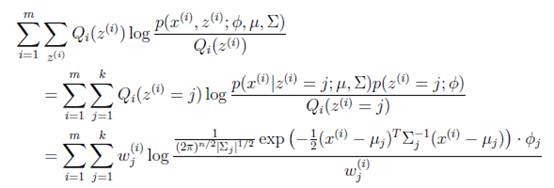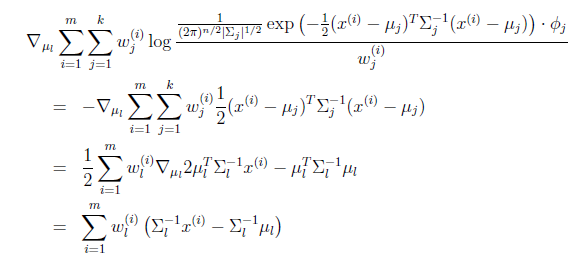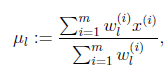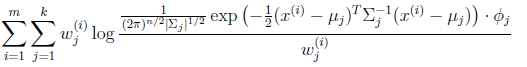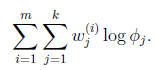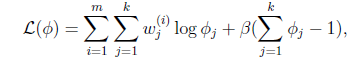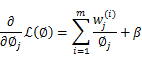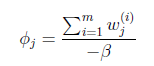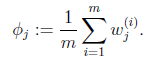EM演算法過程推導
EM是我一直想深入學習的演算法之一,第一次聽說是在NLP課中的HMM那一節,為了解決HMM的引數估計問題,使用了EM演算法。在之後的MT中的詞對齊中也用到了。在Mitchell的書中也提到EM可以用於貝葉斯網路中。
下面主要介紹EM的整個推導過程。
1. Jensen不等式
回顧優化理論中的一些概念。設f是定義域為實數的函式,如果對於所有的實數x,![]() ,那麼f是凸函式。當x是向量時,如果其hessian矩陣H是半正定的(
,那麼f是凸函式。當x是向量時,如果其hessian矩陣H是半正定的(![]() ),那麼f是凸函式。如果
),那麼f是凸函式。如果![]() 或者
或者![]() ,那麼稱f是嚴格凸函式。
,那麼稱f是嚴格凸函式。
Jensen不等式表述如下:
如果f是凸函式,X是隨機變數,那麼
特別地,如果f是嚴格凸函式,那麼![]() 當且僅當
當且僅當![]() ,也就是說X是常量。
,也就是說X是常量。
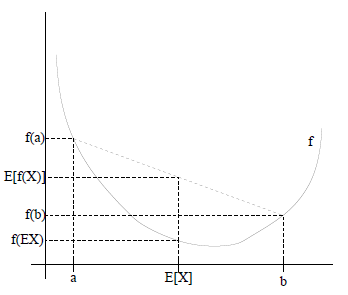
如果用圖表示會很清晰:
圖中,實線f是凸函式,X是隨機變數,有0.5的概率是a,有0.5的概率是b。(就像擲硬幣一樣)。X的期望值就是a和b的中值了,圖中可以看到![]() 成立。
成立。
當f是(嚴格)凹函式當且僅當-f是(嚴格)凸函式。
2. EM演算法
給定的訓練樣本是![]() ,樣例間獨立,我們想找到每個樣例隱含的類別z,能使得p(x,z)最大。p(x,z)的最大似然估計如下:
,樣例間獨立,我們想找到每個樣例隱含的類別z,能使得p(x,z)最大。p(x,z)的最大似然估計如下:
第一步是對極大似然取對數,第二步是對每個樣例的每個可能類別z求聯合分佈概率和。但是直接求![]() 一般比較困難,因為有隱藏變數z存在,但是一般確定了z後,求解就容易了。
一般比較困難,因為有隱藏變數z存在,但是一般確定了z後,求解就容易了。
EM是一種解決存在隱含變數優化問題的有效方法。竟然不能直接最大化![]() ,我們可以不斷地建立
,我們可以不斷地建立![]() 的下界(E步),然後優化下界(M步)。這句話比較抽象,看下面的。
的下界(E步),然後優化下界(M步)。這句話比較抽象,看下面的。
對於每一個樣例i,讓![]() 表示該樣例隱含變數z的某種分佈,
表示該樣例隱含變數z的某種分佈,![]() 滿足的條件是
滿足的條件是![]() 。(如果z是連續性的,那麼
。(如果z是連續性的,那麼![]() 是概率密度函式,需要將求和符號換做積分符號)。比如要將班上學生聚類,假設隱藏變數z是身高,那麼就是連續的高斯分佈。如果按照隱藏變數是男女,那麼就是伯努利分佈了。
是概率密度函式,需要將求和符號換做積分符號)。比如要將班上學生聚類,假設隱藏變數z是身高,那麼就是連續的高斯分佈。如果按照隱藏變數是男女,那麼就是伯努利分佈了。
可以由前面闡述的內容得到下面的公式:
(1)到(2)比較直接,就是分子分母同乘以一個相等的函式。(2)到(3)利用了Jensen不等式,考慮到![]() 是凹函式(二階導數小於0),而且
是凹函式(二階導數小於0),而且
就是![]() 的期望(回想期望公式中的Lazy
Statistician規則)
的期望(回想期望公式中的Lazy
Statistician規則)
|
(1) X是離散型隨機變數,它的分佈律為 |
對應於上述問題,Y是![]() ,X是
,X是![]() ,
,![]() 是
是![]() ,g是
,g是![]() 到
到![]() 的對映。這樣解釋了式子(2)中的期望,再根據凹函式時的Jensen不等式:
的對映。這樣解釋了式子(2)中的期望,再根據凹函式時的Jensen不等式:
可以得到(3)。
這個過程可以看作是對![]() 求了下界。對於
求了下界。對於![]() 的選擇,有多種可能,那種更好的?假設
的選擇,有多種可能,那種更好的?假設![]() 已經給定,那麼
已經給定,那麼![]() 的值就決定於
的值就決定於![]() 和
和![]() 了。我們可以通過調整這兩個概率使下界不斷上升,以逼近
了。我們可以通過調整這兩個概率使下界不斷上升,以逼近![]() 的真實值,那麼什麼時候算是調整好了呢?當不等式變成等式時,說明我們調整後的概率能夠等價於
的真實值,那麼什麼時候算是調整好了呢?當不等式變成等式時,說明我們調整後的概率能夠等價於![]() 了。按照這個思路,我們要找到等式成立的條件。根據Jensen不等式,要想讓等式成立,需要讓隨機變數變成常數值,這裡得到:
了。按照這個思路,我們要找到等式成立的條件。根據Jensen不等式,要想讓等式成立,需要讓隨機變數變成常數值,這裡得到:
c為常數,不依賴於![]() 。對此式子做進一步推導,我們知道
。對此式子做進一步推導,我們知道![]() ,那麼也就有
,那麼也就有![]() ,(多個等式分子分母相加不變,這個認為每個樣例的兩個概率比值都是c),那麼有下式:
,(多個等式分子分母相加不變,這個認為每個樣例的兩個概率比值都是c),那麼有下式:
至此,我們推出了在固定其他引數![]() 後,
後,![]() 的計算公式就是後驗概率,解決了
的計算公式就是後驗概率,解決了![]() 如何選擇的問題。這一步就是E步,建立
如何選擇的問題。這一步就是E步,建立![]() 的下界。接下來的M步,就是在給定
的下界。接下來的M步,就是在給定![]() 後,調整
後,調整![]() ,去極大化
,去極大化![]() 的下界(在固定
的下界(在固定![]() 後,下界還可以調整的更大)。那麼一般的EM演算法的步驟如下:
後,下界還可以調整的更大)。那麼一般的EM演算法的步驟如下:
|
迴圈重複直到收斂 { (E步)對於每一個i,計算 (M步)計算 |
那麼究竟怎麼確保EM收斂?假定![]() 和
和![]() 是EM第t次和t+1次迭代後的結果。如果我們證明了
是EM第t次和t+1次迭代後的結果。如果我們證明了![]() ,也就是說極大似然估計單調增加,那麼最終我們會到達最大似然估計的最大值。下面來證明,選定
,也就是說極大似然估計單調增加,那麼最終我們會到達最大似然估計的最大值。下面來證明,選定![]() 後,我們得到E步
後,我們得到E步
這一步保證了在給定![]() 時,Jensen不等式中的等式成立,也就是
時,Jensen不等式中的等式成立,也就是
然後進行M步,固定![]() ,並將
,並將![]() 視作變數,對上面的
視作變數,對上面的![]() 求導後,得到
求導後,得到![]() ,這樣經過一些推導會有以下式子成立:
,這樣經過一些推導會有以下式子成立:
解釋第(4)步,得到![]() 時,只是最大化
時,只是最大化![]() ,也就是
,也就是![]() 的下界,而沒有使等式成立,等式成立只有是在固定
的下界,而沒有使等式成立,等式成立只有是在固定![]() ,並按E步得到
,並按E步得到![]() 時才能成立。
時才能成立。
第(5)步利用了M步的定義,M步就是將![]() 調整到
調整到![]() ,使得下界最大化。因此(5)成立,(6)是之前的等式結果。
,使得下界最大化。因此(5)成立,(6)是之前的等式結果。
這樣就證明了![]() 會單調增加。一種收斂方法是
會單調增加。一種收斂方法是![]() 不再變化,還有一種就是變化幅度很小。
不再變化,還有一種就是變化幅度很小。
再次解釋一下(4)、(5)、(6)。首先(4)對所有的引數都滿足,而其等式成立條件只是在固定![]() ,並調整好Q時成立,而第(4)步只是固定Q,調整
,並調整好Q時成立,而第(4)步只是固定Q,調整![]() ,不能保證等式一定成立。(4)到(5)就是M步的定義,(5)到(6)是前面E步所保證等式成立條件。也就是說E步會將下界拉到與
,不能保證等式一定成立。(4)到(5)就是M步的定義,(5)到(6)是前面E步所保證等式成立條件。也就是說E步會將下界拉到與![]() 一個特定值(這裡
一個特定值(這裡![]() )一樣的高度,而此時發現下界仍然可以上升,因此經過M步後,下界又被拉昇,但達不到與
)一樣的高度,而此時發現下界仍然可以上升,因此經過M步後,下界又被拉昇,但達不到與![]() 另外一個特定值一樣的高度,之後E步又將下界拉到與這個特定值一樣的高度,重複下去,直到最大值。
另外一個特定值一樣的高度,之後E步又將下界拉到與這個特定值一樣的高度,重複下去,直到最大值。
如果我們定義
從前面的推導中我們知道![]() ,EM可以看作是J的座標上升法,E步固定
,EM可以看作是J的座標上升法,E步固定![]() ,優化
,優化![]() ,M步固定
,M步固定![]() 優化
優化![]() 。
。
3. 重新審視混合高斯模型
我們已經知道了EM的精髓和推導過程,再次審視一下混合高斯模型。之前提到的混合高斯模型的引數![]() 和
和![]() 計算公式都是根據很多假定得出的,有些沒有說明來由。為了簡單,這裡在M步只給出
計算公式都是根據很多假定得出的,有些沒有說明來由。為了簡單,這裡在M步只給出![]() 和
和![]() 的推導方法。
的推導方法。
E步很簡單,按照一般EM公式得到:
簡單解釋就是每個樣例i的隱含類別![]() 為j的概率可以通過後驗概率計算得到。
為j的概率可以通過後驗概率計算得到。
等於0時,得到
在![]() 和
和![]() 確定後,分子上面的一串都是常數了,實際上需要優化的公式是:
確定後,分子上面的一串都是常數了,實際上需要優化的公式是:
這個優化問題我們很熟悉了,直接構造拉格朗日乘子。
求導得,
等於0,得到
![]() 的推導也類似,不過稍微複雜一些,畢竟是矩陣。結果在之前的混合高斯模型中已經給出。
的推導也類似,不過稍微複雜一些,畢竟是矩陣。結果在之前的混合高斯模型中已經給出。
4. 總結
如果將樣本看作觀察值,潛在類別看作是隱藏變數,那麼聚類問題也就是引數估計問題,只不過聚類問題中引數分為隱含類別變數和其他引數,這猶如在x-y座標系中找一個曲線的極值,然而曲線函式不能直接求導,因此什麼梯度下降方法就不適用了。但固定一個變數後,另外一個可以通過求導得到,因此可以使用座標上升法,一次固定一個變數,對另外的求極值,最後逐步逼近極值。對應到EM上,E步估計隱含變數,M步估計其他引數,交替將極值推向最大。EM中還有“硬”指定和“軟”指定的概念,“軟”指定看似更為合理,但計算量要大,“硬”指定在某些場合如K-means中更為實用(要是保持一個樣本點到其他所有中心的概率,就會很麻煩)。
另外,EM的收斂性證明方法確實很牛,能夠利用log的凹函式性質,還能夠想到利用創造下界,拉平函式下界,優化下界的方法來逐步逼近極大值。而且每一步迭代都能保證是單調的。最重要的是證明的數學公式非常精妙,硬是分子分母都乘以z的概率變成期望來套上Jensen不等式,前人都是怎麼想到的。
在Mitchell的Machine Learning書中也舉了一個EM應用的例子,明白地說就是將班上學生的身高都放在一起,要求聚成兩個類。這些身高可以看作是男生身高的高斯分佈和女生身高的高斯分佈組成。因此變成了如何估計每個樣例是男生還是女生,然後在確定男女生情況下,如何估計均值和方差,裡面也給出了公式,有興趣可以參考。