1. Jensen不等式

設 f 是定義域為實數的函式，如果對於所有的實數 x，，那麼 f 是凸函式。當 x 是向量時，如果其hessian矩陣 H 是半正定的（），那麼 f 是凸函式。如果或者，那麼稱 f 是嚴格凸函式。

Jensen不等式表述如下：

如果 f 是凸函式，X是隨機變數，那麼 

特別地，如果 f 是嚴格凸函式，那麼 ，當且僅當，也就是說 x 是常量。這裡我們將簡寫為。

2. 最大似然估計

目標：找出與樣本的分佈最接近的概率分佈模型

概率密度p(x|θ)是高斯分佈N(u,∂)的形式,未知引數是θ=[u, ∂]T。抽到的樣本集是X={x1,x2,…,xN},其中，均值u、方差∂2

最大似然函式是在未知引數是θ的情況下，估計樣本X的類別，用聯合概率形式為：

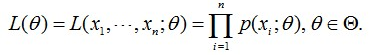
這個概率反映了在概率密度函式的引數是θ時，得到X這組樣本的概率。即：引數θ相對於樣本集

EM演算法推導過程中，會使用到極大似然估計法估計引數，所以，首先給出一個求最大似然函式估計值的一般步驟：

（1）寫出似然函式；

（2）對似然函式取對數，並整理；

（3）求導數，令導數為0，得到似然方程；

（4）解似然方程，得到的引數即為所求；

3. EM演算法

EM演算法是求極大似然借的一種演算法。

給定m個訓練樣本{x(1),…,x(m)x(1),…,x(m)},假設樣本間相互獨立，我們想要擬合模型p(x,z)p(x,z)到資料的引數。根據分佈，我們可以得到如下這個似然函式：

 第一步

EM演算法的核心思想，簡單的歸納一下：

（1）EM演算法通過引入隱含變數,使用MLE（極大似然估計）進行迭代求解引數。

（2）通常引入隱含變數後會有兩個引數，EM演算法首先會固定其中的第一個引數，然後使用MLE計算第二個變數值；

（3）接著通過固定第二個變數，再使用MLE估測第一個變數值；

（3）依次迭代，直至收斂到區域性最優解。

由於演算法保證了每次迭代之後，似然函式都會增加，所以函式最終會收斂。

更加直觀的表示EM演算法迭代過程如下圖：