卡爾曼濾波最通俗易懂的理解
阿新 • • 發佈：2019-01-08
剛剛學過並且試著直觀地理解過，如有不妥的地方還望大牛們指教。
圖片來源及參考文獻：http://www.cl.cam.ac.uk/~rmf25/papers/Understanding%20the%20Basis%20of%20the%20Kalman%20Filter.pdf
題主如果只是想泛泛理解， @Kent Zeng 的回答已經非常棒了。我嘗試做一個更詳細的解答。
好了下面進入正題，先從簡單的說起：
考慮軌道上的一個小車，無外力作用，它在時刻t的狀態向量
只與相關：
（狀態向量就是描述它的t=0時刻所有狀態的向量，比如：
[速度大小5m/s, 速度方向右, 位置座標0]，反正有了這個向量就可以完全預測t=1時刻小車的狀態）
那麼根據t=0時刻的初值，理論上我們可以求出它任意時刻的狀態。
當然，實際情況不會這麼美好。
這個遞推函式可能會受到各種不確定因素的影響
我們假設每個狀態分量受到的不確定因素都服從正態分佈。
現在僅對小車的位置進行估計
請看下圖：t=0時小車的位置服從紅色的正態分佈。
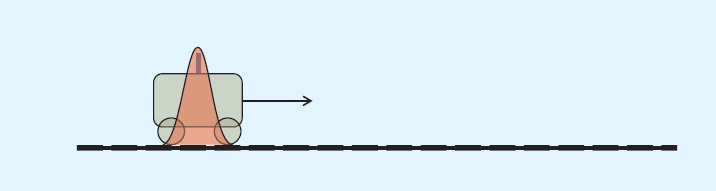
根據小車的這個位置，我們可以預測出t=1時刻它的位置：
分佈變“胖”了，這很好理解——因為在遞推的過程中又加了一層噪聲，所以不確定度變大了。
為了避免純估計帶來的偏差，我們在t=1時刻對小車的位置座標進行一次雷達測量，當然雷達對小車距離的測量也會受到種種因素的影響，於是測量結果告訴我們，小車t=1時的位置服從藍色分佈：
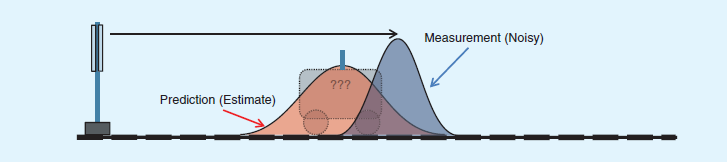
好了，現在我們得到兩個不同的結果。前面有人提過加權，Kalman老先生的牛逼之處就在於找到了相應權值，使紅藍分佈合併為下圖這個綠色的正態分佈
你問為什麼牛逼？
綠色分佈不僅保證了在紅藍給定的條件下，小車位於該點的概率最大，而且，而且，它居然還是一個正態分佈！
正態分佈就意味著，可以把它當做初值繼續往下算了！這是Kalman濾波能夠迭代的關鍵。
最後，把綠色分佈當做第一張圖中的紅色分佈對t=2時刻進行預測，演算法就可以開始迴圈往復了。
你又要問了，說來說去綠色分佈是怎麼得出的呢？
其實可以通過多種方式推匯出來。我們課上講過的就有最大似然法、Ricatti方程法，以及上面參考文獻中提及的直接對高斯密度函式變形的方法，這個不展開說了。
另外，由於我只對小車位移這個一維量做了估計，因此Kalman增益是標量，通常情況下它都是一個矩陣。而且如果估計多維量，還應該引入協方差矩陣的迭代，我也沒有提到。如果樓主有興趣，把我提及那篇參考文獻吃透，就明白了。
Kalman濾波演算法的本質就是利用兩個正態分佈的融合仍是正態分佈這一特性進行迭代而已。
圖片來源及參考文獻：http://www.cl.cam.ac.uk/~rmf25/papers/Understanding%20the%20Basis%20of%20the%20Kalman%20Filter.pdf
題主如果只是想泛泛理解， @Kent Zeng 的回答已經非常棒了。我嘗試做一個更詳細的解答。
好了下面進入正題，先從簡單的說起：
考慮軌道上的一個小車，無外力作用，它在時刻t的狀態向量
（狀態向量就是描述它的t=0時刻所有狀態的向量，比如：
[速度大小5m/s, 速度方向右, 位置座標0]，反正有了這個向量就可以完全預測t=1時刻小車的狀態）
那麼根據t=0時刻的初值
當然，實際情況不會這麼美好。
這個遞推函式可能會受到各種不確定因素的影響
我們假設每個狀態分量受到的不確定因素都服從正態分佈。
現在僅對小車的位置進行估計
請看下圖：t=0時小車的位置服從紅色的正態分佈。
根據小車的這個位置，我們可以預測出t=1時刻它的位置：
分佈變“胖”了，這很好理解——因為在遞推的過程中又加了一層噪聲，所以不確定度變大了。
為了避免純估計帶來的偏差，我們在t=1時刻對小車的位置座標進行一次雷達測量，當然雷達對小車距離的測量也會受到種種因素的影響，於是測量結果告訴我們，小車t=1時的位置服從藍色分佈：
好了，現在我們得到兩個不同的結果。前面有人提過加權，Kalman老先生的牛逼之處就在於找到了相應權值，使紅藍分佈合併為下圖這個綠色的正態分佈
你問為什麼牛逼？綠色分佈不僅保證了在紅藍給定的條件下，小車位於該點的概率最大，而且，而且，它居然還是一個正態分佈！
正態分佈就意味著，可以把它當做初值繼續往下算了！這是Kalman濾波能夠迭代的關鍵。
最後，把綠色分佈當做第一張圖中的紅色分佈對t=2時刻進行預測，演算法就可以開始迴圈往復了。
你又要問了，說來說去綠色分佈是怎麼得出的呢？
其實可以通過多種方式推匯出來。我們課上講過的就有最大似然法、Ricatti方程法，以及上面參考文獻中提及的直接對高斯密度函式變形的方法，這個不展開說了。
另外，由於我只對小車位移這個一維量做了估計，因此Kalman增益是標量，通常情況下它都是一個矩陣。而且如果估計多維量，還應該引入協方差矩陣的迭代，我也沒有提到。如果樓主有興趣，把我提及那篇參考文獻吃透，就明白了。
Kalman濾波演算法的本質就是利用兩個正態分佈的融合仍是正態分佈這一特性進行迭代而已。