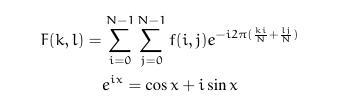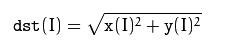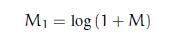2. 程式人生 > >數字影象處理-離散傅立葉變換（opencv3+C++顯示）

數字影象處理-離散傅立葉變換（opencv3+C++顯示）

阿新 • • 發佈：2019-01-09

參考：

http://daily.zhihu.com/story/3935067

http://blog.csdn.net/keith_bb/article/details/53389819

在學習訊號與系統或通訊原理等課程裡面可能對傅立葉變換有了一定的瞭解。我們知道傅立葉變換是把一個訊號從時域變換到其對應的頻域進行分析。如果有小夥伴還對傅立葉變換處於很迷糊的狀態，請戳這裡，非常通俗易懂。而在影象處理中也有傅立葉分析的概念，我這裡給出在其官方指導檔案opencv_tutorials中給出的解釋。 
傅立葉變換可以將一幅圖片分解為正弦和餘弦兩個分量，換而言之，他可以將一幅影象從其空間域（spatial domain）轉換為頻域（frequency domain）。這種變換的思想是任何函式可以很精確的接近無窮個sin()函式和cos()函式的和。傅立葉變換提供了這種方法來達到這種效果。對於二點陣圖像其傅立葉變換公式如下： 
這裡寫圖片描述

 
式中f(i, j)是影象空間域的值而F是頻域的值。傅立葉轉換的結果是複數，這也顯示出了傅立葉變換是一副實數影象（real image）和虛數影象（complex image）疊加或者是幅度影象（magitude image）和相點陣圖像（phase image）疊加的結果。在實際的影象處理演算法中僅有幅度影象（magnitude image）影象能夠用到，因為幅度影象包含了我們所需要的所有影象幾何結構的資訊。但是，如果想通過修改幅度影象或者相點陣圖像來間接修改原空間影象，需要保留幅度影象和相點陣圖像來進行傅立葉逆變換，從而得到修改後影象。

1.dft()

首先看一下opencv提供的傅立葉變換函式dft()，其定義如下：

C++: void dft(InputArray src, OutputArray dst, int flags=0, int nonzeroRows=0);
  • 1

引數解釋： 
. InputArray src: 輸入影象，可以是實數或虛數 
. OutputArray dst: 輸出影象，其大小和型別取決於第三個引數flags 
. int flags = 0: 轉換的識別符號，有預設值0.其可取的值如下所示： 
。DFT_INVERSE: 用一維或二維逆變換取代預設的正向變換 
。DFT_SCALE: 縮放比例識別符號，根據資料元素個數平均求出其縮放結果，如有N個元素，則輸出結果以1/N縮放輸出，常與DFT_INVERSE搭配使用。 
。DFT_ROWS: 對輸入矩陣的每行進行正向或反向的傅立葉變換；此識別符號可在處理多種適量的的時候用於減小資源的開銷，這些處理常常是三維或高維變換等複雜操作。 
。DFT_COMPLEX_OUTPUT: 對一維或二維的實數陣列進行正向變換，這樣的結果雖然是複數陣列，但擁有複數的共軛對稱性（CCS），可以以一個和原陣列尺寸大小相同的實數陣列進行填充，這是最快的選擇也是函式預設的方法。你可能想要得到一個全尺寸的複數陣列（像簡單光譜分析等等），通過設定標誌位可以使函式生成一個全尺寸的複數輸出陣列。 
。DFT_REAL_OUTPUT: 對一維二維複數陣列進行逆向變換，這樣的結果通常是一個尺寸相同的複數矩陣，但是如果輸入矩陣有複數的共軛對稱性（比如是一個帶有DFT_COMPLEX_OUTPUT識別符號的正變換結果），便會輸出實數矩陣。 
. int nonzeroRows = 0: 當這個引數不為0，函式會假設只有輸入陣列（沒有設定DFT_INVERSE）的第一行或第一個輸出陣列（設定了DFT_INVERSE）包含非零值。這樣的話函式就可以對其他的行進行更高效的處理節省一些時間，這項技術尤其是在採用DFT計算矩陣卷積時非常有效。

2. getOptimalDFTSize()

返回給定向量尺寸經過DFT變換後結果的最優尺寸大小。其函式定義如下：

C++: int getOptimalDFTSize(int vecsize);
  • 1

引數解釋： 
int vecsize: 輸入向量尺寸大小(vector size) 
DFT變換在一個向量尺寸上不是一個單調函式，當計算兩個陣列卷積或對一個數組進行光學分析，它常常會用0擴充一些陣列來得到稍微大點的陣列以達到比原來陣列計算更快的目的。一個尺寸是2階指數（2,4,8,16,32…）的陣列計算速度最快，一個數組尺寸是2、3、5的倍數（例如：300 = 5*5*3*2*2）同樣有很高的處理效率。 
getOptimalDFTSize()函式返回大於或等於vecsize的最小數值N，這樣尺寸為N的向量進行DFT變換能得到更高的處理效率。在當前N通過p,q,r等一些整數得出N = 2^p*3^q*5^r. 
這個函式不能直接用於DCT（離散餘弦變換）最優尺寸的估計，可以通過getOptimalDFTSize((vecsize+1)/2)*2得到。

3.magnitude()

計算二維向量的幅值，其定義如下：

C++: void magnitude(InputArray x, InputArray y, OutputArray magnitude)；
  • 1

引數解釋： 
. InputArray x: 浮點型陣列的x座標向量，也就是實部 
. InputArray y: 浮點型陣列的y座標向量，必須和x尺寸相同 
. OutputArray magnitude: 與x型別和尺寸相同的輸出陣列 
其計算公式如下： 
這裡寫圖片描述

4. copyMakeBorder() 
擴充影象邊界，其函式定義如下：

C++: void copyMakeBorder(InputArray src, OutputArray dst, int top, int bottom, int left, int right, int borderType, const Scalar& value=Scalar() )；
  • 1

引數解釋： 
. InputArray src: 輸入影象 
. OutputArray dst: 輸出影象，與src影象有相同的型別，其尺寸應為Size(src.cols+left+right, src.rows+top+bottom) 
. int型別的top、bottom、left、right: 在影象的四個方向上擴充畫素的值 
. int borderType: 邊界型別，由borderInterpolate()來定義，常見的取值為BORDER_CONSTANT 
. const Scalar& value = Scalar(): 如果邊界型別為BORDER_CONSTANT則表示為邊界值

5. normalize() 
歸一化就是把要處理的資料經過某種演算法的處理限制在所需要的範圍內。首先歸一化是為了後面資料處理的方便，其次歸一化能夠保證程式執行時收斂加快。歸一化的具體作用是歸納同意樣本的統計分佈性，歸一化在0-1之間是統計的概率分佈，歸一化在某個區間上是統計的座標分佈，在機器學習演算法的資料預處理階段，歸一化也是非常重要的步驟。其定義如下：

C++: void normalize(InputArray src, OutputArray dst, double alpha=1, double beta=0, int norm_type=NORM_L2, int dtype=-1, InputArray mask=noArray() )
  • 1

引數解釋： 
. InputArray src: 輸入影象 
. OutputArray dst: 輸出影象，尺寸大小和src相同 
. double alpha = 1: range normalization模式的最小值 
. double beta = 0: range normalization模式的最大值，不用於norm normalization(範數歸一化)模式 
. int norm_type = NORM_L2: 歸一化的型別，主要有 
。NORM_INF: 歸一化陣列的C-範數（絕對值的最大值） 
。NORM_L1: 歸一化陣列的L1-範數（絕對值的和） 
。NORM_L2: 歸一化陣列的L2-範數（歐幾里得） 
。NORM_MINMAX: 陣列的數值被平移或縮放到一個指定的範圍，線性歸一化，一般較常用。 
. int dtype = -1: 當該引數為負數時，輸出陣列的型別與輸入陣列的型別相同，否則輸出陣列與輸入陣列只是通道數相同，而depth = CV_MAT_DEPTH(dtype) 
. InputArray mask = noArray(): 操作掩膜版，用於指示函式是否僅僅對指定的元素進行操作。

示例程式：

#include <iostream>
#include <opencv2/core.hpp>
#include <opencv2/highgui.hpp>
#include <opencv2/imgproc.hpp>

using namespace std;
using namespace cv;

int main()
{
    Mat I = imread("lena.jpg", IMREAD_GRAYSCALE);       //讀入影象灰度圖

    //判斷影象是否載入成功
    if (I.empty())
    {
        cout << "影象載入失敗!" << endl;
        return -1;
    }
    else
        cout << "影象載入成功!" << endl << endl;

    Mat padded;                 //以0填充輸入影象矩陣
    int m = getOptimalDFTSize(I.rows);
    int n = getOptimalDFTSize(I.cols);

    //填充輸入影象I，輸入矩陣為padded，上方和左方不做填充處理
    copyMakeBorder(I, padded, 0, m - I.rows, 0, n - I.cols, BORDER_CONSTANT, Scalar::all(0));

    Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(),CV_32F) };
    Mat complexI;
    merge(planes, 2, complexI);     //將planes融合合併成一個多通道陣列complexI

    dft(complexI, complexI);        //進行傅立葉變換

    //計算幅值，轉換到對數尺度(logarithmic scale)
    //=> log(1 + sqrt(Re(DFT(I))^2 + Im(DFT(I))^2))
    split(complexI, planes);        //planes[0] = Re(DFT(I),planes[1] = Im(DFT(I))
                                    //即planes[0]為實部,planes[1]為虛部
    magnitude(planes[0], planes[1], planes[0]);     //planes[0] = magnitude
    Mat magI = planes[0];

    magI += Scalar::all(1);
    log(magI, magI);                //轉換到對數尺度(logarithmic scale)

    //如果有奇數行或列，則對頻譜進行裁剪
    magI = magI(Rect(0, 0, magI.cols&-2, magI.rows&-2));

    //重新排列傅立葉影象中的象限，使得原點位於影象中心
    int cx = magI.cols / 2;
    int cy = magI.rows / 2;

    Mat q0(magI, Rect(0, 0, cx, cy));       //左上角影象劃定ROI區域
    Mat q1(magI, Rect(cx, 0, cx, cy));      //右上角影象
    Mat q2(magI, Rect(0, cy, cx, cy));      //左下角影象
    Mat q3(magI, Rect(cx, cy, cx, cy));     //右下角影象

    //變換左上角和右下角象限
    Mat tmp;
    q0.copyTo(tmp);
    q3.copyTo(q0);
    tmp.copyTo(q3);

    //變換右上角和左下角象限
    q1.copyTo(tmp);
    q2.copyTo(q1);
    tmp.copyTo(q2);

    //歸一化處理，用0-1之間的浮點數將矩陣變換為可視的影象格式
    normalize(magI, magI, 0, 1, CV_MINMAX);

    imshow("輸入影象", I);
    imshow("頻譜圖", magI);
    waitKey(0);


    return 0;
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77

程式分析： 
1.影象填充：

Mat padded;
int m = getOptimalDFTSize(I.rows);
int n = getOptimalDFTSize(I.cols);
copyMakeBorder(I, padded, 0, m - I.rows, 0, n - I.cols, BORDER_CONSTANT, Scalar::all(0));
  • 1
  • 2
  • 3
  • 4

根據前面的理論介紹可以知道當影象尺寸為2、3、5的倍數時可以得到最快的處理速度，所以通過getOptimalDFTSize()函式獲取最佳DFT變換尺寸，之後再結合copyMakeBorder()函式對影象進行擴充。

2.為實部和虛部分配儲存空間

Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(),CV_32F) };
Mat complexI;
merge(planes, 2, complexI);
  • 1
  • 2
  • 3

傅立葉變換的結果是複數，這就意味著經過傅立葉變換每個影象值都會變成兩個值，此外其頻域(frequency domains)範圍比空間域(spatial counterpart)範圍大很多。我們通常以浮點型資料格式對結果進行儲存。因此我們將輸入影象轉換為這種型別，通過另外的通道擴充影象。

3.傅立葉變換

dft(complexI, complexI);
  • 1

傅立葉變換函式，對影象進行傅立葉變換。

4.將實數和複數的值轉換為幅度值

split(complexI, planes);
magnitude(planes[0], planes[1], planes[0]); 
Mat magI = planes[0];
  • 1
  • 2
  • 3

複數包含實部和虛部兩個部分，傅立葉變換的結果是一個複數，傅立葉變換的幅度計算公式是：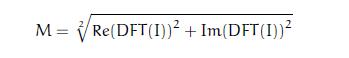 
這裡寫圖片描述 
5.轉換為對數尺度(Switch to a logarithmic scale)

magI += Scalar::all(1);
log(magI, magI);
  • 1
  • 2

之所以要進行對數轉換是因為傅立葉變換後的結果對於在顯示器顯示來講範圍比較大，這樣的話對於一些小的變化或者是高的變換值不能進行觀察。因此高的變化值將會轉變成白點，而較小的變化值則會變成黑點。為了能夠獲得視覺化的效果，可以利用灰度值將我們的線性尺度(linear scale)轉變為對數尺度(logarithmic scale)，其計算公式如下： 
這裡寫圖片描述

6.剪下和象限變換

magI = magI(Rect(0, 0, magI.cols&-2, magI.rows&-2));
int cx = magI.cols / 2;
int cy = magI.rows / 2;

Mat q0(magI, Rect(0, 0, cx, cy));
Mat q1(magI, Rect(cx, 0, cx, cy));  
Mat q2(magI, Rect(0, cy, cx, cy));
Mat q3(magI, Rect(cx, cy, cx, cy)); 

//變換左上角和右下角象限
Mat tmp;
q0.copyTo(tmp);
q3.copyTo(q0);
tmp.copyTo(q3);

//變換右上角和左下角象限
q1.copyTo(tmp);
q2.copyTo(q1);
tmp.copyTo(q2);
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19

在進行傅立葉變換時，為了取得更快的計算效果，對影象進行了擴充，現在就需要對新增加的行列進行裁剪了。為了視覺化的需要，我們同樣需要對顯示的結果影象畫素進行調整，如果不進行調整，最後顯示的結果是這樣的：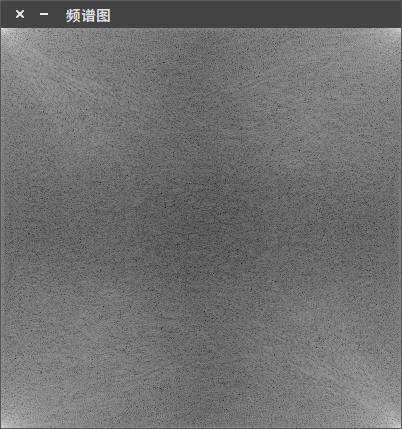 
這裡寫圖片描述 
可以看到四周的角上時高頻分量，現在我們通過重新調整象限將高頻分量調整到影象正中間。

7.歸一化

normalize(magI, magI, 0, 1, CV_MINMAX);
  • 1

對結果進行歸一化處理同樣是處於視覺化的目的。現在我們得到了幅度值，但是這仍然超出了0-1的顯示範圍。這就需要利用normalize()函式對資料進行歸一化處理。

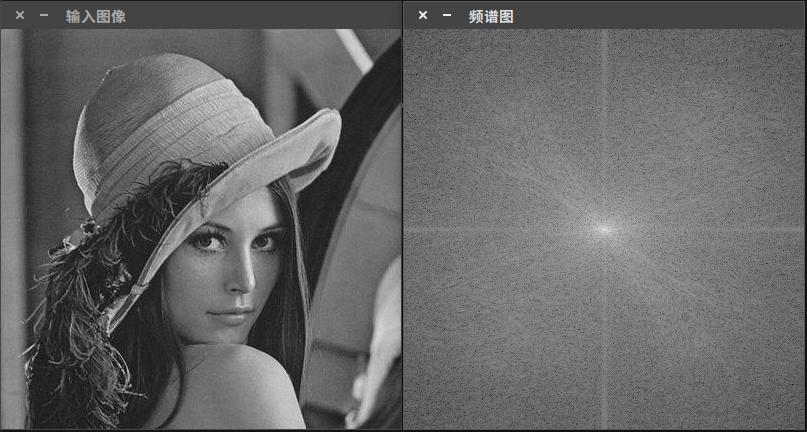
程式執行結果如圖： 
這裡寫圖片描述

相關推薦

數字影象處理-離散傅立葉變換（opencv3+C++顯示）

參考： http://daily.zhihu.com/story/3935067 http://blog.csdn.net/keith_bb/article/details/53389819 在學習訊號與系統或通訊原理等課程裡面可能對傅立葉變換有了一定的瞭解。我們知道傅立葉變換是把一個訊號從時域變換

影象處理-離散傅立葉變換-數字影象處理第三版第四章內容

  影象傅立葉變換方法有很多，可以通過空間光調製器輸入影象後在通過平行光照明經過傅立葉變換透鏡進行傅立葉變換，另一個方法就是利用計算機進行傅立葉變換，其中傅立葉變換有兩種演算法一種是DFT還有一種是FFT(快速傅立葉變換)。   首先我介紹一下影象的定義，影象是怎麼去得到的

數字影象處理筆記——二維離散傅立葉變換（2D Discrete Fourier Transform）

二維傅立葉變換 我們先來看看一維情況的傅立葉變換。在訊號系統中講過連續時間的傅立葉變換和離散時間的傅立葉變換，連續時間傅立葉變換在頻譜上時非週期的，離散時間傅立葉變換（DTFT）在頻譜上是週期的。在DSP中講了離散傅立葉變換，它的思想是將時域週期化，反映在頻域上就是對連續的週期頻譜進行抽樣

影象處理中傅立葉變換以及頻率域影象增強詳解

岡薩雷斯版<影象處理>裡面的解釋非常形象：一個恰當的比喻是將傅立葉變換比作一個玻璃稜鏡。稜鏡是可以將光分解為不同顏色的物理儀器，每個成分的顏色由波長（或頻率）來決定。傅立葉變換可以看作是數學上的稜鏡，將函式基於頻率分解為不同的成分。當我們考慮光時,討論它的光譜

影象的離散傅立葉變換

close all, clear, clc warning off all img_w = 640; img_h = img_w; xOfCenter = img_w / 2; yOfCenter = img_h / 2; %% DFT of oblique rectang

離散傅立葉變換（DFT）和快速傅立葉變換（FFT）原理與實現

目錄 1、影象變換 2、離散傅立葉變換（Discrete Fourier Transform） 3、DFT性質 4、DFT與數字影象處理 5、FFT-快速傅立葉變換 6、DFT與FFT的演算法實現 1. 影象變換 — —數學領域中有很多種變換，如傅立葉變換、拉普拉斯變

拉普拉斯變換，傅立葉變換；Z變換，離散時間傅立葉變換（DTFT）；離散傅立葉變換（DFT）之間的關係及理解

頻域與時域之間的關係是： 時域離散——頻域週期； 時域週期——頻域離散； 對於連續時間訊號 1.拉普拉斯變換： X (

離散傅立葉變換（DFT）

用途：將一組時域訊號變換到頻域，分析該訊號中各頻率分量。 效果：長度為n的數列x 的DFT是另一組長度為n的數列y yp+1=∑j=0n−1ωjpxj+1 其中，ω=e−2πi/n,p∈[0,n−

離散傅立葉變換（DTFT） MATLAB例項

w = [0:1:500]*pi/500; X= exp(1i*w) ./ (exp(1i*w) - 0.5*ones(1,501));        %ones : Create array of all ones magX= abs(X); angX = angle(X); realX =

實數序列離散傅立葉變換（DFT）的共軛對稱性質

先在matlab中執行以一命令，觀察一下結果：  >> b=[1 2 3 4 5 6 7 8] b =      1     2     3     4     5     6     7     8 >> fft(b) ans =   Column

理解離散傅立葉變換（一. 傅立葉變換的由來）

理解離散傅立葉變換（一）                      ------傅立葉變換的由來 關於傅立葉變換，無論是書本還是在網上可以很容易找到關於傅立葉變換的描述，但是大都是些故弄玄虛的文章，太過抽象，盡是一些讓人看了就望而生畏的公式的羅列，讓人很難能夠從感性上得到理解

【 MATLAB 】離散傅立葉變換（DFT）以及逆變換（IDFT）的MATLAB實現

剛剛寫過一篇用MATLAB實現離散傅立葉級數的博文，如下： 離散傅立葉變換不是一種神奇的東西，它和離散傅立葉級數關係很緊密，緊密到使用MATLAB編寫離散傅立葉變換以及逆變換的函式一模一樣，只需改個名字即可。 因為離散傅立葉級數是一個週期的訊號，我們編寫DFS以及ID

如何理解離散傅立葉變換（一）實數形式傅立葉變換

如何理解離散傅立葉變換（一） ——實數形式傅立葉變換 -----------------------------------------------------------------------------------------------------------

c語言數字影象處理（六）：二維離散傅立葉變換

基礎知識 複數表示 C = R + jI 極座標：C = |C|(cosθ + jsinθ) 尤拉公式：C = |C|ejθ 有關更多的時域與複頻域的知識可以學習複變函式與積分變換，本篇文章只給出DFT公式，性質，以及實現方法 二維離散傅立葉變換(DFT) 其中f(x,y)為原影象，F(u,

數字影象處理成長之路4： C語言與離散傅立葉變換(DFT)

這幾天一直學習傅立葉變換，看了很多國內外資料，網上講原理的很多，到了程式實現這塊大多是Matlab，opencv等，這些軟體的api對於我們理解DFT在計算機中的實現並沒有多大幫助。於是想用C/C++實現DFT，經過不斷的閱讀與程式設計實驗，最終程式有了還算滿意

離散傅立葉變換在影象處理中的應用_學習

1、為什麼要進行傅立葉變換，其物理意義是什麼？ 傅立葉原理表明：任何連續測量的時序或訊號，都可以表示為不同頻率的正弦波訊號的無限疊加。而根據該原理創立的傅立葉變換演算法利用直接測量到的原始訊號，以累加方式來計算該訊號中不同正弦波訊號的頻率、振幅和相位。 和傅立葉

數字影象處理，讀懂頻域處理的“傅立葉變換”

轉載自：https://blog.csdn.net/ebowtang/article/details/39004979 以下部分文字資料整合於網路，本文僅供自己學習用！ 這是一幅很絕的一維傅立葉變換動態圖 一，讀懂傅立葉變換 一個訊號能表示成傅立葉級數

數字影象處理之二維影象的傅立葉變換（1）

1.1、訊號變化越快，說明頻率越大，訊號變化越慢，說明頻率越小。這裡的頻率不一定是通常意義上的頻率，通常的頻率是指週期的倒數，我們把通常意義上的頻率叫時間頻率。廣義上的頻率是指變化的快慢，比如圖片來說，從這個畫素到另外一個畫素的灰度值差距比較大，那麼頻率就比較高

OpenCV中對影象進行二維離散傅立葉變換

#include<opencv2/opencv.hpp> #include <highgui.h> #include <iostream> #include <cv.h> #include <opencv2/core/c

影象傅立葉變換（二維離散傅立葉變換）

影象傅立葉變換 二維離散傅立葉變換是將影象從空間域轉至頻域，在影象增強、影象去噪、影象邊緣檢測、影象特徵提取、影象壓縮等等應用中都起著極其重要的作用。理論基礎是任意函式都可以表示成正弦函式的線性組合的形式。公式如下 逆變換公式如下 令 R(u,v) 和 I(u,c) 分別表示 F