1.L2正則化(嶺回歸)

1.1問題

想要理解什麽是正則化，首先我們先來了解上圖的方程式。當訓練的特征和數據很少時，往往會造成欠擬合的情況，對應的是左邊的坐標；而我們想要達到的目的往往是中間的坐標，適當的特征和數據用來訓練；但往往現實生活中影響結果的因素是很多的，也就是說會有很多個特征值，所以訓練模型的時候往往會造成過擬合的情況，如右邊的坐標所示。

1.2公式

以圖中的公式為例，往往我們得到的模型是：

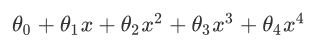
為了能夠得到中間坐標的圖形，肯定是希望θ3和θ4越小越好，因為這兩項越小就越接近於0，就可以得到中間的圖形了。

對應的損失函數也加上這個懲罰項(為了懲罰θ)：假設λ=1000

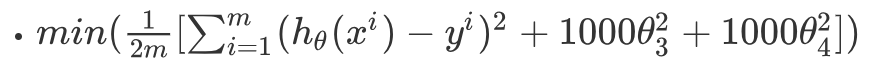
為了求得最小值，使θ值趨近於0

把以上公式通用化得：

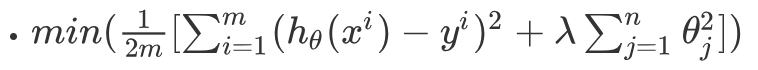
相當於在原始損失函數中加上了一個懲罰項(λ項)

這就是防止過擬合的一個方法，通常叫做L2正則化，也叫作嶺回歸。

1.3對應圖形

我們可以簡化L2正則化的方程：

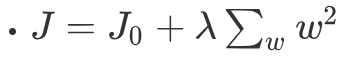
J0表示原始的損失函數，咱們假設正則化項為：

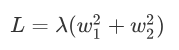
我們不妨回憶一下圓形的方程：

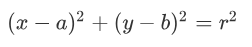
其中(a,b)為圓心坐標，r為半徑。那麽經過坐標原點的單位元可以寫成：

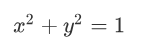
正和L2正則化項一樣，同時，機器學習的任務就是要通過一些方法（比如梯度下降）求出損失函數的最小值。

此時我們的任務變成在L約束下求出J0取最小值的解。

求解J0的過程可以畫出等值線。同時L2正則化的函數L也可以在w1w2的二維平面上畫出來。如下圖：

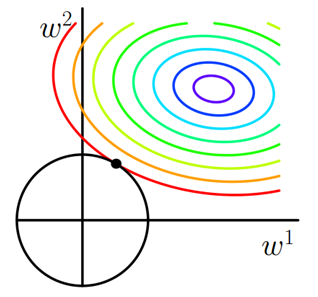
L表示為圖中的黑色圓形，隨著梯度下降法的不斷逼近，與圓第一次產生交點，而這個交點很難出現在坐標軸上。

這就說明了L2正則化不容易得到稀疏矩陣，同時為了求出損失函數的最小值，使得w1和w2無限接近於0，達到防止過擬合的問題。

1.4使用場景

只要數據線性相關，用LinearRegression擬合的不是很好，需要正則化，可以考慮使用嶺回歸(L2), 如何輸入特征的維度很高,而且是稀疏線性關系的話， 嶺回歸就不太合適,考慮使用Lasso回歸。

1.5代碼實現

GitHub代碼--L2正則化

2.L1正則化(lasso回歸)

2.1公式

L1正則化與L2正則化的區別在於懲罰項的不同：

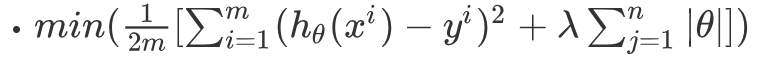
L1正則化表現的是θ的絕對值，變化為上面提到的w1和w2可以表示為：

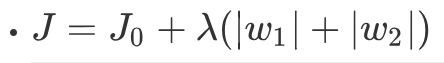
2.2對應圖形

求解J0的過程可以畫出等值線。同時L1正則化的函數也可以在w1w2的二維平面上畫出來。如下圖：

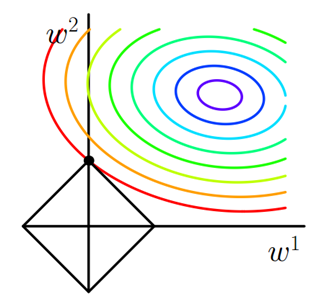
懲罰項表示為圖中的黑色棱形，隨著梯度下降法的不斷逼近，與棱形第一次產生交點，而這個交點很容易出現在坐標軸上。這就說明了L1正則化容易得到稀疏矩陣。

2.3使用場景

L1正則化(Lasso回歸)可以使得一些特征的系數變小,甚至還使一些絕對值較小的系數直接變為0，從而增強模型的泛化能力 。對於高緯的特征數據,尤其是線性關系是稀疏的，就采用L1正則化(Lasso回歸),或者是要在一堆特征裏面找出主要的特征，那麽L1正則化(Lasso回歸)更是首選了。

2.4代碼實現

GitHub代碼--L1正則化

3.ElasticNet回歸

3.1公式

ElasticNet綜合了L1正則化項和L2正則化項，以下是它的公式：

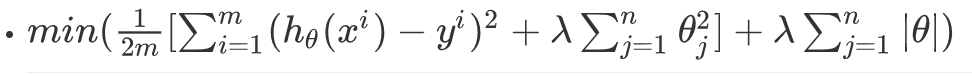
3.2使用場景

ElasticNet在我們發現用Lasso回歸太過(太多特征被稀疏為0),而嶺回歸也正則化的不夠(回歸系數衰減太慢)的時候，可以考慮使用ElasticNet回歸來綜合，得到比較好的結果。

3.3代碼實現

from sklearn import linear_model  
#得到擬合模型，其中x_train,y_train為訓練集  
ENSTest = linear_model.ElasticNetCV(alphas=[0.0001, 0.0005, 0.001, 0.01, 0.1, 1, 10], l1_ratio=[.01, .1, .5, .9, .99],  max_iter=5000).fit(x_train, y_train)  
#利用模型預測，x_test為測試集特征變量  
y_prediction = ENSTest.predict(x_test)

.

.

.

歡迎添加微信交流！請備註“機器學習”。

通俗易懂--嶺回歸(L2)、lasso回歸(L1)、ElasticNet講解(算法+案例)