二叉查詢樹常常會考到和使用到，本文練習下它的幾個基本操作，即節點的查詢、插入和刪除及找最大值、最小值等。

1，二叉查詢樹的查詢
由於二叉查詢樹的性質是，每個節點的關鍵字值大於其左子樹的所有節點，同時小於右子樹的所有節點。因此查詢就可以利用其性質來進行。
實現程式碼如下：

/* node struct */
class node
{
public:
    int value;
    node* left;
    node* right;
};

node* find(node* root, const int key)
{
    if (NULL == root)
    {
        return
 
 NULL;
    }

    node* pos = root;

    while(NULL != pos)
    {
        if (key == pos -> value)
        {
            break;
        }
        else if (key < pos -> value)
        {
            pos = pos -> left;
        }
        else
        {
            pos = pos -> right;
        }
    }

    return
 
 pos;
}

2，二叉查詢樹找最大節點和最小節點
同樣，利用二叉查詢樹的性質，有以下實現程式碼：

node* find_max(node* root)
{
    if (NULL == node)
    {
        return NULL;
    }

    node* pos = root;

    while (NULL !＝ pos -> right)
    {
        pos = pos -> right;
    }

    return pos;
}

node* find_min(node* root)
{
    if (NULL
 
 == root)
    {
        return NULL;
    }

    node* pos = root;

    if (NULL != root -> left)
    {
        pos = pos -> left;
    }

    return pos;
}

3，二叉查詢樹的插入
往二叉查詢樹插入一個節點，需要保持二叉查詢樹的性質，因此一種插入的思想是運用二叉查詢樹的查詢思想，查詢新關鍵字應該放在樹中的哪個位置，具體的實現程式碼如下（通過下面程式碼，可以知道在樹中可以很方便的通過遞迴來實現相關操作）：

node* insert(node* root, const int key)
{
    if (NULL == root)
    {
        root = new node;
        if (NULL == root)
        {
            return NULL;
        }
        root -> value = key;
        root -> left = NULL;
        root -> right = NULL;
        return root;
    }

    if (key < pos -> value)
    {
        root -> left = insert(root -> left, key);
    }
    else
    {
        root -> right = insert(root -> right, key);
    }

    return root;
}

4，最後看下二叉查詢樹的刪除
刪除分兩種情況，一種是被刪節點有一個子節點或0個子節點，另一種是被刪子節點有兩個子節點。對於前一種情況，處理較為簡單，直接刪除相應節點，若其有一個子節點，則將該子節點掛載到相應節點的父節點上；對於第二種情況，處理更復雜一些，一種處理方式是，將該節點的右子樹的最小節點的關鍵字賦給當前節點，隨後遞迴的在右子樹中刪除該最小節點，這樣會一直遞迴到被刪除的節點只有一個子節點或沒有子節點。
在《資料結構與演算法分析》上截兩個刪除示意圖如下：


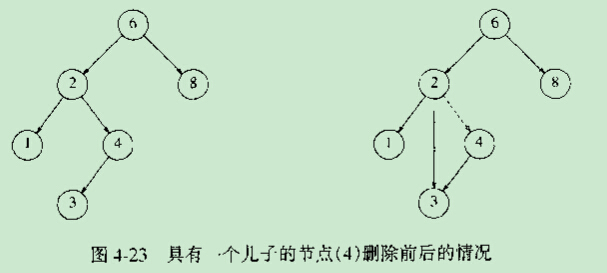
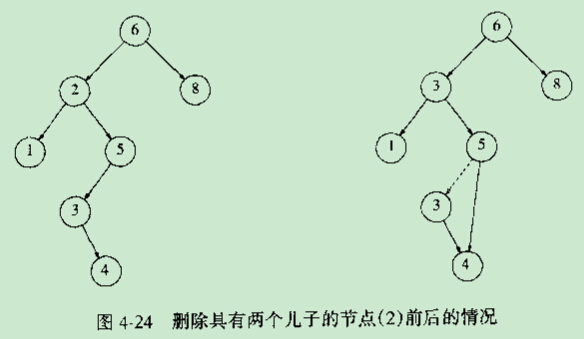
具體實現程式碼如下：

node* delete(node* root, const int key)
{
    if (NULL ＝＝ root)
    {
        return NULL;
    }

    node* pos = NULL;

    if (key < root -> value)
    {
        root -> left = delete(root -> left, key);
    }
    else if (key > root -> value)
    {
        root -> right = delete(root -> right, key);
    }
    else    // find the node
    {
        if (NULL != root -> left && NULL != root -> right)
        {
            pos = find_min(root -> right);
            root -> value = pos -> value;
            root -> right = delete(root -> right, root -> value);
        }
        else
        {
            pos = root;
            if (NULL != root -> left)
            {
                root = root -> left;
            }
            else if (NULL != root -> right)
            {
                root = root -> right;
            }

            delete pos;
            pos = NULL;
        }
    }

    return root;
}