演算法導論-----最長公共子序列LCS（動態規劃）

一.概念梳理

1. 子序列(subsequence)：一個特定序列的子序列就是將給定序列中零個或多個元素去掉後得到的結果(不改變元素間相對次序)。例如序列<A,B,C,B,D,A,B>的子序列有：<A,B>、<B,C,A>、<A,B,C,D,A>等。
2.公共子序列(common subsequence)：給定序列X和Y，序列Z是X的子序列，也是Y的子序列，則Z是X和Y的公共子序列。例如X=<A,B,C,B,D,A,B>，Y=<B,D,C,A,B,A>，那麼序列Z=<B,C,A>

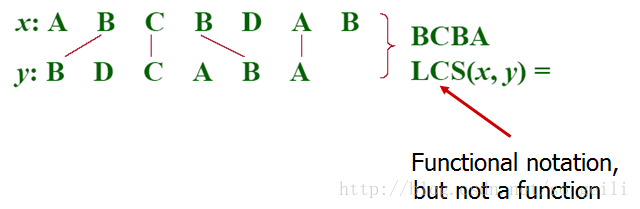
為X和Y的公共子序列，其長度為3。但Z不是X和Y的最長公共子序列，而序列<B,C,B,A>和<B,D,A,B>也均為X和Y的最長公共子序列，長度為4，而X和Y不存在長度大於等於5的公共子序列。
3.最長公共子序列問題(LCS:longest-common-subsequence problem)：In the longest-common-subsequence problem, we are given two sequences X=<x1,x2,...,xm> and Y=<y1,y2,...,yn> and wish to find a (not “the”)

maximum-length common subsequence of X and Y . This section shows how to efficiently solve the LCS problem using dynamic programming.

二.最長公共子序列解決方案

方案1：蠻力搜尋策略

蠻力搜尋策略的步驟如下：

列舉序列X裡的每一個子序列xi；
檢查子序列xi是否也是Y序列裡的子序列；
在每一步記錄當前找到的子序列裡面的最長的子序列。

蠻力策略也叫做暴力窮舉法，是所有演算法中最直觀的方法，但效率往往也是最差的。在第1步列舉X中所有的子序列有2

m個，每個子序列在Y中檢查時間複雜度為O(n)。因此蠻力策略的最壞時間複雜度為O(n2m)，這是指數級演算法，對較長的序列求LCS是不適用的。

方案2：動態規劃策略

LCS問題具有最優子結構
令 X=<x1,x2,...,xm> 和 Y=<y1,y2,...,yn> 為兩個序列，Z=<z1,z2,z3,...,zk>為X和Y的任意LCS。則

如果xm=yn，則zk=xm=yn且Zk−1是Xm−1和Yn−1的一個LCS。
如果xm≠yn，那麼zk≠xm，意味著Z是Xm−1和Y的一個LCS。
如果xm≠yn，那麼zk≠yn，意味著Z是X和Y

相關推薦

演算法導論-----最長公共子序列LCS（動態規劃）

目錄一.概念梳理 1. 子序列(subsequence)：一個特定序列的子序列就是將給定序列中零個或多個元素去掉後得到的結果(不改變元素間相對次序)。例如序列<A,B,C,B,D,A,B>的子序列有：<A,B>、&l

【51nod】---1006 最長公共子序列Lcs（動態規劃&&字串LCS）

題目連結這裡呀 1006 最長公共子序列Lcs 基準時間限制：1 秒空間限制：131072 KB 分值: 0 難度：基礎題收藏關注給出兩個字串A B，求A與B的最長公共子序列（子序列不要求是連續的）。比如兩個串為： abcicba abd

最長公共子序列Lcs （51Nod - 1006）

string OS 模板題 != std ring str spa sin 20180604 11:28 給出兩個字符串A B，求A與B的最長公共子序列（子序列不要求是連續的）。比如兩個串為： abcicba abdkscab ab是兩個串的子序列

Prince and Princess（最長公共子序列優化，動態規劃）

<a target=_blank href="https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&

動態規劃演算法解最長公共子序列LCS問題

原文地址：http://blog.csdn.net/rrrfff/article/details/7523437 動態規劃演算法解LCS問題作者 July 二零一零年十二月三十一日本文參考：

演算法分析—最長公共子序列(LCS)

子序列：給定一個序列X={x1,x2,…,xm}，另一個序列Z={z1,z2,…,zk}，即存在一個嚴格遞增的X的下標序列{i1,i2,…,ik},對於所有的j=1,2,3…,k,滿足xij=zj,我

從最長公共子序列問題理解動態規劃演算法（DP）

# 一、動態規劃(Dynamic Programming) 動態規劃方法通常用於求解**最優化問題**。我們希望找到一個解使其取得最優值，而不是所有最優解，可能有多個解都達到最優值。 # 二、什麼問題適合DP解法如何判斷一個問題是不是DP問題呢？適合DP求解的最優化問題通常具有以下兩個特徵： * *

最長公共子序列問題和動態規劃

最長子序列問題子序列定義可以注意到,子序列不要求所選的字母連續,只要求是按原次序組成就好這是和子串的一個區別最長公共子序列定義最長公共子序列(L ongest C ommon S equence) 簡稱為LCS,下同

最大連續子序列之和（動態規劃）

1. 問題描述設n個元素的序列儲存在陣列A[0..n-1]中，求陣列中連續子序列之和的最大值。 2. 遞推公式設All[i]為子問題A[i..n-1]的連續子序列之和的最大值，start[i]為從A[i]開始的連續序列之和的最大值，因此： All[i] = A[n-

演算法學習筆記最長公共子序列LCS

給定兩個字串，求最長公共子序列及其長度（不同於最長公共子串的是公共子串要求連續）思路：設字串為a,b 建立二維陣列c用於打表，建立二維陣列d，用於記錄路徑，其中c[i][j]表示的是a的前i個字元構成的字串和b的前j個字元構成的字串的最大公共字串的和，則分析題目得狀態

演算法課堂實驗報告（四）——python動態規劃（最長公共子序列LCS問題）

python實現動態規劃一、開發環境開發工具：jupyter notebook 並使用vscode，cmd命令列工具協助程式設計測試演算法,並使用codeblocks輔助編寫C++程式程式語言：python3.6 二、實驗內容 1.最長公共子序列問題。分別求x=

最長公共子序列LCS和最長迴文子序列的動態規劃演算法

c[i][j] 用來表示 x[i] 和y[j] 的LCS 長度對c[i][j]，若i = 0或j = 0，則c[i][j] = 0，兩個原序列有一個為空，則沒有LCS；若i,j > 0 且x[i] = y[j]，則c[i][j] = c[i-1][j-1] +

最長公共子序列LCS (DP)

mem main amp code bcd max std pan ems 題意：求兩個字符串的公共子序列，如“abcd” 與 “becd”的公共子序列是 “bcd” 分析：設兩個字符串為串s 和串tdp[i][j]:= s1..si和t1...tj對應的LCS長度

51nod 1006 最長公共子序列Lcs(dp+string,無標記數組實現)

轉移 opened mes star 字符 tex src 表示 logs 1006 最長公共子序列Lcs 基準時間限制：1 秒空間限制：131072 KB 分值: 0 難度：基礎題收藏關註取消關註給出兩個字符串A B，求A與B的最長公共子序

1006 最長公共子序列Lcs

scan gray 16px 最長公共子序列 pre std pri 第一個 put 給出兩個字符串A B，求A與B的最長公共子序列（子序列不要求是連續的）。比如兩個串為： abcicba abdkscab ab是兩個串的子序列，abc也是，abca也是，其中ab

最長公共子序列 LCS 遞歸 dp 51Nod 1006

要求 hid using col mes turn tdi bbb clas 給出兩個字符串A B，求A與B的最長公共子序列（子序列不要求是連續的）。比如兩個串為： abcicba abdkscab ab是兩個串的子序列，abc也是，abca也是，其中ab

最長公共子序列-LCS問題 (LCS與LIS在特殊條件下的轉換) [洛谷1439]

一個 har define 分享 amp lis read ios stack 題目描述給出1-n的兩個排列P1和P2，求它們的最長公共子序列。輸入第一行是一個數n，接下來兩行，每行為n個數，為自然數1-n的一個排列。輸出一個數，即最長公

最長公共子序列(LCS)

() 參考資料 ... void 表格 abc src size charat 最長公共子序列問題在算法導論中引申自確定DNA序列相似度的問題：給定兩個DNA序列S1和S2，尋找第三個序列S3，要求序列S3中的元素都來源於S1和S2，且在這三個序列中先後順序相同，但在S1和

動態規劃-最長公共子序列LCS

return str2 pat for 思路規劃得來表示 || 0 問題給定兩個字符串，求最長公共子序列LCS。也就是說兩個字符串中都有的部分，或者理解為，兩個字符串同時都刪除字符串中的某些字符，使得最終的兩個字符串，相等，且是最長的。 1 分析假設兩個str1

最長公共子序列LCS

chang 因此數據超過 ear print () 哪些 class 1 public class Zuichangzixulie { 2 //X[n] 取哪些 3 //Y[m] 取哪些 4 // int search(int xi, i