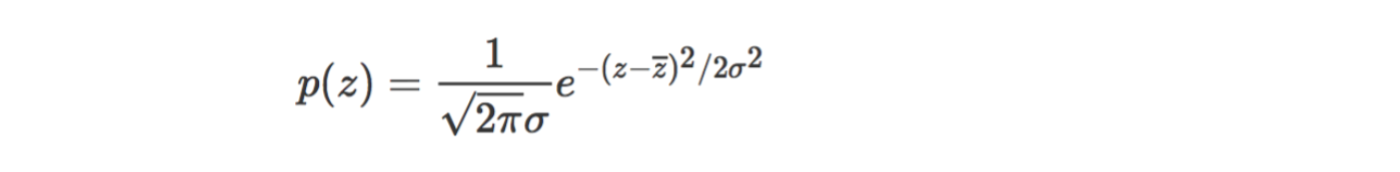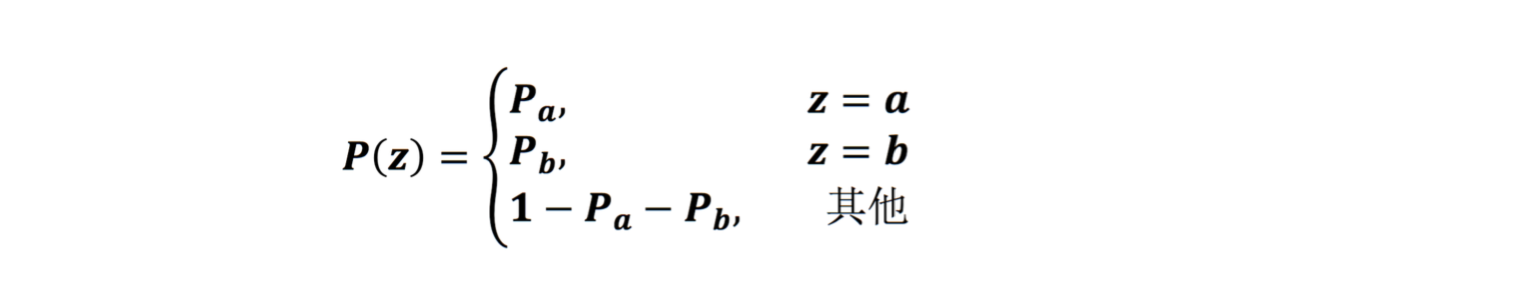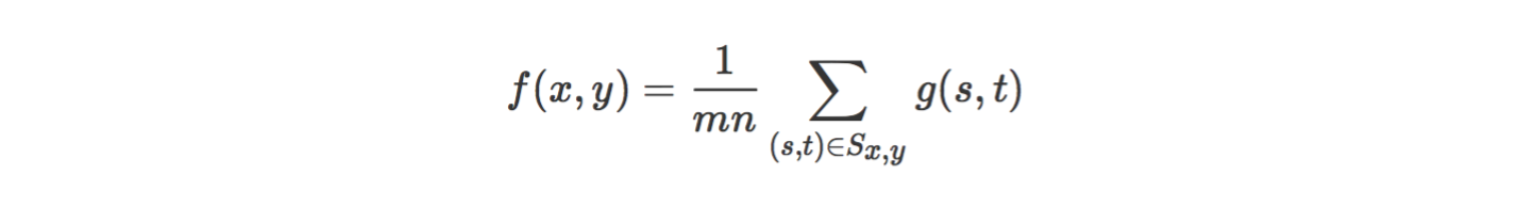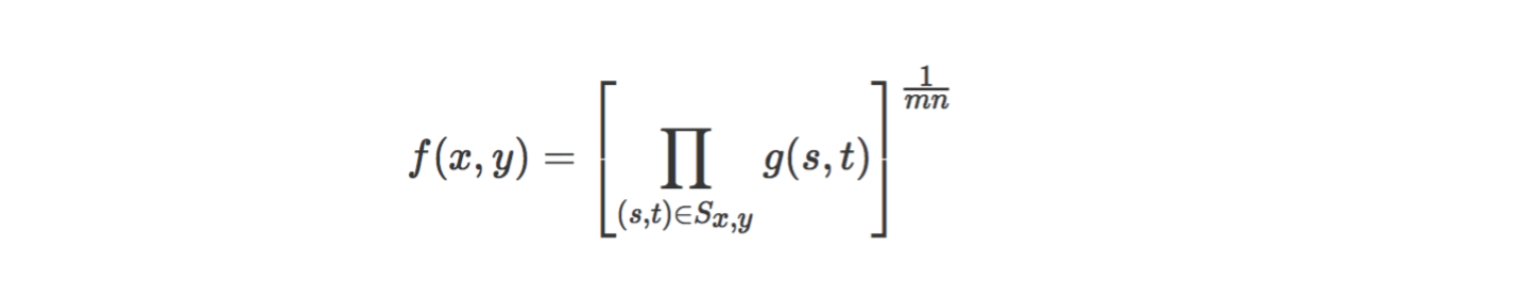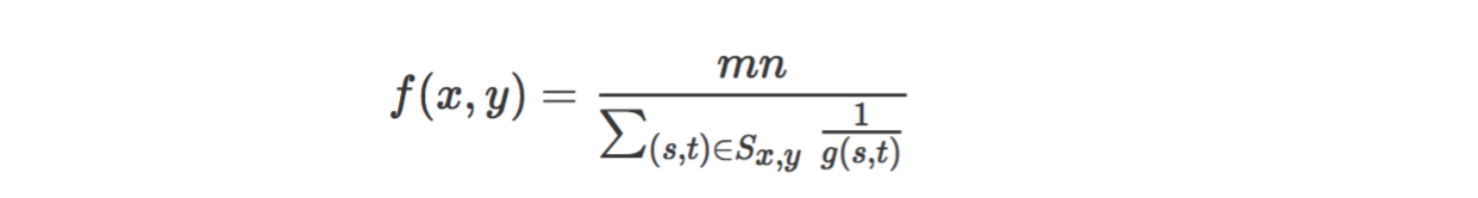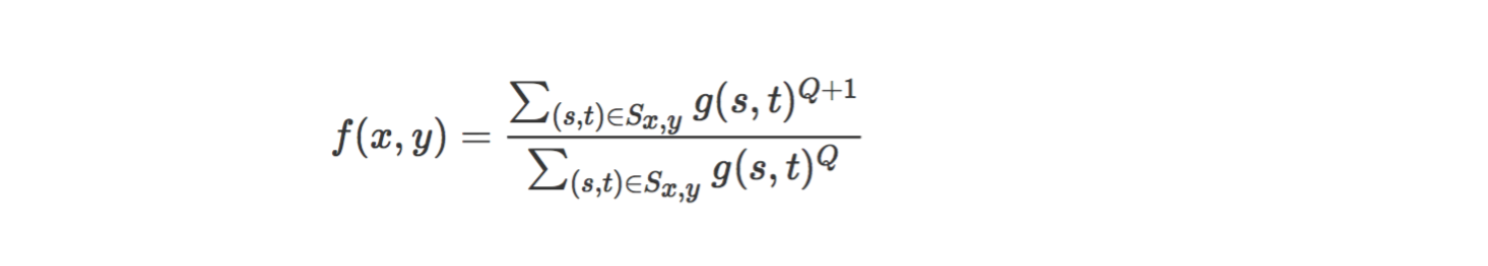最近交了數圖作業，mark一下。

1.新增高斯噪聲

1.1 概率密度函式

σ為z的標準差,z為均值,用E。

1.2 生成高斯分佈隨機數序列

方法由Marsaglia和Bray在1964年提出,C++版本如下: mu是均值,sigma是方差,X服從N(0,1)分佈

double generateGaussianNoise(double mu, double sigma)
{
    static double V1, V2, S;
    static int phase = 0;
    double X;
    double U1,U2;
    if ( phase == 0
 
 ) {
        do {
            U1 = (double)rand() / RAND_MAX;
            U2 = (double)rand() / RAND_MAX;

            V1 = 2 * U1 - 1;
            V2 = 2 * U2 - 1;
            S = V1 * V1 + V2 * V2;
        } while(S >= 1 || S == 0);

        X = V1 * sqrt(-2 * log(S) / S);
    } else{
        X = V2 * sqrt
 
(-2 * log(S) / S);
    }
    phase = 1 - phase;
    return mu+sigma*X;
}

1.3 新增高斯噪聲

高斯噪聲為加性噪聲,在原圖的基礎上加上噪聲即為加噪後的圖象。
程式碼如下:

void AddNoise(Mat img,double mu, double sigma,int k){
    Mat outImage;
    outImage.create(img.rows,img.cols,img.type());
    for(int x=0;x<img.rows;x++){
        for(int
 
 y=0;y<img.cols;y++){
            double temp = img.at<uchar>(x, y)
                    +k*generateGaussianNoise(mu,sigma);
            if(temp>PixcelMax)
                    temp=PixcelMax;
            else if(temp<PixcelMin)
                    temp=PixcelMin;
            outImage.at<uchar>(x, y) = temp;
        }
    }
    Filter(outImage,Filter::NXBJZ,3,3,1);
    imshow("Output", outImage);
    cvWaitKey(0);
}

1.4 效果圖

如圖,k為高斯噪聲的係數,係數越大,高斯噪聲越強。

噪聲服從高斯分佈,所以方差越大,資料越分散,噪聲也就越多。

均值決定著整個影象的明亮程度,均值大於0,表示影象加上一個使自己變亮的噪聲,小 於0,表示影象加上一個使自己變暗的噪聲。

2.新增椒鹽噪聲

2.1 概率密度函式

2.2 新增椒鹽噪聲

椒鹽噪聲是根據影象的信噪比,隨機生成一些影象內的畫素位置,並隨機對這些畫素點賦值為0或255.

程式碼如下：

void AddNoise(Mat img,double SNR ){
    Mat outImage;
    outImage.create(img.rows,img.cols,img.type());
    int SP = img.rows*img.cols;
    int NP = SP*(1-SNR);
    outImage = img.clone();
    for(int i=0; i<NP; i++) {

        int x = (int)(rand()*1.0/RAND_MAX* (double)img.rows);
        int y = (int)(rand()*1.0/RAND_MAX* (double)img.cols);
        int r = rand()%2;
       if(r){
            outImage.at<uchar>(x, y)=0;
        }
       else{
           outImage.at<uchar>(x, y)=255;
       }

    }
     Filter(outImage,Filter::NXBJZ,3,3,1);
    imshow("Output", outImage);
    cvWaitKey(0);
}

其中,SNR為信噪比,利用C++中的rand() 作為隨機函式。

2.3 效果圖

信噪比越小,噪聲越多,信噪比為1時,影象不含噪聲。 0為胡椒噪聲,255為鹽粒噪聲

3.均值濾波器

3.1 算術均值濾波器

Sx,y為以(x,y)為中心,長為m寬為n的矩形範圍。

3.1.1 濾除高斯噪聲

3.1.2濾除椒鹽噪聲

總結:
只能在噪聲較少的情況下去除些許噪聲,並且只是平滑了影象的區域性變化,令影象變得模
糊。

3.2 幾何均值濾波器

Sx,y為以(x,y)為中心,長為m寬為n的矩形範圍。

3.2.1 濾除高斯噪聲

3.2.2 濾除椒鹽噪聲

總結:
處理高斯噪聲時,噪聲較少時,效果與算術均值濾波器基本一致。但是噪聲較多時,
會對灰度值較小的噪聲進行放大,導致影象出現許多黑點,使影象變暗。
處理椒鹽噪聲時,會對胡椒噪聲放大,導致影象出現許多黑點,而對鹽粒噪聲有較好
的濾除作用。

3.3 諧波均值濾波器

3.3.1 濾除高斯噪聲

3.3.2濾除椒鹽噪聲

總結:
與幾何均值濾波器有相似的效果,處理高斯噪聲時,會對灰度值較小的噪聲進行放
大,導致影象出現許多黑點,使影象變暗。
處理椒鹽噪聲時,會對胡椒噪聲放大,導致影象出現許多黑點,無法處理胡椒噪聲,
而對鹽粒噪聲有較好的濾除作用。

3.4 逆諧波均值濾波器

3.4.1 濾除高斯噪聲

3.4.2濾除椒鹽噪聲

總結:
Q為正時,會對灰度值較大的噪聲進行放大,Q為負時,會對灰度值較小的噪聲進行 放大。
處理椒鹽噪聲時,Q為正,對胡椒噪聲有較好的濾除作用,Q為負,對鹽粒噪聲有較 好的濾除作用。

程式碼如下：

void Filter(Mat img,Filter f,int m,int n,int Q = 0){
    Mat outImage;
    outImage.create(img.rows,img.cols,img.type());
    int h = m/2,w=n/2;
    for(int x=0;x<img.rows;x++){
        for(int y=0;y<img.cols;y++){
            int cnt = 0;
            if(f== Filter::SSJZ){
                long double sum = 0;
                for(int i=x-h;i<=x+h;i++){
                    for(int j=y-w;j<=y+w;j++){
                        if(i<0||i>=img.rows||j<0||j>=img.cols)continue;
                        cnt++;
                        sum+=img.at<uchar>(i, j);
                    }
                }
                outImage.at<uchar>(x, y)=sum/cnt;
            }
            else if(f== Filter::JHJZ){
                long double sum = 1;
                for(int i=x-h;i<=x+h;i++){
                    for(int j=y-w;j<=y+w;j++){
                        if(i<0||i>=img.rows||j<0||j>=img.cols)continue;
                        cnt++;
                        sum*=img.at<uchar>(i, j);
                    }
                }
                outImage.at<uchar>(x, y)=pow(sum,1.0/cnt);
            }
            else if(f== Filter::XBJZ){
                long double sum = 0;
                for(int i=x-h;i<=x+h;i++){
                    for(int j=y-w;j<=y+w;j++){
                        if(i<0||i>=img.rows||j<0||j>=img.cols)continue;
                        cnt++;
                        sum+=1.0/img.at<uchar>(i, j);
                    }
                }
                outImage.at<uchar>(x, y)=cnt/sum;
            }
            else if(f== Filter::NXBJZ){
                long double sum1 = 0,sum2 = 0;
                for(int i=x-h;i<=x+h;i++){
                    for(int j=y-w;j<=y+w;j++){
                        if(i<0||i>=img.rows||j<0||j>=img.cols)continue;
                        cnt++;
                        sum1+=pow(img.at<uchar>(i, j),Q);
                        sum2+=pow(img.at<uchar>(i, j),Q+1);
                    }
                }
                outImage.at<uchar>(x, y)=sum2/sum1;
            }
        }
    }
    imshow("Output", outImage);
    imwrite("/Users/camellia/desktop/gaussnoise_NXBJZ.jpg", outImage);
    cvWaitKey(0);
}

2017.7.31更新——
補充
四種濾波器
SSJZ——算術均值濾波器
JHJZ——幾何均值濾波器
XBJZ——諧波均值濾波器
NXBJZ——逆諧波均值濾波器

enum Filter{
    SSJZ,JHJZ,XBJZ,NXBJZ
};
int main()
{

    Mat image;
    image = imread("/Users/camellia/desktop/lena.jpg",0);// 測試圖片路徑
    if ( !image.data )
    {
        printf("No image data \n");
        return -1;
    }
    namedWindow("Display Image", WINDOW_AUTOSIZE );
    imshow("Display Image", image);
    imwrite("/Users/camellia/desktop/origin.jpg", image);

    waitKey(0);
  // AddNoise(image,0,1,64);
     AddNoise(image,0.98);
//     Filter(image,SSJZ,5,5);
//     Filter(image,JHJZ,5,5);
//     Filter(image,XBJZ,5,5);
//     Filter(image,NXBJZ,5,5);
    return 0;
}