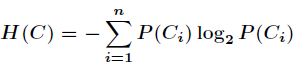Spark2.0機器學習系列之3：決策樹及Spark 2.0-MLlib、Scikit程式碼分析

阿新 • • 發佈：2019-01-07

概述

分類決策樹模型是一種描述對例項進行分類的樹形結構。決策樹可以看為一個if-then規則集合，具有“互斥完備”性質。決策樹基本上都是採用的是貪心（即非回溯）的演算法，自頂向下遞迴分治構造。
生成決策樹一般包含三個步驟：
- 特徵選擇
- 決策樹生成
- 剪枝

決策樹演算法種類

決策樹主要有 ID3, C4.5, C5.0 and CART幾種， ID3, C4.5, 和CART實際都採用的是貪心（即非回溯）的演算法，自頂向下遞迴分治構造。對於每一個決策要求分成的組之間的“差異”最大。各種決策樹演算法之間的主要區別就是對這個“差異”衡量方式的區別。
ID3和CART方法大約同時獨立發明，形成了決策樹歸納研究的基礎。

ID3請參考：http://blog.csdn.net/acdreamers/article/details/44661149
在資訊理論中，期望資訊越小，那麼資訊增益就越大，從而純度就越高。ID3演算法的核心思想就是以資訊增益來度量屬性的選擇，選擇分裂後資訊增益最大的屬性進行分裂。該演算法採用自頂向下的貪婪搜尋遍歷可能的決策空間。

     在資訊增益中，重要性的衡量標準就是看特徵能夠為分類系統帶來多少資訊，帶來的資訊越多，該特徵越  重要。在認識資訊增益之前，先來看看資訊熵的定義(每一個類別的概率是P(Ci))

這裡寫圖片描述

       熵這個概念最早起源於物理學，在物理學中是用來度量一個熱力學系統的無序程度，而在資訊學裡面，熵是對不確定性的度量。在1948年，夏農引入了資訊熵，將其定義為離散隨機事件出現的概率，一個系統越是有序，資訊熵就越低，反之一個系統越是混亂，它的資訊熵就越高。所以資訊熵可以被認為是系統有序化程度的一個度量。

C4.5:是在ID3決策樹的基礎之上進行改進，C4.5克服了ID3的2個缺點：
（1）用資訊增益選擇屬性時偏向於選擇分枝比較多的屬性值，即取值多的屬性
（2）不能處理連貫屬性
C4.5是這樣做的：
（1）選取能夠得到最大資訊增益率（information gain ratio）的特徵來劃分資料，並且像ID3一樣執行後剪枝。也就是說採用比率，能較好解決ID3的第（1）個缺點
（2）當特徵數值連續時，在分類的時候進行離散化。

C5.0是Quinlan最新發布版本的決策樹演算法，需要專利授權。相對於C 4.5而言，該方法計算時佔用記憶體更少，建立了更小的規則集，計算結果也更加準確。C5.0演算法由於執行效率和記憶體使用改進、適用大資料集。C5.0演算法選擇分支變數的依據：以資訊熵的下降速度作為確定最佳分支變數和分割閥值的依據。資訊熵的下降意味著資訊的不確定性下降。

    （1）ID3 (Iterative Dichotomiser 3) was developed in 1986 by Ross Quinlan. The algorithm creates a multiway tree, finding for each node (i.e. in a greedy manner) the categorical feature that will yield the largest information gain for categorical targets. Trees are grown to their maximum size and then a pruning step is usually applied to   improve the ability of the tree to generalise to unseen data.
    （2）C4.5 is the successor to ID3 and removed the restriction that features must be categorical by dynamically defining a discrete attribute (based on numerical variables) that partitions the continuous attribute value into a discrete set of intervals. C4.5 converts the trained trees (i.e. the output of the ID3 algorithm) into sets of if-then rules. These accuracy of each rule is then evaluated to determine the order in which they should be applied. Pruning is done by removing a rule’s precondition if the accuracy of the rule improves without it.
    （3）C5.0 is Quinlan’s latest version release under a proprietary license. It uses less memory and builds smaller rulesets than C4.5 while being  more accurate.
    （4）CART (Classification and Regression Trees) is very similar to C4.5, but it differs in that it supports numerical target variables (regression) and does not compute rule sets. CART constructs binary trees using the feature and threshold that yield the largest information gain at each node.

它和C45基本上是類似的演算法，主要區別：1）它的葉節點不是具體的分類，而是是一個函式f()，該函式定義了在該條件下的迴歸函式。2）CART是二叉樹，而不是多叉樹。

Scikit中的決策樹

Spark MLlib決策樹程式碼詳細分析

Spark MLlib中決策樹 Spark2.0,基於DataFrame的API。
決策樹和決策樹的組合，是解決分類問題和迴歸問題比較流行的一類演算法。具備了諸多優點：
- 結果易於解釋；
- 可以處理類別特徵；
- 可以擴充套件到多分類；
- 不需要對特徵進行歸一化；
- 可以分析各feature之間的相互作用。
  隨機森林，boosting演算法都是決策樹的組合。
  Spark中決策樹可以解決二分類，多分類和迴歸問題，可以使用連續的和類別的特徵。由於資料集是按行進行分割槽的，可以對大型資料集（百萬甚至十億級的資料集）進行分散式訓練。
  
  （1）Decision trees and their ensembles are popular methods for the machine learning tasks of classification and regression. Decision trees are widely used since they are easy to interpret, handle categorical features, extend to the multiclass classification setting, do not require feature scaling, and are able to capture non-linearities and feature interactions. Tree ensemble algorithms such as random forests and boosting are among the top performers for classification and regression tasks.
  （2）The spark.ml implementation supports decision trees for binary and multiclass classification and for regression, using both continuous and categorical features. The implementation partitions data by rows, allowing distributed training with millions or even billions of instances.

在Spark Pipeline中編寫決策樹流程，以下三個特徵轉換器（Feature Transformers）常用，但不是特別好理解（結合本部分後面各自例子看吧）。
http://spark.apache.org/docs/latest/ml-features.html#vectorindexer

VectorIndexer

主要作用：提高決策樹或隨機森林等ML方法的分類效果。
VectorIndexer是對資料集特徵向量中的類別（離散值）特徵（index categorical features categorical features ）進行編號。
它能夠自動判斷那些特徵是離散值型的特徵，並對他們進行編號，具體做法是通過設定一個maxCategories，特徵向量中某一個特徵不重複取值個數小於maxCategories，則被重新編號為0～K（K<=maxCategories-1）。某一個特徵不重複取值個數大於maxCategories，則該特徵視為連續值，不會重新編號（不會發生任何改變）。結合例子看吧，實在太繞了。

VectorIndexer helps index categorical features in datasets of Vectors. It can both automatically decide which features are categorical and convert original values to category indices. Specifically, it does the following:

    Take an input column of type Vector and a parameter maxCategories. Decide which features should be categorical based on the number of distinct values, where features with at most maxCategories are declared categorical.
Compute 0-based category indices for each categorical feature.
Index categorical features and transform original feature values to indices.

    Indexing categorical features allows algorithms such as Decision Trees and Tree Ensembles to treat categorical features appropriately, improving performance.

    This transformed data could then be passed to algorithms such as DecisionTreeRegressor that handle categorical features.

用一個簡單的資料集舉例如下：

//定義輸入輸出列和最大類別數為5，某一個特徵
//（即某一列）中多於5個取值視為連續值
VectorIndexerModel featureIndexerModel=new VectorIndexer()
                 .setInputCol("features")
                 .setMaxCategories(5)
                 .setOutputCol("indexedFeatures")
                 .fit(rawData);
//加入到Pipeline
Pipeline pipeline=new Pipeline()
                 .setStages(new PipelineStage[]
                         {labelIndexerModel,
                         featureIndexerModel,
                         dtClassifier,
                         converter});
pipeline.fit(rawData).transform(rawData).select("features","indexedFeatures").show(20,false);
//顯示如下的結果：        
+-------------------------+-------------------------+
|features                 |indexedFeatures          |
+-------------------------+-------------------------+
|(3,[0,1,2],[2.0,5.0,7.0])|(3,[0,1,2],[2.0,1.0,1.0])|
|(3,[0,1,2],[3.0,5.0,9.0])|(3,[0,1,2],[3.0,1.0,2.0])|
|(3,[0,1,2],[4.0,7.0,9.0])|(3,[0,1,2],[4.0,3.0,2.0])|
|(3,[0,1,2],[2.0,4.0,9.0])|(3,[0,1,2],[2.0,0.0,2.0])|
|(3,[0,1,2],[9.0,5.0,7.0])|(3,[0,1,2],[9.0,1.0,1.0])|
|(3,[0,1,2],[2.0,5.0,9.0])|(3,[0,1,2],[2.0,1.0,2.0])|
|(3,[0,1,2],[3.0,4.0,9.0])|(3,[0,1,2],[3.0,0.0,2.0])|
|(3,[0,1,2],[8.0,4.0,9.0])|(3,[0,1,2],[8.0,0.0,2.0])|
|(3,[0,1,2],[3.0,6.0,2.0])|(3,[0,1,2],[3.0,2.0,0.0])|
|(3,[0,1,2],[5.0,9.0,2.0])|(3,[0,1,2],[5.0,4.0,0.0])|
+-------------------------+-------------------------+
結果分析：特徵向量包含3個特徵，即特徵0，特徵1，特徵2。如Row=1,對應的特徵分別是2.0,5.0,7.0.被轉換為2.0,1.0,1.0。
我們發現只有特徵1，特徵2被轉換了，特徵0沒有被轉換。這是因為特徵0有6中取值（2，3，4，5，8，9），多於前面的設定setMaxCategories(5)
，因此被視為連續值了，不會被轉換。
特徵1中，（4，5，6，7，9）-->(0,1,2,3,4,5)
特徵2中,  (2,7,9)-->(0,1,2)

輸出DataFrame格式說明（Row=1）：
3個特徵 特徵0，1，2      轉換前的值  
|(3,    [0,1,2],      [2.0,5.0,7.0])
3個特徵 特徵1，1，2       轉換後的值
|(3,    [0,1,2],      [2.0,1.0,1.0])|

StringIndexer

理解了前面的VectorIndexer之後，StringIndexer對資料集的label進行重新編號就很容易理解了，都是採用類似的轉換思路，看下面的例子就可以了。

//定義一個StringIndexerModel，將label轉換成indexedlabel
StringIndexerModel labelIndexerModel=new StringIndexer().
                setInputCol("label")
                .setOutputCol("indexedLabel")
                .fit(rawData);
//加labelIndexerModel加入到Pipeline中
Pipeline pipeline=new Pipeline()
                 .setStages(new PipelineStage[]
                         {labelIndexerModel,
                         featureIndexerModel,
                         dtClassifier,
                         converter});
//檢視結果
pipeline.fit(rawData).transform(rawData).select("label","indexedLabel").show(20,false);

按label出現的頻次，轉換成0～num numOfLabels-1(分類個數)，頻次最高的轉換為0，以此類推：
label=3，出現次數最多，出現了4次，轉換（編號）為0
其次是label=2，出現了3次，編號為1，以此類推
+-----+------------+
|label|indexedLabel|
+-----+------------+
|3.0  |0.0         |
|4.0  |3.0         |
|1.0  |2.0         |
|3.0  |0.0         |
|2.0  |1.0         |
|3.0  |0.0         |
|2.0  |1.0         |
|3.0  |0.0         |
|2.0  |1.0         |
|1.0  |2.0         |
+-----+------------+

在其它地方應用StringIndexer時還需要注意兩個問題：（1）StringIndexer本質上是對String型別–>index( number);如果是：數值(numeric)–>index(number),實際上是對把數值先進行了型別轉換（ cast numeric to string and then index the string values.），也就是說無論是String，還是數值，都可以重新編號（Index); （2）利用獲得的模型轉化新資料集時，可能遇到異常情況，見下面例子。

StringIndexer對String按頻次進行編號
 id | category | categoryIndex
----|----------|---------------
 0  | a        | 0.0
 1  | b        | 2.0
 2  | c        | 1.0
 3  | a        | 0.0
 4  | a        | 0.0
 5  | c        | 1.0
 如果轉換模型（關係）是基於上面資料得到的 (a,b,c)->(0.0,2.0,1.0),如果用此模型轉換category多於（a,b,c)的資料，比如多了d，e，就會遇到麻煩：
 id | category | categoryIndex
----|----------|---------------
 0  | a        | 0.0
 1  | b        | 2.0
 2  | d        | ？
 3  | e        | ？
 4  | a        | 0.0
 5  | c        | 1.0
 Spark提供了兩種處理方式：
 StringIndexerModel labelIndexerModel=new StringIndexer().
                setInputCol("label")
                .setOutputCol("indexedLabel")
                //.setHandleInvalid("error")
                .setHandleInvalid("skip")
                .fit(rawData);
 （1）預設設定，也就是.setHandleInvalid("error")：會丟擲異常
 org.apache.spark.SparkException: Unseen label: d，e
 （2）.setHandleInvalid("skip") 忽略這些label所在行的資料，正常執行，將輸出如下結果：
 id | category | categoryIndex
----|----------|---------------
 0  | a        | 0.0
 1  | b        | 2.0
 4  | a        | 0.0
 5  | c        | 1.0

IndexToString

相應的，有StringIndexer，就應該有IndexToString。在應用StringIndexer對labels進行重新編號後，帶著這些編號後的label對資料進行了訓練，並接著對其他資料進行了預測，得到預測結果，預測結果的label也是重新編號過的，因此需要轉換回來。見下面例子，轉換回來的convetedPrediction才和原始的label對應。

         Symmetrically to StringIndexer, IndexToString maps a column of label indices back to a column containing the original labels as strings. A common use case is to produce indices from labels with StringIndexer, train a model with those indices and retrieve the original labels from the column of predicted indices with IndexToString.

IndexToString converter=new IndexToString()
                .setInputCol("prediction")//Spark預設預測label行
                .setOutputCol("convetedPrediction")//轉換回來的預測label
                .setLabels(labelIndexerModel.labels());//需要指定前面建好相互相互模型
Pipeline pipeline=new Pipeline()
                 .setStages(new PipelineStage[]
                         {labelIndexerModel,
                         featureIndexerModel,
                         dtClassifier,
                         converter});
pipeline.fit(rawData).transform(rawData)
        .select("label","prediction","convetedPrediction").show(20,false);  
|label|prediction|convetedPrediction|
+-----+----------+------------------+
|3.0  |0.0       |3.0               |
|4.0  |1.0       |2.0               |
|1.0  |2.0       |1.0               |
|3.0  |0.0       |3.0               |
|2.0  |1.0       |2.0               |
|3.0  |0.0       |3.0               |
|2.0  |1.0       |2.0               |
|3.0  |0.0       |3.0               |
|2.0  |1.0       |2.0               |
|1.0  |2.0       |1.0               |
+-----+----------+------------------+

Spark MLlib中樹剪枝方法與決策樹引數設定

**剪枝的引數設定：** 先（預）剪枝方法，通過提前停止樹的構建，而對樹進行“剪枝”：通過設定如下的條件，進行剪枝：

maxDepth：限定決策樹的最大可能深度。但由於其它終止條件或者是被剪枝的緣故，最終的決策樹的深度可能要比maxDepth小。
minInfoGain:最小資訊增益（設定閾值），小於該值將不帶繼續分叉;
minInstancesPerNode：如果某個節點的樣本數量小於該值，則該節點將不再被分叉。（設定閾值）
實際上要想獲得一個適當的閾值是相當困難的。高閾值可能導致過分簡化的樹，而低閾值可能簡化不夠。
預剪枝方法minInfoGain、minInstancesPerNode實際上是通過不斷修改停止條件來得到合理的結果，這並不是一個好辦法，事實上，我們常常甚至不知道要尋找什麼樣的結果。這樣就需要對樹進行後剪枝了（後剪枝不需要使用者指定引數，是更為理想化的剪枝方法）
Spark MLLib中用了後剪枝方法沒有？目前我還沒研究明白。
當然後剪枝方法也不總是比先剪枝方法更有效。為了尋找最佳的模型，更合理的做法是：同時使用這兩種剪技術。

DecisionTreeClassifier dtClassifier=new DecisionTreeClassifier()
            .setLabelCol("indexedLabel")
            .setFeaturesCol("indexedFeatures")
            .setMaxDepth(maxDepth)
            //.setMinInfoGain(0.5)
            //.setMinInstancesPerNode(10)
            //.setImpurity("gini")//Gini不純度
            .setImpurity("entropy")//或者熵

    The node depth is equal to the maxDepth training parameter.
     No split candidate leads to an information gain greater than minInfoGain.
     No split candidate produces child nodes which each have at least minInstancesPerNode training instances.

節點不純度和資訊增益方法設定：
分類問題可設定：
.setImpurity(“gini”)//Gini不純度
.setImpurity(“entropy”)//或者熵
這裡寫圖片描述

分類結果評估

（1）手工探索：可以簡單設定一個迴圈，對關鍵引數MaxDepth，兩種不純度不同組合計算準確度，accuracy。
（2）利用CrossValiator交叉驗證方法，可參考本人另一篇文章：
Spark2.0基於Pipeline、交叉驗證、ParamMap的模型選擇和超引數調優
http://blog.csdn.net/qq_34531825/article/details/52334436
（3）兩類的分類問題的除accuracy外的其他評價方法（指標），可參考本人另外一篇文章：
Logistic迴歸引數設定，分類結果評估（Spark2.0、Python Scikit）
http://blog.csdn.net/qq_34531825/article/details/52313553

Spark2.0決策樹分類問題完整程式碼

這裡寫程式碼片

package my.spark.ml.practice;
import org.apache.log4j.Level;
import org.apache.log4j.Logger;
import org.apache.spark.ml.Pipeline;
import org.apache.spark.ml.PipelineModel;
import org.apache.spark.ml.PipelineStage;
import org.apache.spark.ml.classification.DecisionTreeClassificationModel;
import org.apache.spark.ml.classification.DecisionTreeClassifier;
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator;
import org.apache.spark.ml.feature.IndexToString;
import org.apache.spark.ml.feature.StringIndexer;
import org.apache.spark.ml.feature.StringIndexerModel;
import org.apache.spark.ml.feature.VectorIndexer;
import org.apache.spark.ml.feature.VectorIndexerModel;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
import org.apache.spark.sql.SparkSession;

public class myDecisionTreeClassifer {

public static void main(String[] args) {
    SparkSession spark=SparkSession
                       .builder()
                       .master("local[4]")
                       .appName("myDecisonTreeClassifer")
                       .getOrCreate();
    //遮蔽日誌
      Logger.getLogger("org.apache.spark").setLevel(Level.WARN);
      Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF); 
    //-------------------0 載入資料------------------------------------------
    String path="/home/hadoop/spark/spark-2.0.0-bin-hadoop2.6" +
              "/data/mllib/sample_multiclass_classification_data.txt";
            //"/data/mllib/sample_libsvm_data.txt";
    Dataset<Row> rawData=spark.read().format("libsvm").load(path);
    Dataset<Row>[] split=rawData.randomSplit(new double[]{0.8,0.2});
    Dataset<Row> training=split[0];
    Dataset<Row> test=split[1];     

    //rawData.show(100);//載入資料檢查，顯示100行數，每一行都不截斷
    //-------------------1 建立決策樹訓練的Pipeline-------------------------------
    //1.1 對label進行重新編號
    StringIndexerModel labelIndexerModel=new StringIndexer().
            setInputCol("label")
            .setOutputCol("indexedLabel")
            //.setHandleInvalid("error")
            .setHandleInvalid("skip")
            .fit(rawData);
    //1.2 對特徵向量進行重新編號
    // Automatically identify categorical features, and index them.
    // Set maxCategories so features with > 5 distinct values are 
    //treated as continuous.
    //針對離散型特徵而言的，對離散型特徵值進行編號。
    //.setMaxCategories(5)表示假如特徵值的取值多於四種，則視為連續值
    //也就是這樣設定就無效了
    VectorIndexerModel featureIndexerModel=new VectorIndexer()
             .setInputCol("features")
             .setMaxCategories(5)
             .setOutputCol("indexedFeatures")
             .fit(rawData);
    //1.3 決策樹分類器
    /*DecisionTreeClassifier dtClassifier=
            new DecisionTreeClassifier()
            .setLabelCol("indexedLabel")//使用index後的label
            .setFeaturesCol("indexedFeatures");//使用index後的features
            */
    //1.3 決策樹分類器引數設定
    for(int maxDepth=2;maxDepth<10;maxDepth++){
        DecisionTreeClassifier dtClassifier=new DecisionTreeClassifier()
        .setLabelCol("indexedLabel")
        .setFeaturesCol("indexedFeatures")
        .setMaxDepth(maxDepth)
        //.setMinInfoGain(0.5)
        //.setMinInstancesPerNode(10)
        //.setImpurity("gini")//Gini不純度
        .setImpurity("entropy")//或者熵
        //.setMaxBins(100）//其它可除錯的還有一些引數
        ;

        //1.4 將編號後的預測label轉換回來
    IndexToString converter=new IndexToString()
            .setInputCol("prediction")//自動產生的預測label行名字
            .setOutputCol("convetedPrediction")
            .setLabels(labelIndexerModel.labels());
    //Pileline這四個階段，
    Pipeline pipeline=new Pipeline()
             .setStages(new PipelineStage[]
                     {labelIndexerModel,
                     featureIndexerModel,
                     dtClassifier,
                     converter});
    //在訓練集上訓練pipeline模型
    PipelineModel pipelineModel=pipeline.fit(training);
    //-----------------------------3 多分類結果評估----------------------------
    //預測
    Dataset<Row> testPrediction=pipelineModel.transform(test);
    MulticlassClassificationEvaluator evaluator=
            new MulticlassClassificationEvaluator()
                .setLabelCol("indexedLabel")
                .setPredictionCol("prediction")
                .setMetricName("accuracy");
    //評估
    System.out.println("MaxDepth is: "+maxDepth);
    double accuracy= evaluator.evaluate(testPrediction);
    System.out.println("accuracy is: "+accuracy);
    //輸出決策樹模型
    DecisionTreeClassificationModel treeModel =
              (DecisionTreeClassificationModel) (pipelineModel.stages()[2]);
    System.out.println("Learned classification tree model depth"
                    +treeModel.depth()+" numNodes "+treeModel.numNodes());
              //+ treeModel.toDebugString());   //輸出整個決策樹規則集    
    }//maxDepth迴圈                   
}

}

評估分類模型在測試集上的表現：
entropy:
MaxDepth is: 2
accuracy is: 0.896551724137931
Learned classification tree model depth2 numNodes 5
MaxDepth is: 3
accuracy is: 0.9310344827586207
Learned classification tree model depth3 numNodes 7
MaxDepth is: 4
accuracy is: 0.9310344827586207
Learned classification tree model depth4 numNodes 9
MaxDepth is: 5
accuracy is: 0.9310344827586207
Learned classification tree model depth5 numNodes 11
MaxDepth is: 6
accuracy is: 0.9310344827586207
Learned classification tree model depth5 numNodes 11

Gini:
MaxDepth is: 2
accuracy is: 0.8928571428571429
Learned classification tree model depth2 numNodes 5
MaxDepth is: 3
accuracy is: 0.9642857142857143
Learned classification tree model depth3 numNodes 9
MaxDepth is: 4
accuracy is: 0.9285714285714286
Learned classification tree model depth4 numNodes 13
MaxDepth is: 5
accuracy is: 0.9285714285714286
Learned classification tree model depth4 numNodes 13
MaxDepth is: 6
accuracy is: 0.9285714285714286
Learned classification tree model depth4 numNodes 13

另外：treeModel.toDebugString()將獲得類似下面的規則集：
MaxDepth is: 3
accuracy is: 0.9666666666666667
Learned classification tree model depthDecisionTreeClassificationModel 
(uid=dtc_62e3aea12022) of depth 3 with 9 nodes
  If (feature 2 <= -0.694915)
   Predict: 0.0
  Else (feature 2 > -0.694915)
   If (feature 3 <= 0.25)
    If (feature 2 <= 0.322034)
     Predict: 2.0
    Else (feature 2 > 0.322034)
     Predict: 1.0
   Else (feature 3 > 0.25)
    If (feature 2 <= 0.288136)
     Predict: 1.0
    Else (feature 2 > 0.288136)
     Predict: 1.0

結論：

提高樹的深度一般可以得到更精確的模型，但是深度越大，模型越複雜，對訓練資料集的過擬合程度越嚴重。
兩種不純度方法對效能的差異影響
（上述結論參考了《Spark機器學習》 Machine Learning with Spark一書，113頁）

本文參考了以下部落格：

其它演算法

後剪枝有多種計算方法，這裡分析一種比較簡單的演算法：
虛擬碼：

基於已有的樹切分測試資料集：
    如果存在任一子集是一棵樹，則在該子集遞迴剪枝過程
    計算將當前兩個葉節點合併後的誤差（1）
    計算不合並的誤差
    如果合併後會降低誤差的話，就將葉節點合併

這裡（1）所說的誤差是：計算每條資料的值與均值的差的平方，最後其求和,即平
方誤差的總值。這個值是混亂程度的一種表示方法。越混亂，值應該越大。所以誤
差的降低，就變得更“純”了，所以“如果合併後會降低誤差的話，就將葉節點合併”。

Spark2.0機器學習系列之3：決策樹及Spark 2.0-MLlib、Scikit程式碼分析

概述

決策樹演算法種類

Scikit中的決策樹

Spark MLlib決策樹程式碼詳細分析

VectorIndexer

StringIndexer

IndexToString

Spark MLlib中樹剪枝方法與決策樹引數設定

分類結果評估

Spark2.0決策樹分類問題完整程式碼

本文參考了以下部落格：

其它演算法

Spark2.0機器學習系列之3：決策樹及Spark 2.0-MLlib、Scikit程式碼分析

Spark2.0機器學習系列之7： MLPC（多層神經網絡）

Spark2.0機器學習系列之11：聚類(冪迭代聚類， power iteration clustering， PIC)

Spark2.0機器學習系列之10：聚類(高斯混合模型 GMM）

Spark2.0機器學習系列之1：基於Pipeline、交叉驗證、ParamMap的模型選擇和超引數調優

Spark2.0機器學習系列之2：Logistic迴歸及Binary分類（二分問題）結果評估

Spark機器學習系列之13：支援向量機SVM

機器學習入門之四：機器學習的方法-神經網絡（轉載）

機器學習系列之偏差、方差與交叉驗證

機器學習系列之特徵工程

機器學習系列之交叉驗證、網格搜尋

機器學習系列之GBDT

Python 機器學習系列之線性迴歸篇深度詳細

Java從0開始學習系列之路(6)

機器學習之二：決策樹

機器學習與深度學習系列連載：第一部分機器學習（十一）決策樹2（Decision Tree）

機器學習系列之coursera week 10 Large Scale Machine Learning

《機器學習系列教程》：第二章機器學習基礎

C#會重蹈覆轍嗎？系列之3：事件背後的臃腫設計哲學

C#基礎拾遺系列之二：使用ILSpy探索C#7.0新增功能點

Spark2.0機器學習系列之3：決策樹及Spark 2.0-MLlib、Scikit程式碼分析

概述

決策樹演算法種類

Scikit中的決策樹

Spark MLlib決策樹程式碼詳細分析

VectorIndexer

StringIndexer

IndexToString

Spark MLlib中樹剪枝方法與決策樹引數設定

分類結果評估

Spark2.0決策樹分類問題完整程式碼

本文參考了以下部落格：

其它演算法

相關推薦