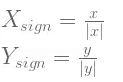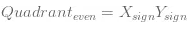七種常用特徵工程技術
應用機器學習像是把你當一個偉大的工程師,而非偉大的機器學習專家。 ---google
當在做資料探勘和資料分析時,資料是所有問題的基礎,並且會影響整個工程的流程。相比一些複雜的演算法,如何靈活的處理好資料經常會取到意想不到的效益。而處理資料不可或缺的需要使用到特徵工程。
一、什麼是特徵工程
簡單的說,特徵工程是能夠將資料像藝術一樣展現的技術。為什麼這麼說呢?因為好的特徵工程很好的混合了專業領域知識、直覺和基本的數學能力。但是最有效的資料呈現其實並不涉及任何的資料運算。
本質上來說,呈現給演算法的資料應該能擁有基本資料的相關結構或屬性。當你做特徵工程時,其實是將資料屬性轉換為資料特徵的過程,屬性代表了資料的所有維度,在資料建模時,如果對原始資料的所有屬性進行學習,並不能很好的找到資料的潛在趨勢,而通過特徵工程對你的資料進行預處理的話,你的演算法模型能夠減少受到噪聲的干擾,這樣能夠更好的找出趨勢。事實上,好的特徵甚至能夠幫你實現使用簡單的模型達到很好的效果。
但是對於特徵工程中引用的新特徵,需要驗證它確實提高的預測的準確度,而不是加入了一個無用的特徵,不然只會增加演算法運算的複雜度。
本文只提供一些簡單的特徵工程技巧,希望能夠在你以後的分析中提供幫忙。
二、常用方法
1. 表示時間戳
時間戳屬性通常需要分離成多個維度比如年、月、日、小時、分鐘、秒鐘。但是在很多的應用中,大量的資訊是不需要的。比如在一個監督系統中,嘗試利用一個’位置+時間‘的函式預測一個城市的交通故障程度,這個例項中,大部分會受到誤導只通過不同的秒數去學習趨勢,其實是不合理的。並且維度'年'也不能很好的給模型增加值的變化,我們可能僅僅需要小時、日、月等維度。因此當我們在呈現時間的時候,試著保證你所提供的所有資料是你的模型所需要的。
並且別忘了時區,假如你的資料來源來自不同的地理資料來源,別忘了利用時區將資料標準化。
2. 分解類別屬性
一些屬性是類別型而不是數值型,舉一個簡單的例子,由{紅,綠、藍}組成的顏色屬性,最常用的方式是把每個類別屬性轉換成二元屬性,即從{0,1}取一個值。因此基本上增加的屬性等於相應數目的類別,並且對於你資料集中的每個例項,只有一個是1(其他的為0),這也就是獨熱(one-hot)編碼方式(類似於轉換成啞變數)。
如果你不瞭解這個編碼的話,你可能會覺得分解會增加沒必要的麻煩(因為編碼大量的增加了資料集的維度)。相反,你可能會嘗試將類別屬性轉換成一個標量值,例如顏色屬性可能會用{1,2,3}表示{紅,綠,藍}。這裡存在兩個問題,首先,對於一個數學模型,這意味著某種意義上紅色和綠色比和藍色更“相似”(因為|1-3| > |1-2|)。除非你的類別擁有排序的屬性(比如鐵路線上的站),這樣可能會誤導你的模型。然後,可能會導致統計指標(比如均值)無意義,更糟糕的情況是,會誤導你的模型。還是顏色的例子,假如你的資料集包含相同數量的紅色和藍色的例項,但是沒有綠色的,那麼顏色的均值可能還是得到2,也就是綠色的意思。
能夠將類別屬性轉換成一個標量,最有效的場景應該就是隻有兩個類別的情況。即{0,1}對應{類別1,類別2}。這種情況下,並不需要排序,並且你可以將屬性的值理解成屬於類別1或類別2的概率。
3.分箱/分割槽
有時候,將數值型屬性轉換成類別呈現更有意義,同時能使演算法減少噪聲的干擾,通過將一定範圍內的數值劃分成確定的塊。舉個例子,我們預測一個人是否擁有某款衣服,這裡年齡是一個確切的因子。其實年齡組是更為相關的因子,所有我們可以將年齡分佈劃分成1-10,11-18,19-25,26-40等。而且,不是將這些類別分解成2個點,你可以使用標量值,因為相近的年齡組表現出相似的屬性。
只有在瞭解屬性的領域知識的基礎,確定屬效能夠劃分成簡潔的範圍時分割槽才有意義。即所有的數值落入一個分割槽時能夠呈現出共同的特徵。在實際應用中,當你不想讓你的模型總是嘗試區分值之間是否太近時,分割槽能夠避免出現過擬合。例如,如果你所感興趣的是將一個城市作為整體,這時你可以將所有落入該城市的維度值進行整合成一個整體。分箱也能減小小錯誤的影響,通過將一個給定值劃入到最近的塊中。如果劃分範圍的數量和所有可能值相近,或對你來說準確率很重要的話,此時分箱就不適合了。
4. 特徵交叉
特徵交叉算是特徵工程中非常重要的方法之一了,特徵交叉是一種很獨特的方式,它將兩個或更多的類別屬性組合成一個。當組合的特徵要比單個特徵更好時,這是一項非常有用的技術。數學上來說,是對類別特徵的所有可能值進行交叉相乘。
假如擁有一個特徵A,A有兩個可能值{A1,A2}。擁有一個特徵B,存在{B1,B2}等可能值。然後,A&B之間的交叉特徵如下:{(A1,B1),(A1,B2),(A2,B1),(A2,B2)},並且你可以給這些組合特徵取任何名字。但是需要明白每個組合特徵其實代表著A和B各自資訊協同作用。
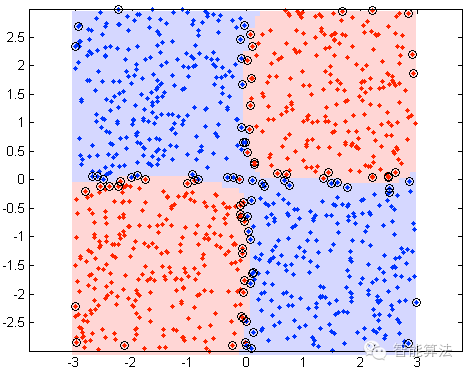
舉個栗子,如下圖中:
所有的藍色點屬於一類,紅色屬於另外一類。我們不考慮實際模型,首先,將X,Y值分成{x<0,x>=0}&{y<0,y>=0}對我們來說會很有用,將劃分結果取名為{Xn,Xp}和{Yn,Yp}。很顯然I&III象限對應於紅色類別,II&IV象限是藍色類。因此如果現在將特徵X和特徵Y組成成交叉特徵,你會有四個象限特徵,{I,II,III,IV}分別對應於{(Xp, Yp), (Xn, Yp), (Xn, Yn), (Xp, Yn)} 。
一個更好地詮釋好的交叉特徵的例項是類似於(經度,緯度)。一個相同的經度對應了地圖上很多的地方,緯度也是一樣。但是一旦你將經度和緯度組合到一起,它們就代表了地理上特定的一塊區域,區域中每一部分是擁有著類似的特性。
有時候,能夠通過簡單的數學技巧將資料的屬性組合成一個單一的特徵。在上一個例子中,將更改的特徵設定為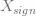
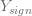
將新的特徵定義為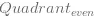
我們可以根據確定特徵如果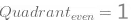
5. 特徵選擇
為了得到更好的模型,使用某些演算法自動的選出原始特徵的子集。這個過程,你不會構建或修改你擁有的特徵,但是會通過修剪特徵來達到減少噪聲和冗餘。
那些和我們解決的問題無關需要被移除的屬性,在我們的資料特徵中存在了一些特徵對於提高模型的準確率比其他更重要的特徵,也還有一些特徵與其他特徵放在一起出現了冗餘,特徵選擇是通過自動選出對於解決問題最有用的特徵子集來解決上述問題的。
特徵選擇演算法可能會用到評分方法來排名和選擇特徵,比如相關性或其他確定特徵重要性的方法,更進一步的方法可能需要通過試錯,來搜尋出特徵子集。
還有通過構建輔助模型的方法,逐步迴歸就是模型構造過程中自動執行特徵選擇演算法的一個例項,還有像Lasso迴歸和嶺迴歸等正則化方法也被歸入到特徵選擇,通過加入額外的約束或者懲罰項加到已有模型(損失函式)上,以防止過擬合併提高泛化能力。
6. 特徵縮放
有時候,你可能會注意到某些特徵比其他特徵擁有高得多的跨度值。舉個例子,將一個人的收入和他的年齡進行比較,更具體的例子,如某些模型(像嶺迴歸)要求你必須將特徵值縮放到相同的範圍值內。通過縮放可以避免某些特徵比其他特徵獲得大小非常懸殊的權重值。
7. 特徵提取
特徵提取涉及到從原始屬性中自動生成一些新的特徵集的一系列演算法,降維演算法就屬於這一類。特徵提取是一個自動將觀測值降維到一個足夠建模的小資料集的過程。對於列表資料,可使用的方法包括一些投影方法,像主成分分析和無監督聚類演算法。對於圖形資料,可能包括一些直線檢測和邊緣檢測,對於不同領域有各自的方法。
特徵提取的關鍵點在於這些方法是自動的(雖然可能需要從簡單方法中設計和構建得到),還能夠解決不受控制的高維資料的問題。大部分的情況下,是將這些不同型別資料(如圖,語言,視訊等)存成數字格式來進行模擬觀察。
免責宣告:本文系網路轉載。版權歸原作者所有。如涉及版權,請聯絡刪除!