大家貌似都叫Recurrent Neural Networks為迴圈神經網路。

我之前是查維基百科的緣故，所以一直叫它遞迴網路。

遞迴神經網路（RNN）是兩種人工神經網路的總稱。一種是時間遞迴神經網路（recurrent neural network），另一種是結構遞迴神經網路（recursive neural network）。

下面我所提到的遞迴網路全部都是指Recurrent Neural Networks。

遞迴神經網路的討論分為三部分

1. 介紹：描述遞迴網路和前饋網路的差別和優劣
   
2. 實現：梯度消失和梯度爆炸問題，及解決問題的LSTM和GRU
   
3. 程式碼：用tensorflow實際演示一個任務的訓練和使用
   

該文為第一部分：

文中有很多動態圖，請點選觀看，看不了的話建議去上面的gitbook地址閱讀

遞迴神經網路——介紹

時序預測問題

程式碼演示3已經展示瞭如何用前饋神經網路（feedforward）來做時序訊號預測。

一、用前饋神經網路來做時序訊號預測有什麼問題？

• 依賴受限：前饋網路是利用窗處理將不同時刻的向量並接成一個更大的向量。以此利用前後發生的事情預測當前所發生的情況。如下圖所示：
  

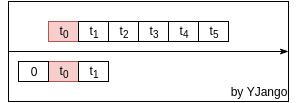
  但其所能考慮到的前後依賴受限於將多少個向量（window size）並接在一起。所能考慮的依賴始終是固定長度的。

• 網路規格：想要更好的預測，需要讓網路考慮更多的前後依賴。

  例：若僅給“國（）”，讓玩家猜括號中的字時，所能想到的可能性非常之多。但若給“中國（）”時，可能性範圍降低。當給“我是中國（）”時，猜中的可能性會進一步增加。

  那麼很自然的做法就是擴大並接向量的數量，但這樣做的同時也會使輸入向量的維度和神經網路第一層的權重矩陣的大小快速增加。如程式碼演示3中每個輸入向量的維度是39，41幀的窗處理之後，維度變成了1599，並且神經網路第一層的權重矩陣也變成了1599 by n（n為下一層的節點數）。其中很多權重都是冗餘的，但卻不得不一直存在於每一次的預測之中。

• 訓練所需樣本數：前兩點可能無傷大雅，而真正使得遞迴神經網路（recurrent）在時序預測中擊敗前饋神經網路的關鍵在於訓練網路所需要的資料量。

網路差異之處

幾乎所有的神經網路都可以看作為一種特殊制定的前饋神經網路，這裡“特殊制定”的作用在於縮減尋找對映函式的搜尋空間，也正是因為搜尋空間的縮小，才使得網路可以用相對較少的資料量學習到更好的規律。

例：解一元二次方程。我們需要兩組配對的來解該方程。但是如果我們知道實際上是，這時就只需要一對就可以確定與的關係。遞迴神經網路和卷積神經網路等神經網路的變體就具有類似的功效。

二、相比前饋神經網路，遞迴神經網路究竟有何不同之處？

需要注意的是遞迴網路並非只有一種結構，這裡介紹一種最為常用和有效的遞迴網路結構。

數學視角

首先讓我們用從輸入層到隱藏層的空間變換視角來觀察，不同的地方在於，這次將時間維度一起考慮在內。

注：這裡的圓圈不再代表節點，而是狀態，是輸入向量和輸入經過隱藏層後的向量。

前饋網路：window size為3幀的窗處理後的前饋網路

• 動態圖：左側是時間維度展開前，右側是展開後（單位時刻實際工作的只有灰色部分。）。前饋網路的特點使不同時刻的預測完全是獨立的。我們只能通過窗處理的方式讓其照顧到前後相關性。

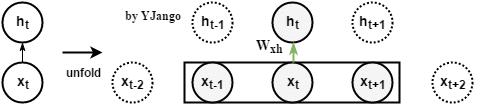
• 數學式子：，concat表示將向量並接成一個更大維度的向量。

• 學習引數：需要從大量的資料中學習和。

  要學習各個時刻（3個）下所有維度（39維）的關係（39*3個），就需要很多資料。

遞迴網路：不再有window size的概念，而是time step

• 動態圖：左側是時間維度展開前，迴路方式的表達方式，其中黑方框表示時間延遲。右側展開後，可以看到當前時刻的並不僅僅取決於當前時刻的輸入，同時與上一時刻的也相關。

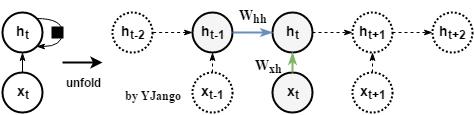
• 數學式子：。同樣也由經的變化後的資訊決定，

  但這裡多另一份資訊：，而該資訊是從上一時刻的隱藏狀態經過一個不同的變換後得出的。

  注：的形狀是行為dim_input，列為dim_hidden_state，而是一個行列都為dim_hidden_state的方陣。

• 學習引數：前饋網路需要3個時刻來幫助學習一次，而遞迴網路可以用3個時刻來幫助學習3次和。換句話說：所有時刻的權重矩陣都是共享的。這是遞迴網路相對於前饋網路而言最為突出的優勢。

遞迴神經網路是在時間結構上存在共享特性的神經網路變體。

時間結構共享是遞迴網路的核心中的核心。

物理視角

共享特性給網路帶來了諸多好處，但也產生了另一個問題：

三、為什麼可以共享？

在物理視角中，YJango想給大家展示的第一點就是為什麼我們可以用這種共享不同時刻權重矩陣的網路進行時序預測。

下圖可以從直覺上幫助大家感受日常生活中很多時序訊號是如何產生的。

• 例1：軌跡的產生，如地球的軌跡有兩條線索決定，其中一條是地球自轉，另一條是地球圍繞太陽的公轉。下圖是太陽和其他星球。自轉相當於，而公轉相當於。二者共同決定實際軌跡。

• 例2：同理萬花尺

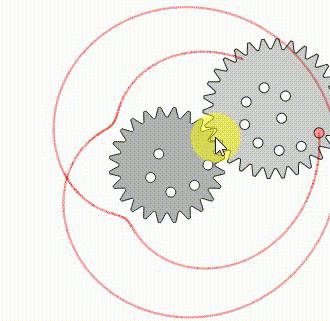
• 例3：演奏音樂時，樂器將力轉成相應的震動產生聲音，而整個演奏擁有一個主旋律貫穿全曲。其中樂器的物理特性就相當於，同一樂器在各個時刻物理特性在各個時刻都是共享的。其內在也有一個隱藏的主旋律基準，旋律資訊與音樂資訊共同決定下一時刻的實際聲音。

上述例子中所產生的軌跡、音樂都是我們所能觀察到的observations，我們常常會利用這些observation作為依據來做出決策。

下面的例子可能更容易體會共享特性對於資料量的影響。

• 例項：捏陶瓷：不同角度相當於不同的時刻

• 若用前饋網路：網路訓練過程相當於不用轉盤，而是徒手將各個角度捏成想要的形狀。不僅工作量大，效果也難以保證。

• 若用遞迴網路：網路訓練過程相當於在不斷旋轉的轉盤上，以一種手勢捏造所有角度。工作量降低，效果也可保證。

遞迴網路特點

• 時序長短可變：只要知道上一時刻的隱藏狀態與當前時刻的輸入，就可以計算當前時刻的隱藏狀態。並且由於計算所用到的與在任意時刻都是共享的。遞迴網路可以處理任意長度的時間序列。

• 顧及時間依賴：若當前時刻是第5幀的時序訊號，那計算當前的隱藏狀態就需要當前的輸入和第4幀的隱藏狀態，而計算又需要，這樣不斷逆推到初始時刻為止。意味著常規遞迴網路對過去所有狀態都存在著依賴關係。

  注：在計算的值時，若沒有特別指定初始隱藏狀態，則會將全部補零，

  表示式會變成前饋神經網路：

• 未來資訊依賴：前饋網路是通過並接未來時刻的向量來引入未來資訊對當前內容判斷的限制，但常規的遞迴網路只對所有過去狀態存在依賴關係。所以遞迴網路的一個擴充套件就是雙向（bidirectional）遞迴網路：兩個不同方向的遞迴層疊加。

  • 關係圖：正向（forward）遞迴層是從最初時刻開始，而反向（backward）遞迴層是從最末時刻開始。

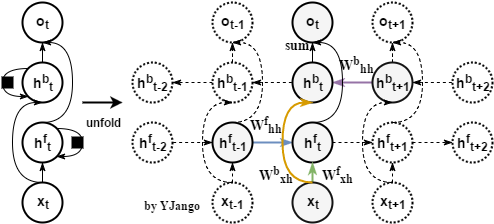
  • 數學式子：

    • 正向遞迴層：
    • 反向遞迴層：
      

    • 雙向遞迴層：

      注：還有並接的處理方式，即，但反向遞迴層的作用是引入未來資訊對當前預測判斷的額外限制。並不是資訊維度不夠。至少在我所有的實驗中，相加（sum）的方式往往優於並接。

      注：也有人將正向遞迴層和反向遞迴層中的權重與共享，與共享。我沒有做實驗比較過。但直覺上與共享在某些任務中可能會有些許提升。與的共享恐怕並不會起到什麼作用（要貼合任務而言）。

      注：隱藏狀態通常不會是網路的最終結果，一般都會將再接著另一個將其投射到輸出狀態。一個最基本的遞迴網路不會出現前饋神經網路那樣從輸入層直接到輸出層的情況，而是至少會有一個隱藏層。

      注：雙向遞迴層可以提供更好的識別預測效果，但卻不能實時預測，由於反向遞迴的計算需要從最末時刻開始，網路不得不等待著完整序列都產生後才可以開始預測。在對於實時識別有要求的線上語音識別，其應用受限。

  
  

• 遞迴網路輸出：遞迴網路的出現實際上是對前饋網路在時間維度上的擴充套件。

  • 關係圖：常規網路可以將輸入和輸出以向量對向量（無時間維度）的方式進行關聯。而遞迴層的引入將其擴充套件到了序列對序列的匹配。從而產生了one to one右側的一系列關聯方式。較為特殊的是最後一個many to many，發生在輸入輸出的序列長度不確定時，其實質兩個遞迴網路的拼接使用，公共點在紫色的隱藏狀態。

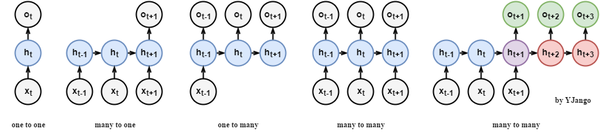
    • many to one：常用在情感分析中，將一句話關聯到一個情感向量上去。
    • many to many：第一個many to many在DNN-HMM語音識別框架中常有用到
    • many to many(variable length)：第二個many to many常用在機器翻譯兩個不同語言時。

• 遞迴網路資料：遞迴網路由於引入time step的緣故，使得其訓練資料與前饋網路有所不同。

  • 前饋網路：輸入和輸出：矩陣

    輸入矩陣形狀：(n_samples, dim_input)

    輸出矩陣形狀：(n_samples, dim_output)

    注：真正測試/訓練的時候，網路的輸入和輸出就是向量而已。加入n_samples這個維度是為了可以實現一次訓練多個樣本，求出平均梯度來更新權重，這個叫做Mini-batch gradient descent。

    如果n_samples等於1，那麼這種更新方式叫做Stochastic Gradient Descent (SGD)。

  • 遞迴網路：輸入和輸出：維度至少是3的張量，如果是圖片等資訊，則張量維度仍會增加。

    輸入張量形狀：(time_steps, n_samples, dim_input)

    輸出張量形狀：(time_steps, n_samples, dim_output)

    注：同樣是保留了Mini-batch gradient descent的訓練方式，但不同之處在於多了time step這個維度。

    Recurrent 的任意時刻的輸入的本質還是單個向量，只不過是將不同時刻的向量按順序輸入網路。你可能更願意理解為一串向量 a sequence of vectors，或者是矩陣。

網路對待

請以層的概念對待所有網路。遞迴神經網路是指擁有遞迴層的神經網路，其關鍵在於網路中存在遞迴層。

每一層的作用是將資料從一個空間變換到另一個空間下。可以視為特徵抓取方式，也可以視為分類器。二者沒有明顯界限並彼此包含。關鍵在於使用者如何理解。

以層的概念理解網路的好處在於，今後的神經網路往往並不會僅用到一種處理手段。往往是前饋、遞迴、卷積混合使用。 這時就無法再以遞迴神經網路來命名該結構。

例：下圖中就是在雙向遞迴層的前後分別又加入了兩個前饋隱藏層。也可以堆積更多的雙向遞迴層，人們也會在其前面加入“深層”二字，提高逼格。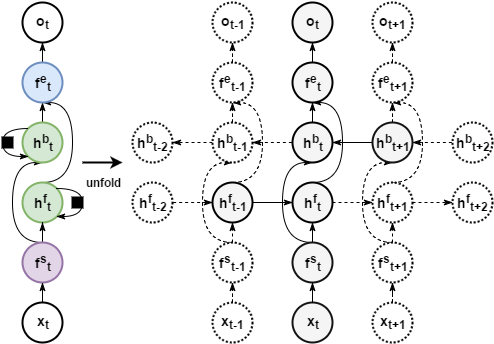

注：層並不是圖中所畫的圓圈，而是連線。圓圈所表示的是穿過各層前後的狀態。

遞迴網路問題

常規遞迴網路從理論上應該可以顧及所有過去時刻的依賴，然而實際卻無法按人們所想象工作。原因在於梯度消失（vanishinggradient）和梯度爆炸（exploding gradient）問題。下一節就是介紹Long Short Term Memory（LSTM）和Gated Recurrent Unit（GRU）：遞迴網路的特別實現演算法。