(轉載)深度學習基礎(7)——遞迴神經網路
原文地址:https://zybuluo.com/hanbingtao/note/626300
轉載在此的目的是自己做個筆記,日後好複習,如侵權請聯絡我!!
在前面的文章中,我們介紹了迴圈神經網路,它可以用來處理包含序列結構的資訊。然而,除此之外,資訊往往還存在著諸如樹結構、圖結構等更復雜的結構。對於這種複雜的結構,迴圈神經網路就無能為力了。本文介紹一種更為強大、複雜的神經網路:遞迴神經網路 (Recursive Neural Network, RNN),以及它的訓練演算法BPTS (Back Propagation Through Structure)。顧名思義,遞迴神經網路(巧合的是,它的縮寫和迴圈神經網路一樣,也是RNN)可以處理諸如樹、圖這樣的遞迴結構。在文章的最後,我們將實現一個遞迴神經網路,並介紹它的幾個應用場景。
什麼是遞迴神經網路?
因為神經網路的輸入層單元個數是固定的,因此必須用迴圈或者遞迴的方式來處理長度可變的輸入。迴圈神經網路實現了前者,通過將長度不定的輸入分割為等長度的小塊,然後再依次的輸入到網路中,從而實現了神經網路對變長輸入的處理。一個典型的例子是,當我們處理一句話的時候,我們可以把一句話看作是片語成的序列,然後,每次向迴圈神經網路輸入一個詞,如此迴圈直至整句話輸入完畢,迴圈神經網路將產生對應的輸出。如此,我們就能處理任意長度的句子了。入下圖所示:
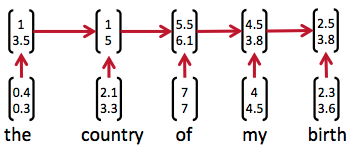
然而,有時候把句子看做是詞的序列是不夠的,比如下面這句話『兩個外語學院的學生』:
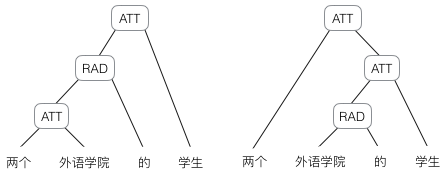
上圖顯示了這句話的兩個不同的語法解析樹。可以看出來這句話有歧義,不同的語法解析樹則對應了不同的意思。一個是『兩個外語學院的/學生』,也就是學生可能有許多,但他們來自於兩所外語學校;另一個是『兩個/外語學院的學生』,也就是隻有兩個學生,他們是外語學院的。為了能夠讓模型區分出兩個不同的意思,我們的模型必須能夠按照樹結構去處理資訊,而不是序列,這就是遞迴神經網路的作用。當面對按照樹/圖結構處理資訊更有效的任務時,遞迴神經網路通常都會獲得不錯的結果。
遞迴神經網路可以把一個樹/圖結構資訊編碼為一個向量,也就是把資訊對映到一個語義向量空間中。這個語義向量空間滿足某類性質,比如語義相似的向量距離更近。也就是說,如果兩句話(儘管內容不同)它的意思是相似的,那麼把它們分別編碼後的兩個向量的距離也相近;反之,如果兩句話的意思截然不同,那麼編碼後向量的距離則很遠。如下圖所示:
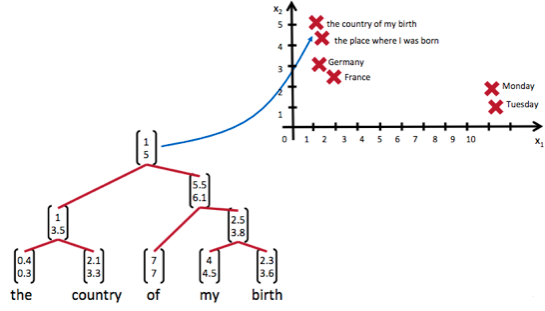
從上圖我們可以看到,遞迴神經網路將所有的詞、句都對映到一個2維向量空間中。句子『the country of my birth』和句子『the place where I was born』的意思是非常接近的,所以表示它們的兩個向量在向量空間中的距離很近。另外兩個詞『Germany』和『France』因為表示的都是地點,它們的向量與上面兩句話的向量的距離,就比另外兩個表示時間的詞『Monday』和『Tuesday』的向量的距離近得多。這樣,通過向量的距離,就得到了一種語義的表示。
上圖還顯示了自然語言可組合的性質:詞可以組成句、句可以組成段落、段落可以組成篇章,而更高層的語義取決於底層的語義以及它們的組合方式。遞迴神經網路是一種表示學習,它可以將詞、句、段、篇按照他們的語義對映到同一個向量空間中,也就是把可組合(樹/圖結構)的資訊表示為一個個有意義的向量。比如上面這個例子,遞迴神經網路把句子"the country of my birth"表示為二維向量[1,5]。有了這個『編碼器』之後,我們就可以以這些有意義的向量為基礎去完成更高階的任務(比如情感分析等)。如下圖所示,遞迴神經網路在做情感分析時,可以比較好的處理否定句,這是勝過其他一些模型的:

在上圖中,藍色表示正面評價,紅色表示負面評價。每個節點是一個向量,這個向量表達了以它為根的子樹的情感評價。比如"intelligent humor"是正面評價,而"care about cleverness wit or any other kind of intelligent humor"是中性評價。我們可以看到,模型能夠正確的處理doesn't的含義,將正面評價轉變為負面評價。
儘管遞迴神經網路具有更為強大的表示能力,但是在實際應用中並不太流行。其中一個主要原因是,遞迴神經網路的輸入是樹/圖結構,而這種結構需要花費很多人工去標註。想象一下,如果我們用迴圈神經網路處理句子,那麼我們可以直接把句子作為輸入。然而,如果我們用遞迴神經網路處理句子,我們就必須把每個句子標註為語法解析樹的形式,這無疑要花費非常大的精力。很多時候,相對於遞迴神經網路能夠帶來的效能提升,這個投入是不太划算的。
我們已經基本瞭解了遞迴神經網路是做什麼用的,接下來,我們將探討它的演算法細節。
遞迴神經網路的前向計算
接下來,我們詳細介紹一下遞迴神經網路是如何處理樹/圖結構的資訊的。在這裡,我們以處理樹型資訊為例進行介紹。
遞迴神經網路的輸入是兩個子節點(也可以是多個),輸出就是將這兩個子節點編碼後產生的父節點,父節點的維度和每個子節點是相同的。如下圖所示:
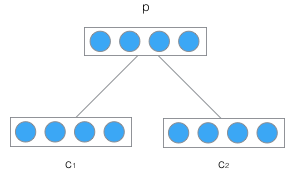
c1和c2分別表示兩個子節點的向量,p是表示父節點的向量。子節點和父節點組成的一個全連線神經網路,也就是子節點的每個神經元都和父節點的每個神經元兩兩相連。我們用矩陣W表示這些連線上的權重,他的維度將是d x 2d,其中,d表示每個節點的維度。父節點的計算公式可以寫成:
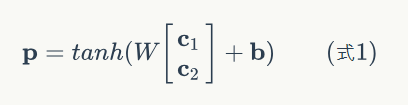
在上式中,tanh是啟用函式(當然也可以用其它的啟用函式),b是偏置項,它也是一個維度為d的向量。如果讀過前面的文章,相信大家已經非常熟悉這些計算了,在此不做過多的解釋了。
然後,我們把產生的父節點的向量和其他子節點的向量再次作為網路的輸入,再次產生它們的父節點。如此遞迴下去,直至整棵樹處理完畢。最終,我們將得到根節點的向量,我們可以認為它是對整棵樹的表示,這樣我們就實現了把樹對映為一個向量。在下圖中,我們使用遞迴神經網路處理一棵樹,最終得到的向量p3,就是對整棵樹的表示:
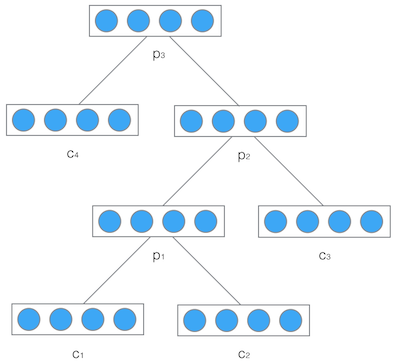
舉個例子,我們使用遞迴神經網路將{兩個外語學校的學生}對映成一個向量,如下圖:
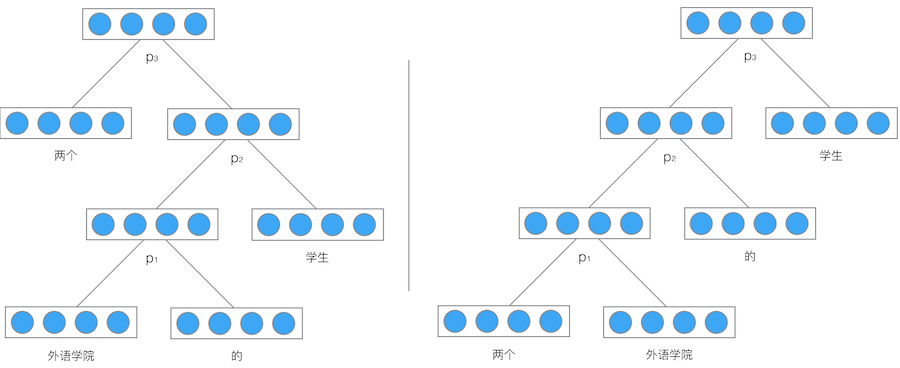
最後得到的向量p3就是對整個句子『兩個外語學校的學生』的表示。由於整個結構是遞迴的,不僅僅是根節點,事實上每個節點都是以其為根的子樹的表示。比如,在左邊的這棵樹中,向量p2是短語『外語學院的學生』的表示,而向量p1是短語『外語學院的』的表示。
式1就是遞迴神經網路的前向計算演算法。它和全連線神經網路的計算沒有什麼區別,只是在輸入的過程中需要根據輸入的樹結構依次輸入每個子節點。
需要特別注意的是,遞迴神經網路的權重W和偏置項b在所有的節點都是共享的。
遞迴神經網路的訓練
遞迴神經網路的訓練演算法和迴圈神經網路類似,兩者不同之處在於,前者需要將殘差從根節點反向傳播到各個子節點,而後者是將殘差從當前時刻tk反向傳播到初始時刻t1.。
下面我們介紹適用於遞迴神經網路的訓練演算法,也就是BPTS演算法。
誤差項的傳遞
首先,我們先推導將誤差從父節點傳遞到子節點的公式,如下圖:
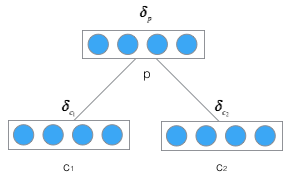




有了傳遞一層的公式,我們就不難寫出逐層傳遞的公式:
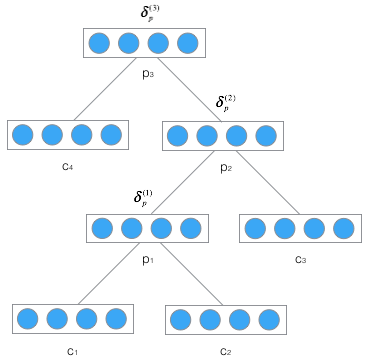

權重梯度的計算
根據加權輸入的計算公式:

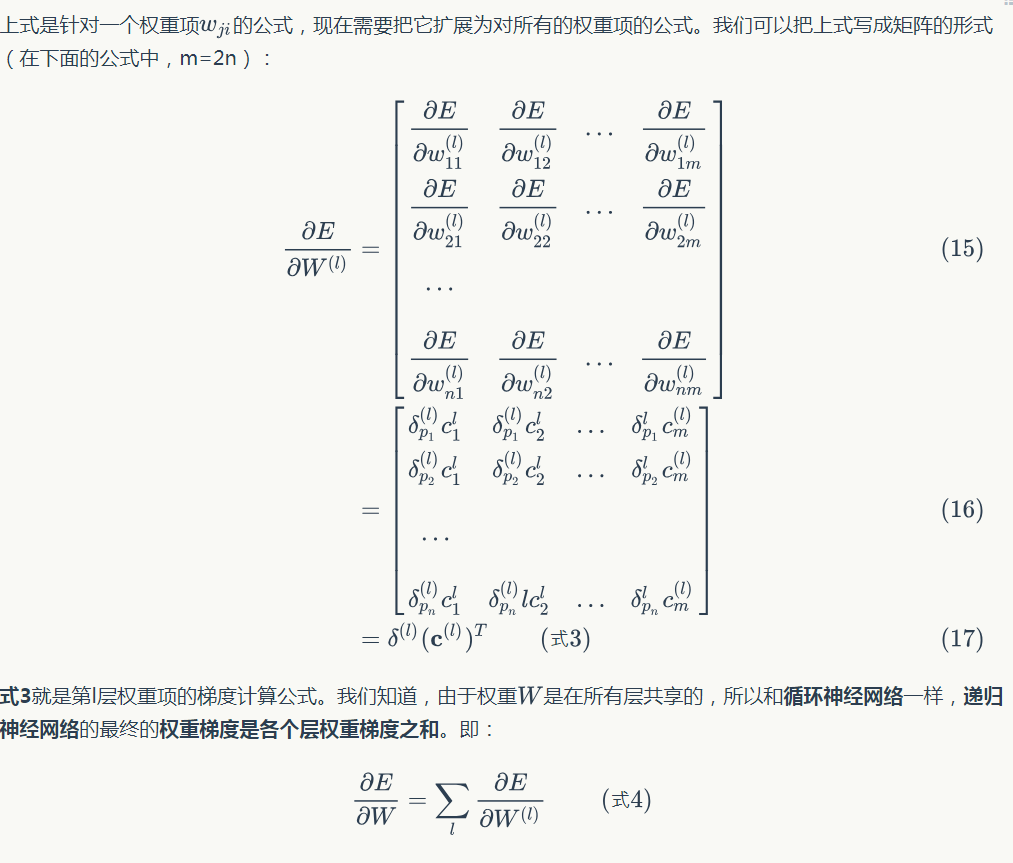
因為迴圈神經網路的證明過程已經在(轉載)深度學習基礎(4)——卷積神經網路一文中給出,因此,遞迴神經網路{為什麼最終梯度是各層梯度之和}的證明就留給讀者自行完成了。
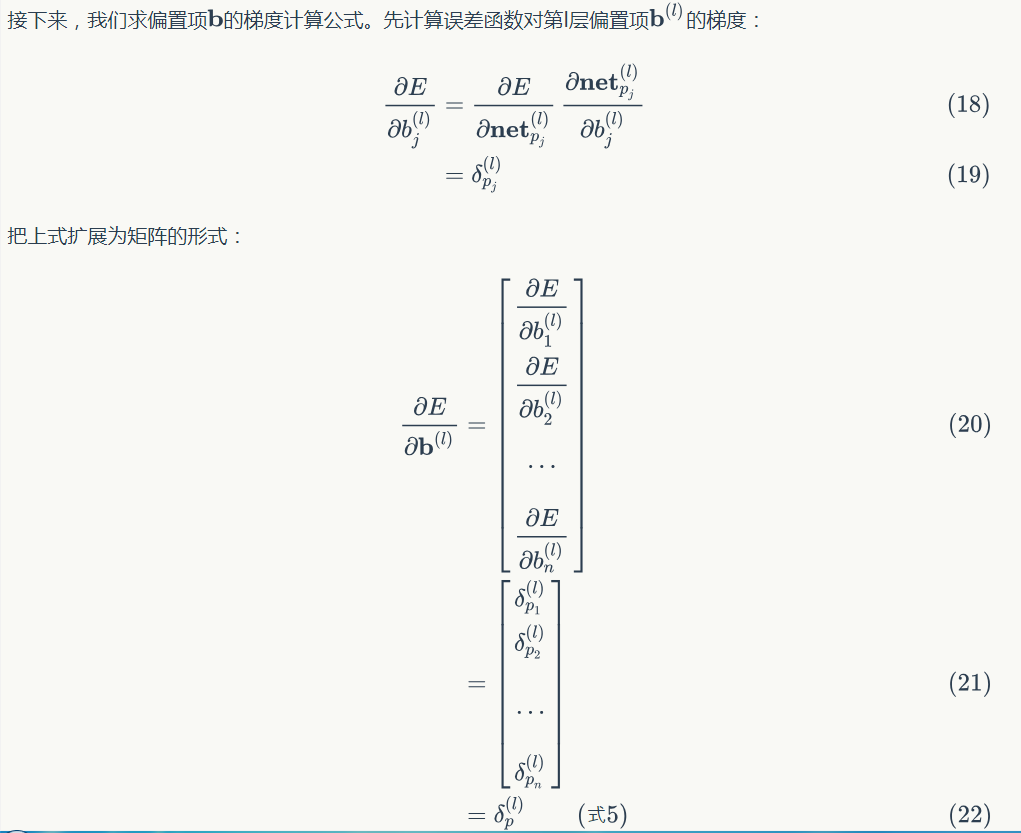

權重更新
如果使用梯度下降優化演算法,那麼權重更新公式為:
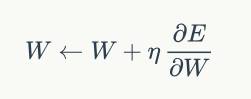
其中,ita是學習速率常數,把公式4帶到上式,即可完成權重的更新,同理,偏置項的更新公式為:
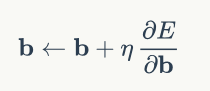
把公式6帶入到上式,即可完成偏置項的更新。
這就是遞迴神經網路的訓練演算法BPTS。由於我們有了前面幾篇文章的基礎,相信讀者們理解BPTS演算法也會比較容易。
遞迴神經網路的實現
現在,我們實現一個處理樹型結構的遞迴神經網路。
在檔案的開頭,加入如下程式碼:
#!/usr/bin/env python # -*- coding: UTF-8 -*- import numpy as np from cnn import IdentityActivator
上述四行程式碼非常簡單,沒有什麼需要解釋的。IdentityActivator啟用函式是在我們介紹卷積神經網路時寫的,現在引用一下它。
我們首先定義一個樹節點結果,這樣,我們就可以用它儲存卷積神經網路生成的整棵樹:
class TreeNode(object):
def __init__(self, data, children=[], children_data=[]):
self.parent = None
self.children = children
self.children_data = children_data
self.data = data
for child in children:
child.parent = self
接下來,我們把遞迴神經網路的實現程式碼都放在RecursiveLayer類中,下面是這個類的建構函式:
# 遞迴神經網路實現
class RecursiveLayer(object):
def __init__(self, node_width, child_count,
activator, learning_rate):
'''
遞迴神經網路建構函式
node_width: 表示每個節點的向量的維度
child_count: 每個父節點有幾個子節點
activator: 啟用函式物件
learning_rate: 梯度下降演算法學習率
'''
self.node_width = node_width
self.child_count = child_count
self.activator = activator
self.learning_rate = learning_rate
# 權重陣列W
self.W = np.random.uniform(-1e-4, 1e-4,
(node_width, node_width * child_count))
# 偏置項b
self.b = np.zeros((node_width, 1))
# 遞迴神經網路生成的樹的根節點
self.root = None
下面是前向計算的實現:
def forward(self, *children):
'''
前向計算
'''
children_data = self.concatenate(children)
parent_data = self.activator.forward(
np.dot(self.W, children_data) + self.b
)
self.root = TreeNode(parent_data, children
, children_data)
forward函式接收一系列的樹節點物件作為輸入,然後,遞迴神經網路將這些樹節點作為子節點,並計算它們的父節點。最後,將計算的父節點儲存在self.root變數中。
上面用到的concatenate函式,是將各個子節點中的資料拼接成一個長向量,其程式碼如下:
def concatenate(self, tree_nodes):
'''
將各個樹節點中的資料拼接成一個長向量
'''
concat = np.zeros((0,1))
for node in tree_nodes:
concat = np.concatenate((concat, node.data))
return concat
下面是反向傳播演算法BPTS的實現:
def backward(self, parent_delta):
'''
BPTS反向傳播演算法
'''
self.calc_delta(parent_delta, self.root)
self.W_grad, self.b_grad = self.calc_gradient(self.root)
def calc_delta(self, parent_delta, parent):
'''
計算每個節點的delta
'''
parent.delta = parent_delta
if parent.children:
# 根據式2計算每個子節點的delta
children_delta = np.dot(self.W.T, parent_delta) * (
self.activator.backward(parent.children_data)
)
# slices = [(子節點編號,子節點delta起始位置,子節點delta結束位置)]
slices = [(i, i * self.node_width,
(i + 1) * self.node_width)
for i in range(self.child_count)]
# 針對每個子節點,遞迴呼叫calc_delta函式
for s in slices:
self.calc_delta(children_delta[s[1]:s[2]],
parent.children[s[0]])
def calc_gradient(self, parent):
'''
計算每個節點權重的梯度,並將它們求和,得到最終的梯度
'''
W_grad = np.zeros((self.node_width,
self.node_width * self.child_count))
b_grad = np.zeros((self.node_width, 1))
if not parent.children:
return W_grad, b_grad
parent.W_grad = np.dot(parent.delta, parent.children_data.T)
parent.b_grad = parent.delta
W_grad += parent.W_grad
b_grad += parent.b_grad
for child in parent.children:
W, b = self.calc_gradient(child)
W_grad += W
b_grad += b
return W_grad, b_grad
在上述演算法中,calc_delta函式和calc_gradient函式分別計算各個節點的誤差項以及最終的梯度。它們都採用遞迴演算法,先序遍歷整個樹,並逐一完成每個節點的計算。
下面是梯度下降演算法的實現(沒有weight decay),這個非常簡單:
def update(self):
'''
使用SGD演算法更新權重
'''
self.W -= self.learning_rate * self.W_grad
self.b -= self.learning_rate * self.b_grad
以上就是遞迴神經網路的實現,總共100行左右,和上一篇文章的LSTM相比簡單多了。
最後,我們用梯度檢查來驗證程式的正確性:
def gradient_check():
'''
梯度檢查
'''
# 設計一個誤差函式,取所有節點輸出項之和
error_function = lambda o: o.sum()
rnn = RecursiveLayer(2, 2, IdentityActivator(), 1e-3)
# 計算forward值
x, d = data_set()
rnn.forward(x[0], x[1])
rnn.forward(rnn.root, x[2])
# 求取sensitivity map
sensitivity_array = np.ones((rnn.node_width, 1),
dtype=np.float64)
# 計算梯度
rnn.backward(sensitivity_array)
# 檢查梯度
epsilon = 10e-4
for i in range(rnn.W.shape[0]):
for j in range(rnn.W.shape[1]):
rnn.W[i,j] += epsilon
rnn.reset_state()
rnn.forward(x[0], x[1])
rnn.forward(rnn.root, x[2])
err1 = error_function(rnn.root.data)
rnn.W[i,j] -= 2*epsilon
rnn.reset_state()
rnn.forward(x[0], x[1])
rnn.forward(rnn.root, x[2])
err2 = error_function(rnn.root.data)
expect_grad = (err1 - err2) / (2 * epsilon)
rnn.W[i,j] += epsilon
print 'weights(%d,%d): expected - actural %.4e - %.4e' % (
i, j, expect_grad, rnn.W_grad[i,j])
return rnn
下面是梯度檢查的結果,完全正確,OH YEAH!
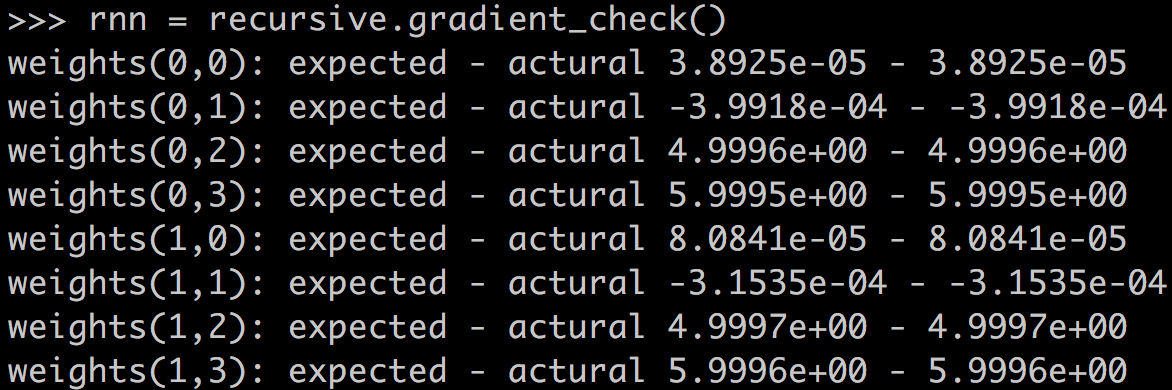
遞迴神經網路的應用
自然語言和自然場景解析
在自然語言處理任務中,如果我們能夠實現一個解析器,將自然語言解析為語法樹,那麼毫無疑問,這將大大提升我們對自然語言的處理能力。解析器如下所示:
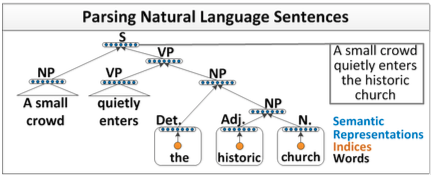
可以看出,遞迴神經網路能夠完成句子的語法分析,併產生一個語法解析樹。
除了自然語言之外,自然場景也具有可組合的性質。因此,我們可以用類似的模型完成自然場景的解析,如下圖所示:
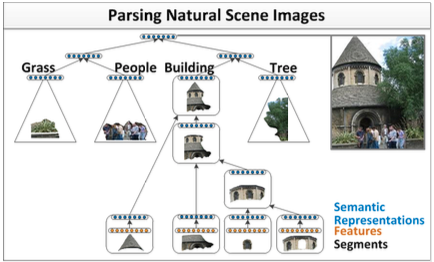
兩種不同的場景,可以用相同的遞迴神經網路模型來實現。我們以第一個場景,自然語言解析為例。
我們希望將一句話逐字輸入到神經網路中,然後,神經網路返回一個解析好的樹。為了做到這一點,我們需要給神經網路再加上一層,負責打分。分數越高,說明兩個子節點結合更加緊密,分數越低,說明兩個子節點結合更鬆散。如下圖所示:
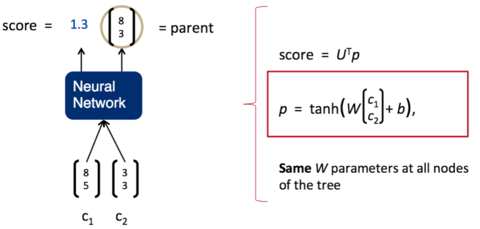
一旦這個打分函式訓練好了(也就是矩陣U的各項值變為合適的值),我們就可以利用貪心演算法來實現句子的解析。第一步,我們先將詞按照順序兩兩輸入神經網路,得到第一組打分:
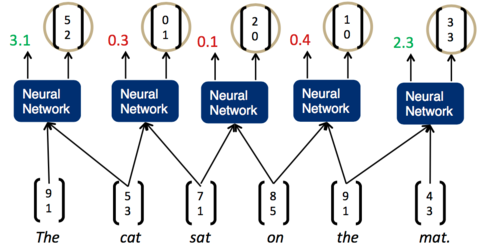
我們發現,現在分數最高的是第一組,The cat,說明它們的結合是最緊密的。這樣,我們可以先將它們組合為一個節點。然後,再次兩兩計算相鄰子節點的打分:
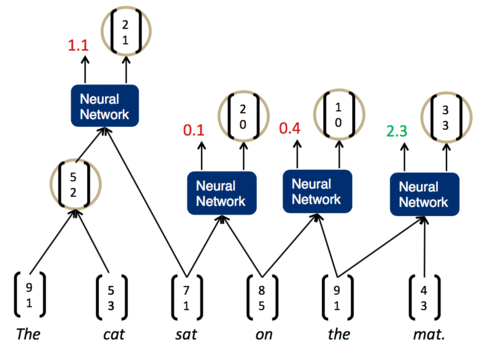
現在,分數最高的是最後一組,the mat。於是,我們將它們組合為一個節點,再兩兩計算相鄰節點的打分:

這時,我們發現最高的分數是on the mat,把它們組合為一個節點,繼續兩兩計算相鄰節點的打分......最終,我們就能夠得到整個解析樹:
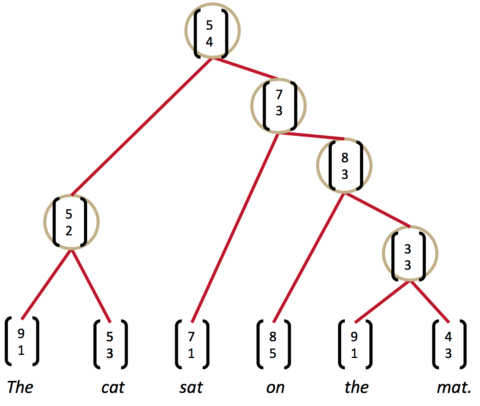


小結

