from：http://www.cnblogs.com/subconscious/p/5058741.html

神經網路是一門重要的機器學習技術。它是目前最為火熱的研究方向--深度學習的基礎。學習神經網路不僅可以讓你掌握一門強大的機器學習方法，同時也可以更好地幫助你理解深度學習技術。

　　本文以一種簡單的，循序的方式講解神經網路。適合對神經網路瞭解不多的同學。本文對閱讀沒有一定的前提要求，但是懂一些機器學習基礎會更好地幫助理解本文。

　　神經網路是一種模擬人腦的神經網路以期能夠實現類人工智慧的機器學習技術。人腦中的神經網路是一個非常複雜的組織。成人的大腦中估計有1000億個神經元之多。

圖1 人腦神經網路

　　那麼機器學習中的神經網路是如何實現這種模擬的，並且達到一個驚人的良好效果的？通過本文，你可以瞭解到這些問題的答案，同時還能知道神經網路的歷史，以及如何較好地學習它。

　　由於本文較長，為方便讀者，以下是本文的目錄：

　　一.前言

　　二.神經元

　　六.回顧

　　七.展望

　　八.總結

　　九.後記

　　十.備註

一. 前言

　　讓我們來看一個經典的神經網路。這是一個包含三個層次的神經網路。紅色的是輸入層，綠色的是輸出層，紫色的是中間層（也叫隱藏層）。輸入層有3個輸入單元，隱藏層有4個單元，輸出層有2個單元。後文中，我們統一使用這種顏色來表達神經網路的結構。

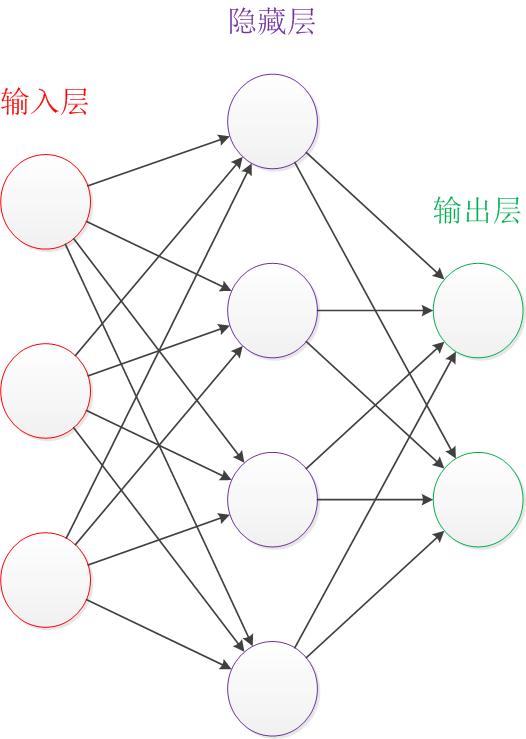
圖2 神經網路結構圖

　　在開始介紹前，有一些知識可以先記在心裡：

1. 設計一個神經網路時，輸入層與輸出層的節點數往往是固定的，中間層則可以自由指定；
2. 神經網路結構圖中的拓撲與箭頭代表著預測過程時資料的流向，跟訓練時的資料流有一定的區別；
3. 結構圖裡的關鍵不是圓圈（代表“神經元”），而是連線線（代表“神經元”之間的連線）。每個連線線對應一個不同的權重（其值稱為權值），這是需要訓練得到的。 

　　除了從左到右的形式表達的結構圖，還有一種常見的表達形式是從下到上來表示一個神經網路。這時候，輸入層在圖的最下方。輸出層則在圖的最上方，如下圖：

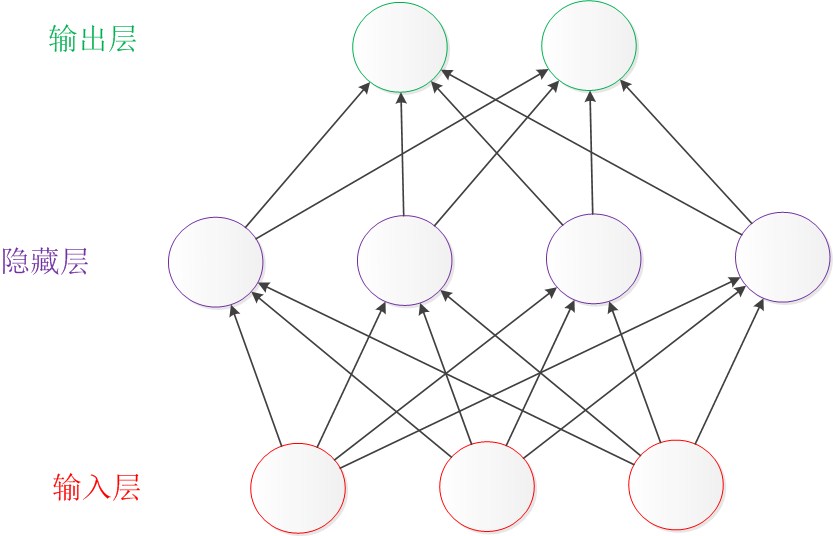
圖3 從下到上的神經網路結構圖 

　　從左到右的表達形式以Andrew Ng和LeCun的文獻使用較多，Caffe裡使用的則是從下到上的表達。在本文中使用Andrew Ng代表的從左到右的表達形式。

下面從簡單的神經元開始說起，一步一步介紹神經網路複雜結構的形成。

二. 神經元

　　1.引子　

　　對於神經元的研究由來已久，1904年生物學家就已經知曉了神經元的組成結構。

　　一個神經元通常具有多個樹突，主要用來接受傳入資訊；而軸突只有一條，軸突尾端有許多軸突末梢可以給其他多個神經元傳遞資訊。軸突末梢跟其他神經元的樹突產生連線，從而傳遞訊號。這個連線的位置在生物學上叫做“突觸”。

　　人腦中的神經元形狀可以用下圖做簡單的說明：

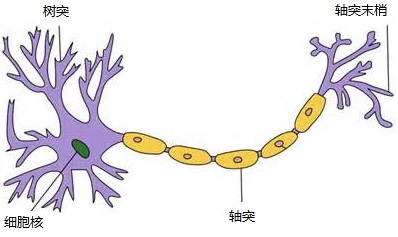
圖4 神經元

 　　1943年，心理學家McCulloch和數學家Pitts參考了生物神經元的結構，發表了抽象的神經元模型MP。在下文中，我們會具體介紹神經元模型。

圖5 Warren McCulloch（左）和 Walter Pitts（右）  

　　2.結構 

　　神經元模型是一個包含輸入，輸出與計算功能的模型。輸入可以類比為神經元的樹突，而輸出可以類比為神經元的軸突，計算則可以類比為細胞核。

　　下圖是一個典型的神經元模型：包含有3個輸入，1個輸出，以及2個計算功能。

　　注意中間的箭頭線。這些線稱為“連線”。每個上有一個“權值”。

圖6 神經元模型 

　　連線是神經元中最重要的東西。每一個連線上都有一個權重。

　　一個神經網路的訓練演算法就是讓權重的值調整到最佳，以使得整個網路的預測效果最好。

　　我們使用a來表示輸入，用w來表示權值。一個表示連線的有向箭頭可以這樣理解：在初端，傳遞的訊號大小仍然是a，端中間有加權引數w，經過這個加權後的訊號會變成a*w，因此在連線的末端，訊號的大小就變成了a*w。

　　在其他繪圖模型裡，有向箭頭可能表示的是值的不變傳遞。而在神經元模型裡，每個有向箭頭表示的是值的加權傳遞。

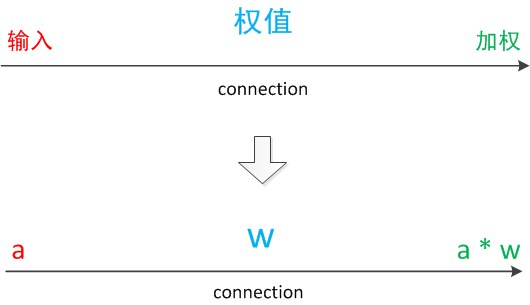
圖7 連線（connection）  

　　如果我們將神經元圖中的所有變數用符號表示，並且寫出輸出的計算公式的話，就是下圖。

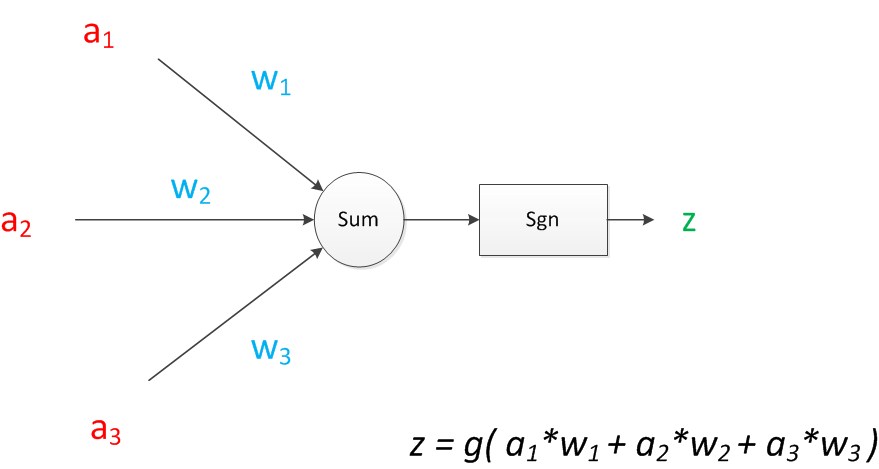
圖8 神經元計算  

　　可見z是在輸入和權值的線性加權和疊加了一個函式g的值。在MP模型裡，函式g是sgn函式，也就是取符號函式。這個函式當輸入大於0時，輸出1，否則輸出0。

　　下面對神經元模型的圖進行一些擴充套件。首先將sum函式與sgn函式合併到一個圓圈裡，代表神經元的內部計算。其次，把輸入a與輸出z寫到連線線的左上方，便於後面畫複雜的網路。最後說明，一個神經元可以引出多個代表輸出的有向箭頭，但值都是一樣的。

　　神經元可以看作一個計算與儲存單元。計算是神經元對其的輸入進行計算功能。儲存是神經元會暫存計算結果，並傳遞到下一層。

圖9 神經元擴充套件 

　　當我們用“神經元”組成網路以後，描述網路中的某個“神經元”時，我們更多地會用“單元”（unit）來指代。同時由於神經網路的表現形式是一個有向圖，有時也會用“節點”（node）來表達同樣的意思。 

　　3.效果 

　　神經元模型的使用可以這樣理解：

　　我們有一個數據，稱之為樣本。樣本有四個屬性，其中三個屬性已知，一個屬性未知。我們需要做的就是通過三個已知屬性預測未知屬性。

　　具體辦法就是使用神經元的公式進行計算。三個已知屬性的值是a₁，a₂，a₃，未知屬性的值是z。z可以通過公式計算出來。

　　這裡，已知的屬性稱之為特徵，未知的屬性稱之為目標。假設特徵與目標之間確實是線性關係，並且我們已經得到表示這個關係的權值w₁，w₂，w₃。那麼，我們就可以通過神經元模型預測新樣本的目標。

　　4.影響

　　1943年釋出的MP模型，雖然簡單，但已經建立了神經網路大廈的地基。但是，MP模型中，權重的值都是預先設定的，因此不能學習。

　　1949年心理學家Hebb提出了Hebb學習率，認為人腦神經細胞的突觸（也就是連線）上的強度上可以變化的。於是計算科學家們開始考慮用調整權值的方法來讓機器學習。這為後面的學習演算法奠定了基礎。

圖10 Donald Olding Hebb 

　　儘管神經元模型與Hebb學習律都已誕生，但限於當時的計算機能力，直到接近10年後，第一個真正意義的神經網路才誕生。

三. 單層神經網路（感知器）

　　1.引子　　

　　1958年，計算科學家Rosenblatt提出了由兩層神經元組成的神經網路。他給它起了一個名字--“感知器”（Perceptron）（有的文獻翻譯成“感知機”，下文統一用“感知器”來指代）。

　　感知器是當時首個可以學習的人工神經網路。Rosenblatt現場演示了其學習識別簡單影象的過程，在當時的社會引起了轟動。

　　人們認為已經發現了智慧的奧祕，許多學者和科研機構紛紛投入到神經網路的研究中。美國軍方大力資助了神經網路的研究，並認為神經網路比“原子彈工程”更重要。這段時間直到1969年才結束，這個時期可以看作神經網路的第一次高潮。

圖11 Rosenblat與感知器 

　　2.結構

　　下面來說明感知器模型。

　　在原來MP模型的“輸入”位置新增神經元節點，標誌其為“輸入單元”。其餘不變，於是我們就有了下圖：從本圖開始，我們將權值w₁, w₂, w₃寫到“連線線”的中間。

圖12 單層神經網路 

　　在“感知器”中，有兩個層次。分別是輸入層和輸出層。輸入層裡的“輸入單元”只負責傳輸資料，不做計算。輸出層裡的“輸出單元”則需要對前面一層的輸入進行計算。

　　我們把需要計算的層次稱之為“計算層”，並把擁有一個計算層的網路稱之為“單層神經網路”。有一些文獻會按照網路擁有的層數來命名，例如把“感知器”稱為兩層神經網路。但在本文裡，我們根據計算層的數量來命名。

　　假如我們要預測的目標不再是一個值，而是一個向量，例如[2,3]。那麼可以在輸出層再增加一個“輸出單元”。

　　下圖顯示了帶有兩個輸出單元的單層神經網路，其中輸出單元z₁的計算公式如下圖。

圖13 單層神經網路(Z₁)

　　可以看到，z₁的計算跟原先的z並沒有區別。

　　我們已知一個神經元的輸出可以向多個神經元傳遞，因此z₂的計算公式如下圖。

圖14 單層神經網路(Z₂)

　　可以看到，z₂的計算中除了三個新的權值：w₄，w₅，w₆以外，其他與z₁是一樣的。

　　整個網路的輸出如下圖。

圖15 單層神經網路(Z₁和Z₂)

　　目前的表達公式有一點不讓人滿意的就是：w₄，w₅，w₆是後來加的，很難表現出跟原先的w₁，w₂，w₃的關係。

　　因此我們改用二維的下標，用w_x,y來表達一個權值。下標中的x代表後一層神經元的序號，而y代表前一層神經元的序號（序號的順序從上到下）。

　　例如，w_1,2代表後一層的第1個神經元與前一層的第2個神經元的連線的權值（這種標記方式參照了Andrew Ng的課件）。根據以上方法標記，我們有了下圖。

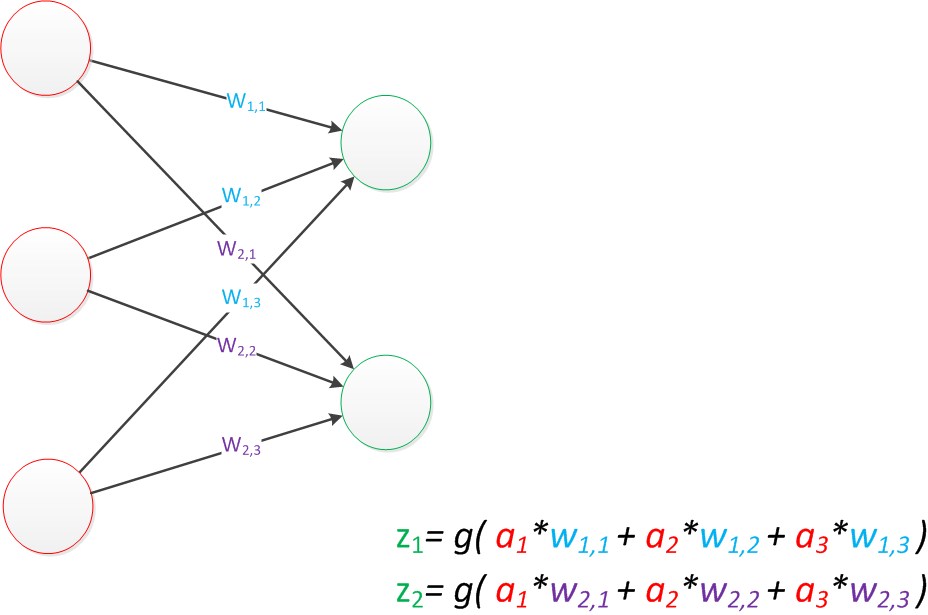
圖16 單層神經網路(擴充套件)

　　如果我們仔細看輸出的計算公式，會發現這兩個公式就是線性代數方程組。因此可以用矩陣乘法來表達這兩個公式。

　　例如，輸入的變數是[a₁，a₂，a₃]^T（代表由a₁，a₂，a₃組成的列向量），用向量a來表示。方程的左邊是[z₁，z₂]^T，用向量z來表示。

　　係數則是矩陣W（2行3列的矩陣，排列形式與公式中的一樣）。

　　於是，輸出公式可以改寫成：

g(W * a) = z;

　　這個公式就是神經網路中從前一層計算後一層的矩陣運算。

　　3.效果

　　與神經元模型不同，感知器中的權值是通過訓練得到的。因此，根據以前的知識我們知道，感知器類似一個邏輯迴歸模型，可以做線性分類任務。

　　我們可以用決策分界來形象的表達分類的效果。決策分界就是在二維的資料平面中劃出一條直線，當資料的維度是3維的時候，就是劃出一個平面，當資料的維度是n維時，就是劃出一個n-1維的超平面。

　　下圖顯示了在二維平面中劃出決策分界的效果，也就是感知器的分類效果。

圖17 單層神經網路（決策分界）

　　4.影響

　　感知器只能做簡單的線性分類任務。但是當時的人們熱情太過於高漲，並沒有人清醒的認識到這點。於是，當人工智慧領域的巨擘Minsky指出這點時，事態就發生了變化。

　　Minsky在1969年出版了一本叫《Perceptron》的書，裡面用詳細的數學證明了感知器的弱點，尤其是感知器對XOR（異或）這樣的簡單分類任務都無法解決。

　　Minsky認為，如果將計算層增加到兩層，計算量則過大，而且沒有有效的學習演算法。所以，他認為研究更深層的網路是沒有價值的。（本文成文後一個月，即2016年1月，Minsky在美國去世。謹在本文中紀念這位著名的計算機研究專家與大拿。）

圖18 Marvin Minsky

　　由於Minsky的巨大影響力以及書中呈現的悲觀態度，讓很多學者和實驗室紛紛放棄了神經網路的研究。神經網路的研究陷入了冰河期。這個時期又被稱為“AI winter”。

　　接近10年以後，對於兩層神經網路的研究才帶來神經網路的復甦。

四. 兩層神經網路（多層感知器）

　　1.引子

　　兩層神經網路是本文的重點，因為正是在這時候，神經網路開始了大範圍的推廣與使用。

　　Minsky說過單層神經網路無法解決異或問題。但是當增加一個計算層以後，兩層神經網路不僅可以解決異或問題，而且具有非常好的非線性分類效果。不過兩層神經網路的計算是一個問題，沒有一個較好的解法。

　　1986年，Rumelhar和Hinton等人提出了反向傳播（Backpropagation，BP）演算法，解決了兩層神經網路所需要的複雜計算量問題，從而帶動了業界使用兩層神經網路研究的熱潮。目前，大量的教授神經網路的教材，都是重點介紹兩層（帶一個隱藏層）神經網路的內容。

　　這時候的Hinton還很年輕，30年以後，正是他重新定義了神經網路，帶來了神經網路復甦的又一春。

圖19 David Rumelhart（左）以及 Geoffery Hinton（右）

　　2.結構

　　兩層神經網路除了包含一個輸入層，一個輸出層以外，還增加了一箇中間層。此時，中間層和輸出層都是計算層。我們擴充套件上節的單層神經網路，在右邊新加一個層次（只含有一個節點）。

　　現在，我們的權值矩陣增加到了兩個，我們用上標來區分不同層次之間的變數。

　　例如a_x^(y)代表第y層的第x個節點。z₁，z₂變成了a₁⁽²⁾，a₂⁽²⁾。下圖給出了a₁⁽²⁾，a₂⁽²⁾的計算公式。

圖20 兩層神經網路（中間層計算）

　　計算最終輸出z的方式是利用了中間層的a₁⁽²⁾，a₂⁽²⁾和第二個權值矩陣計算得到的，如下圖。

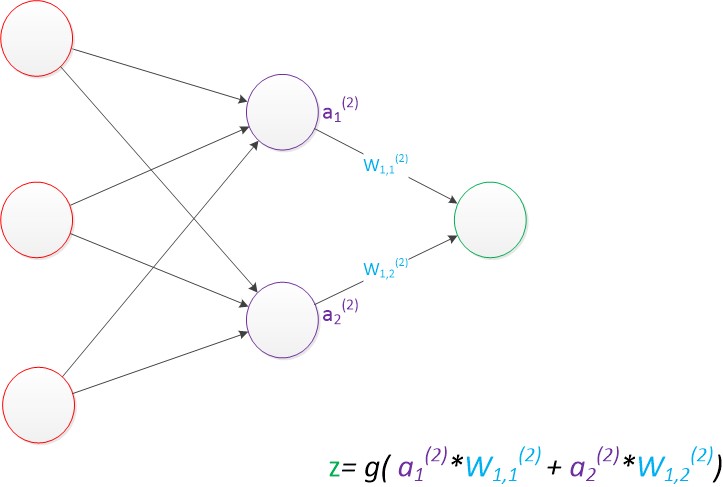
圖21 兩層神經網路（輸出層計算）

　　假設我們的預測目標是一個向量，那麼與前面類似，只需要在“輸出層”再增加節點即可。

　　我們使用向量和矩陣來表示層次中的變數。a⁽¹⁾，a⁽²⁾，z是網路中傳輸的向量資料。W⁽¹⁾和W⁽²⁾是網路的矩陣引數。如下圖。

圖22 兩層神經網路（向量形式）

　　使用矩陣運算來表達整個計算公式的話如下：

  g(W⁽¹⁾ * a⁽¹⁾) = a⁽²⁾; 

g(W⁽²⁾ * a⁽²⁾) = z;

　　由此可見，使用矩陣運算來表達是很簡潔的，而且也不會受到節點數增多的影響（無論有多少節點參與運算，乘法兩端都只有一個變數）。因此神經網路的教程中大量使用矩陣運算來描述。

　　需要說明的是，至今為止，我們對神經網路的結構圖的討論中都沒有提到偏置節點（bias unit）。事實上，這些節點是預設存在的。它本質上是一個只含有儲存功能，且儲存值永遠為1的單元。在神經網路的每個層次中，除了輸出層以外，都會含有這樣一個偏置單元。正如線性迴歸模型與邏輯迴歸模型中的一樣。

　　偏置單元與後一層的所有節點都有連線，我們設這些引數值為向量b，稱之為偏置。如下圖。

圖23 兩層神經網路（考慮偏置節點）

　　可以看出，偏置節點很好認，因為其沒有輸入（前一層中沒有箭頭指向它）。有些神經網路的結構圖中會把偏置節點明顯畫出來，有些不會。一般情況下，我們都不會明確畫出偏置節點。 

　　在考慮了偏置以後的一個神經網路的矩陣運算如下：

  g(W⁽¹⁾ * a⁽¹⁾ + b⁽¹⁾) = a⁽²⁾; 

g(W⁽²⁾ * a⁽²⁾ + b⁽²⁾) = z;

　　需要說明的是，在兩層神經網路中，我們不再使用sgn函式作為函式g，而是使用平滑函式sigmoid作為函式g。我們把函式g也稱作啟用函式（active function）。

　　事實上，神經網路的本質就是通過引數與啟用函式來擬合特徵與目標之間的真實函式關係。初學者可能認為畫神經網路的結構圖是為了在程式中實現這些圓圈與線，但在一個神經網路的程式中，既沒有“線”這個物件，也沒有“單元”這個物件。實現一個神經網路最需要的是線性代數庫。

　　3.效果

　　與單層神經網路不同。理論證明，兩層神經網路可以無限逼近任意連續函式。

　　這是什麼意思呢？也就是說，面對複雜的非線性分類任務，兩