淺析神經網路為什麼能夠無限逼近任意連續函式
神經網路為什麼能夠無限逼近任意連續函式?
下面通過一個分類例子一步一步的引出為什麼神經網路能夠無限逼近任意函式這個觀點,並且給出直觀感覺!
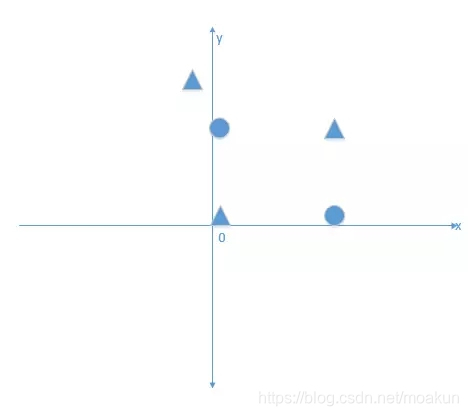
我們首先有這個需求,需要將下面的資料點進行分類,將三角形與正方形正確的分開,如圖所示:
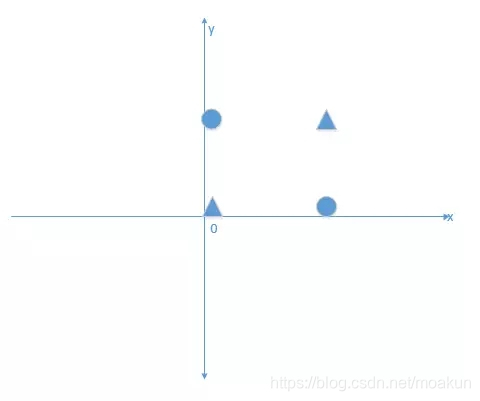
其實上圖就是一個解決一個異或問題。
下面我分別從線性模型,感知機以及神經網路逐步圍繞這個例子來引出自己的觀點。(以下的講解都在二元函式下進行,便於視覺化,高維空間類比)
1.線性模型

如上圖所示,我們什麼啟用函式都不加,那麼輸出結點的公式表達為:y=w1x1+w2x2(注:這裡的1,2均是下標,下文一樣)
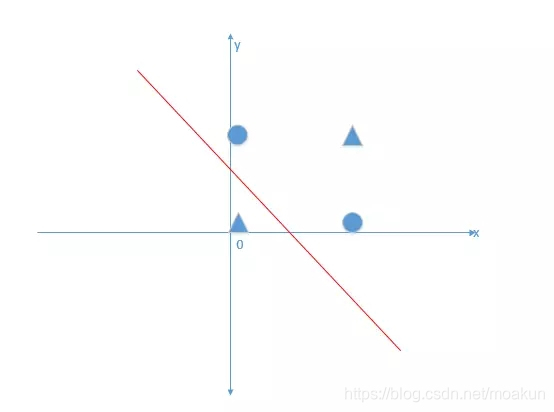
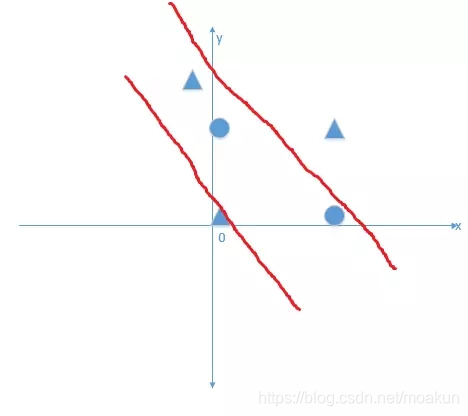
我們希望得到通過訓練資料學習出w1,w2,然後得到線性模型,能夠解決異或問題。但是我們很容易看出,無論怎麼學習,異或問題是一個非線性問題,並不能由一個線性方程能夠正確的將三角形與正方形分隔開!就好像下圖表達一樣,無論你直線怎麼動,都不能正確分離開:
2.感知機
感知機的定義非常簡單,在上面線性模型中的啟用函式變為下面的階梯函式的時候,就是感知機模型。

那麼感知機是否可以解決上面異或問題呢?很顯然並沒有改變它只是線性模型的本質,並不能解決非線性分類問題.因為感知機分類平面投影到二維空間的時候,與下圖是一模一樣的:
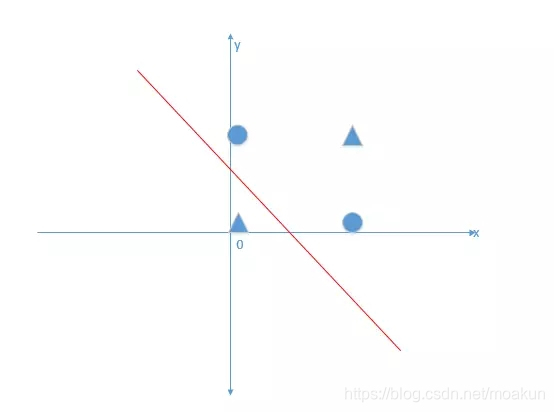
紅線就代表投影方程,比如現在一個輸入點座標為(0,0)帶入方程得到結果為0,那麼就在紅線上,輸入資料帶入模型中,大於0的話,投影下來是在紅線的右側. 小於0的話,投影下來是在紅線的左側.無論怎麼學習(移動)模型,都無法改變感知機是一個線性模型解決不了非線性問題的本質.
3.神經網路
下面我們看多個感知機組合成的神經網路是否能夠解決這個問題呢?答案是肯定能啊,標題是神經網路能夠無限逼近任意連續函式,那麼肯定能夠解決非線性問題,那麼如何解釋呢。下面一步一步給出理解,首先給出一個倆層神經網路結構如下:

很容易看出神經網路就是多個感知機組合而來的,第二層的第一個感知機學到的模型視覺化可以是下面這個:

第二層的第二個感知機學到的模型視覺化可以是下面這個:

那麼在最後一個輸出結點,進行將第二層倆個神經元進行線性組合的時候,得到的視覺化圖是下面這個:
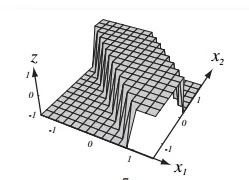
相信到這裡大家已經有感覺了,這不是明擺著已經解決了我提出的問題了嗎,還不信,看下面!
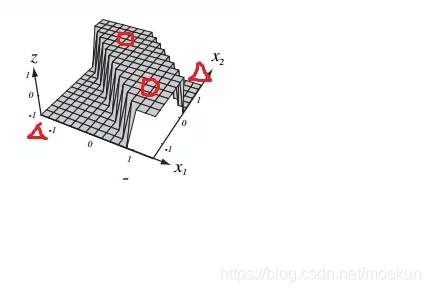
我們已經成功的將圓形與正方形分類出來,圓形對+1這個輸出,三角形對應-1這個輸出,倆個不同的平面上,正確的完成了非線性分類問題。
可能還有些抽象,這麼直白來說,第一個神經元學到的方程可以為x1+x2=1/2對四個資料的輸出分別是:
(0,0)輸出為-1,輸入神經元啟用函式之前的值是小於0(為-1/2)的
(1,0)輸出我+1 輸入神經元啟用函式之前的值是大於0(為1/2)的
(0,1)輸出為+1 輸入神經元啟用函式之前的值是大於0(1/2)的
(1,1)輸出為+1 輸入神經元啟用函式之前的值是大於0(3/2)的
這與我們的預期不一樣,我們希望(0,0)與(1,1)輸出的結果應該一樣,屬於同一類。
根據上圖知道第二個神經元學到的模型x1+x2=7/4對四個資料的輸出分別是:
(0,0)輸出為-1,輸入神經元啟用函式之前的值是小於0(-7/4)的
(1,0)輸出我-1 輸入神經元啟用函式之前的值是小於0(-3/4)的
(0,1)輸出為-1 輸入神經元啟用函式之前的值是小於0(-3/4)的
(1,1)輸出為+1 輸入神經元啟用函式之前的值是大於0(1/2)的
注:以上方程只是為了講解,並不一定是對的!
第三個神經元通過對前面倆個神經元的線性組合,只需要我們通過學習w1,w2來控制(0,0)與(1,1)的輸出同為負數,(1,0)與(0,1)的輸出同為正,那麼就完成了我們的任務,也滿足了我上圖的結論,正確分類了.也就是說,
我們希望得到下面的結論:
代入(-1,-1)的時候,模型輸出為-1
代入(+1,-1)的時候,模型輸出為+1
代入(+1,+1)的時候,模型輸出為-1
也就是說滿足:-w1-w2+b<0
w1-w2+b>0
w1+w2+b<0
很容易通過學習w1,w2,b得到這樣的模型,比如5x1-2x2-4=0(x1為第一個神經元的輸出,x2為第二個神經元的輸出,注意通過階梯函式,輸出只能是+1,-1了),滿足了我們的分類要求!!已經成功的解決了異或問題。
可能有同學會問,你這僅僅只解決了異或問題呀?那加入其它限制條件呢?比如說下圖:
如果是上圖的非線性分類問題,不僅僅是簡單的異或問題,神經網路能夠解決嗎?答案是肯定的,我們可以在隱藏層加一個神經元,在一開始倆個神經元的作用下,再加入一個神經元,它起到的線性效果是下圖(這裡為了簡單方便,我就畫一下投影圖):
在沒有加入第三個神經元的時候,投影圖如下(倆個紅線之內的是輸出為+1的樣本,之外的為輸出為-1的樣本):
但是這個圖只能解決異或問題,並不能將最上面三角形正確分類,我們新加入的神經元起到的效果只要滿足下面這個條件即可: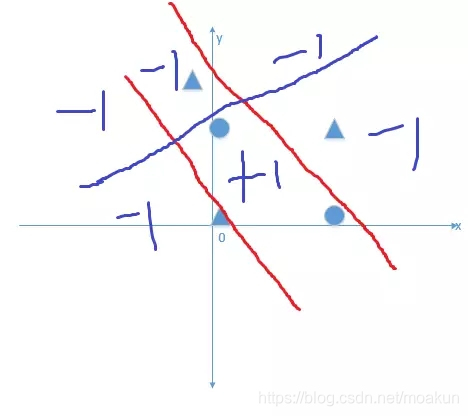
我們就很容易得到結論,我們又可以正確將要求的樣本正確分類了(每個區域應該屬於哪個輸出-1還是+1,為了直觀我在圖上畫出來了~)!那麼無論你是什麼樣的資料樣本,我都可以理論上加入無數個隱藏層神經元來逼近任意連續函式進行我們的任務(有一個結論是無數個直線能夠逼近任意連續曲線,道理是一樣的)。
下面給出四個隱藏神經元的輸出層視覺化效果,這次的啟用函式也不會階梯函數了,可能是sigmoid或者tanh等其它非線性啟用函式,但這些都不影響表達的本質。
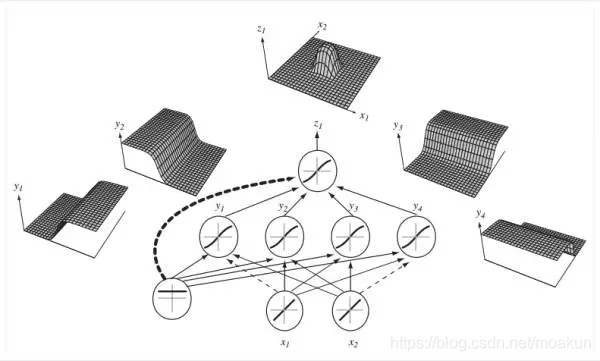
到這裡,我已經講完了我要說的內容了,只是根據自己的理解通過非常簡單的例子想給大家一個直觀上的認識和理解,希望能對大家理解有幫助,歡迎大家指錯交流~
部分圖片來自於:Hugo Larochelle課程的slides
