這裡我來集中分析一下七大排序演算法的效能問題。如果不當之處，敬請指正。

氣泡排序（Bubble）

氣泡排序演算法裡面含有2層迴圈，顯然最壞時間複雜度為O（n2），這裡可能很多人不懂平均情況下的複雜度是什麼意思，下面引用一段話：

• 而平均執行時間也就是從概率的角度看，這個數字在每一個位置的可能性是相同的，所以平均的查詢時間為n/2次後發現這個目標元素。平均情況更能反映大多數情況下演算法的表現。平均情況分析就是對所有輸入尺寸為n的輸入，讓演算法運轉一遍，然後取它們的平均值。當然，實際中不可能將所有可能的輸入都執行一遍，因此平均情況通常指的是一種數學期望值，而計算數學期望值則需要對輸入的分佈情況進行假設。
• 平均執行時間是所有情況中最有意義的，因為它是期望的執行時間。也就是說，我們執行一段程式程式碼時，是希望看到平均執行時間的。可現實中，平均執行時間很難通過分析得到，一般都是通過執行一定數量的實驗資料後估算出來的。

那麼為什麼氣泡排序最好情況下的複雜度為O（n）呢？其實用我們最初的氣泡排序程式碼，其最好情況下複雜度依然為O（n2）。如果氣泡排序演算法在原來的基礎上改進如下：

    public static void b_getsort(int[] a)
    {
        int len = a.length;
        int i,j;
        boolean
 
 flag = true;
        for(i=0;i<len-1&&flag;i++)
        {
            flag = false;
            for(j = 0;j<len-1-i;j++)
            {
                if (a[j]>a[j+1])
                {
                    int temp = a[j];
                    a[j] = a[j+1];
                    a[j+1] = a[j];
                    flag = true
 
;
                }
            }
        }
    }

設定了一個flag變數用來標示我們操作的那部分資料是否發生了資料交換。
比如說，在我們第一次‘冒’的時候，均未發生過交換（即原陣列本身是有序的），那麼flag就是為false，這也就意味著我們根本不必再進行第二次、第三次的‘冒泡’。其實這也就是最好的情況，即只進行了一次對陣列所有元素的訪問。

簡單選擇排序（Select Sort）

簡單選擇排序也是2層迴圈，因而也是O（n2）。

插入排序（Insert Sort）

插入排序跟氣泡排序的效能是一樣的。

希爾排序（Shell Sort）

寫到這兒，我感覺有必要普及一下幾種常用的演算法複雜度。
常見的演算法時間複雜度由小到大依次為：Ο(1)＜Ο(logn)＜Ο(n)＜Ο(nlogn)＜Ο(n2)＜Ο(n3)＜…＜Ο(2n)＜Ο(n!)

在希爾排序中，增量的選取十分關鍵。“可究竟選取什麼樣的增量才是最好，目前還是一個數學難題，迄
今為止還沒有人找到一種最好的增量序列。不過大量的研究表明，當增量序列為
dlta[k]=2t−k+1−1，0≤k≤t≤⌊log2(n+1)⌋”時，可以獲得不錯的效率，其時間複雜度為O（n3/2），要好於直接排序的O（n2）。需要注意的是，增量序列的最後的一個增量值必須等於1才行。另外由於記錄是跳躍式的移動，希爾排序並不是一種穩定的排序演算法。不管怎麼說，希爾排序演算法的發明，使得我們終於突破了慢速排序的時代（超越了時間複雜度為O（n2））”———>引自《大話資料結構》。

不過至於平均情況複雜度為什麼會為O（nlogn），我也沒搞清楚。反正它的複雜度位於Ο(n)和Ο(n2)之間。

快速排序

快速排序的平均時間為Tavg（n）=knln(n),其中n為待排序記錄中記錄的個數，k為某個常數，經驗證明，在所有同數量級的此類（先進的）排序方法中，快速排序的常數因子k最小。因此，就平均時間而言，快速排序是目前被認為是最好的一種內部排序方法。——>《資料結構（C語言版）》，嚴蔚敏 吳偉民著

由於快速排序的演算法複雜度分析涉及太多數學知識，這裡不做過多分析。不過我們應該注意快排的空間複雜度以及穩定性。

歸併排序

從上表可以看出，三種情況下歸併排序的複雜度都為O（nlogn），空間複雜度為O（n）。

堆排序

這裡我們可以拿堆排序和歸併排序比較一下，二者時間複雜度相同，但是穩定性和空間複雜度方面有差別。

最後，我來綜合說一下幾個面試問的比較多的問題。

• 演算法的穩定性？

演算法的穩定性是指在序列中關鍵字相同的元素，經過某種排序演算法之後，這些元素之間的順序保持不變。如果發生改變，那麼就稱該演算法是不穩定的。

• 演算法的不穩定和穩定會分別導致什麼？

①實際排序中，我們操作的可能不是整數，可能是一些很大的物件，而交換元素 產生的開銷對程式效能的影響便會很大
②基數排序（將操作元素劃分為多個關鍵字進行排序，比如很多學生的資料，首先按照班級排序，然後班級相同的再按照年齡排序，如此等等）在不穩定排序演算法中無法完成。

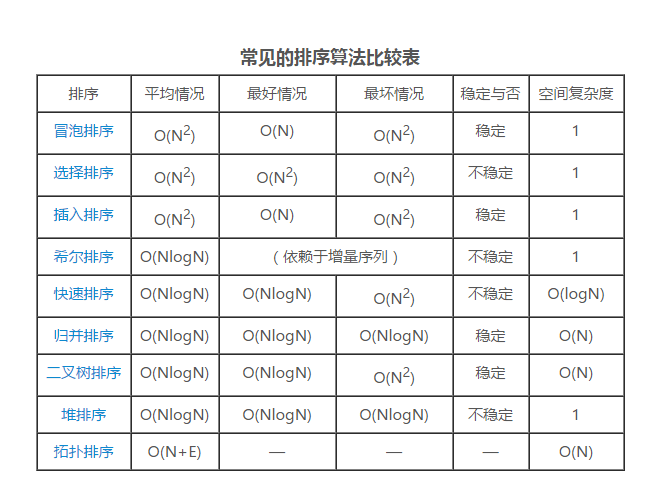
最後來個總結圖（來自倪升武的部落格）