《ORB: an efficient alternative to SIFT or SURF》是Rublee等人在2011年的ICCV上發表的一篇有關於特徵點提取和匹配的論文，這篇論文介紹的方法跳出了SIFT和SURF演算法的專利框架，同時以極快的執行速度贏得了眾多青睞。下面我簡單介紹一下ORB演算法的流程。

ORB演算法的主要貢獻如下：
（1）為FAST演算法提取的特徵點加上了一個特徵點方向；
（2）使用帶方向的BRIEF演算法高效的對特徵點描述符進行計算；
（3）分析了BRIEF演算法得到的特徵點描述符的方差和關聯性；
（4）介紹了一種基於學習的去特徵點關聯性的BRIEF演算法，優化了特徵點求得的最近鄰點。

下面我按照論文的結構對ORB演算法進行介紹。

1、oFAST: FAST Keypoint Orientation

1.1 FAST Detector

ORB演算法使用的是FAST演算法提取的特徵點（FAST演算法介紹見我的博文特徵點匹配——FAST演算法介紹），在作者的實驗中使用的FAST-9的演算法，得到了很好的結果。
由於邊緣位置對FAST演算法得到的特徵點有很大的影響，因此作者使用了Harris 角點檢測方法對於得到的特徵點進行排序，取前N個較好的角點作為特徵點。

FAST演算法是一種非常快的提取特徵點的方法，但是對於這裡來說，有兩點不足：
（1）提取到的特徵點沒有方向；
（2）提取到的特徵點不滿足尺度變化。
針對特徵點不滿足尺度變化，作者像SIFT演算法中那樣，建立尺度影象金字塔，通過在不同尺度下的影象中提取特徵點以達到滿足尺度變化的效果。
針對提取到的特徵點沒有方向的問題，作者採用了Rosin提出的一種稱為“intensity centroid”的方法確定了特徵點的方向。
那麼，就來看一下確定特徵點方向的方法。

1.2 Orientation by Intensity Centroid

這種方法的主要思想就是，首先把特徵點的鄰域範圍看成一個patch，然後求取這個patch的質心，最後把該質心與特徵點進行連線，求出該直線與橫座標軸的夾角，即為該特徵點的方向。
那麼，怎麼求取這個鄰域的質心呢？
論文中提到Rosin定義瞭如下公式：

mpq=∑x,yxpyqI(x,y)然後質心定義為：C=(m10m00,m01m00)然後求取向量OC的方向，同時如果把x,y的範圍保持在[−r,r]之間（r為該特徵點鄰域的半徑），以特徵點為座標原點，則得到的方向角為θ=atan2(m01,m10)
作者在論文中提到，這種演算法比BIN和MAX這兩種求取特徵點方向的方法都要好。

2、rBRIEF: Rotation-Aware Brief

2.1 Efficient Rotation of the BRIEF Operator Brief overview of BRIEF

下面我們隊BRIEF演算法進行一個簡單的回顧：
BRIEF演算法提取得到的特徵點描述符是一個二進位制的字串，建設當前的一個特徵點的鄰域空間patch，設為p，那麼對該面片p定義的一個二進位制測試

τ(p;x,y):={1:p(x)<p(y)0:p(x)≥p(y)}其中p(x)表示的是在點x處的影象灰度值，那麼這樣我們就可以得到一個n位的二進位制串fn(p):=∑1≤i≤n2i−1τ(p;xi,yi)對於x和y的座標分佈在本文中使用的是以特徵點為中心的高斯分佈，這種分佈情況在Brief的論文原文中被證明是最好的。同樣，本文中選擇的n=256。
考慮到影象中有噪聲的干擾，在實際的求取特徵點描述符的過程中，需要對影象進行平滑操作。論文中使用的方法是，在對比操作τ進行的時候，不是對比的一個點，而是對比的在31∗31的patch中的若干個5∗5的子視窗。
上面就是BRIEF演算法的一個簡單回顧，BRIEF演算法形成的描述符對於旋轉操作非常敏感，當旋轉的角度增大時，利用BRIEF演算法的描述符進行匹配的結果極大的降低。如下圖所示：
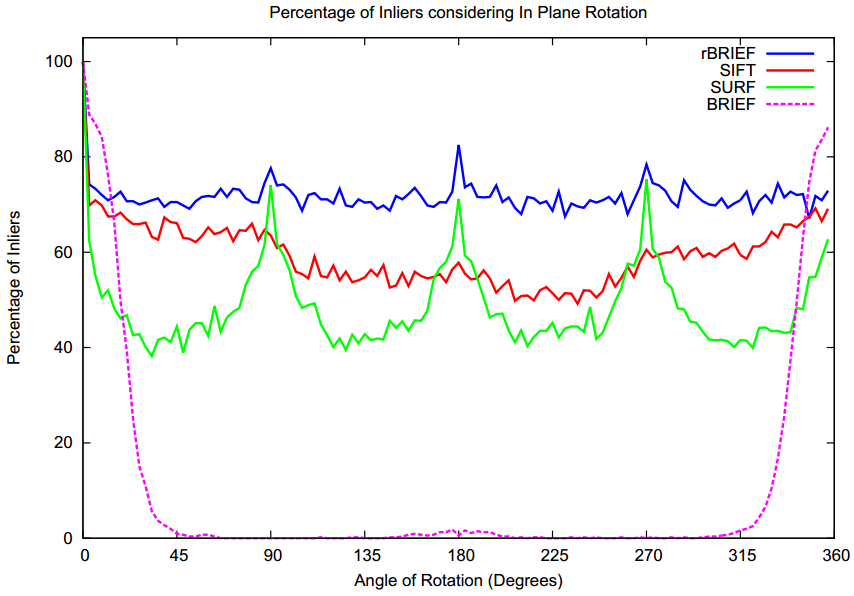
圖中x軸表示的是旋轉的角度，y軸表示匹配結果中正確匹配所佔的百分比。可以看出，隨著旋轉角度的增大，BRIEF演算法的匹配效果迅速的降低，旋轉角度在45度以上時，正確率幾乎為0。那麼這就引出了我們接下來要介紹的Steered BRIEF演算法。

Steered BRIEF演算法介紹

想要讓BRIEF演算法具有旋轉不變性，那麼我們需要使特徵點的鄰域旋轉一個角度，該角度就是我們上面求得的特徵點的方向角θ。但是這樣整體旋轉一個鄰域的開銷是比較大的，一個更加高效的做法就是旋轉我們前面得到的那些鄰域中的匹配點xi、yi。
設生成特徵點描述符的n個測試點對為(xi,yi)，定義一個2×n的矩陣

S=(x1,y1,......,xn,yn)利用角度θ形成的旋轉矩陣為Rθ，那麼旋轉後匹配點的座標為Sθ=RθS這樣，在求取特徵點描述符的時候，就使用Sθ中的畫素點即可。

2.2 Variance and Correlation

作者提到，BRIEF的一個比較好的特性是，對於所有的特徵點上的每一位（bit）上的值的平均值都非常接近0.5（這裡的平均值比較難理解，舉個例子，比如說n個特徵點中的所有的第i位的平均值），同時平均值的分佈的方差較大。這樣很顯然有一個好處，就是方差越大說明資料的差異性越大，也就是說更能很好的區分不同的點。下圖為作者取100k個特徵點中的256位中各位的平均值分佈，其中橫座標為平均值與0.5的差值，縱座標是位的個數：

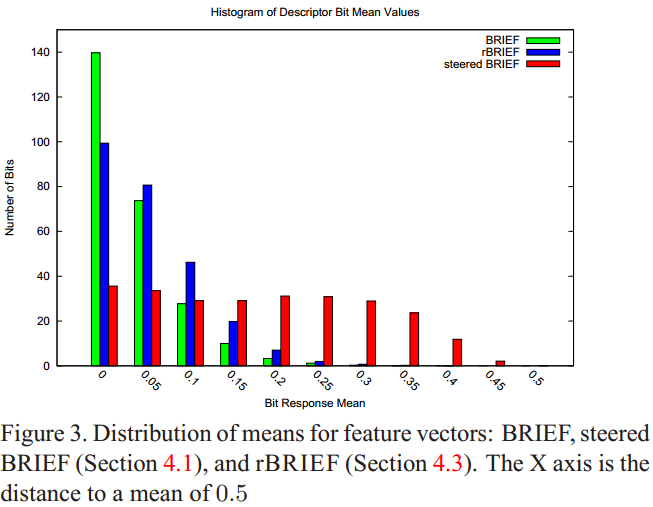
可以看出BRIEF的所有特徵點各個位上的平均值分佈為以0.5為均值，方差很大的一個高斯分佈。
同樣看上面這個圖，我們發現steered BRIEF演算法的結果中，所有特徵點在各個位上的平均的分佈則比較平均，這是因為進行旋轉角度θ以後，均值就漂移到更加均衡的模式。
作者同時對BRIEF、Steered BRIEF和rBRIEF（後面會講到）提取的100k個特徵點的描述符進行PCA提取主成份，根據得到的特徵值進行分析，如下圖所示：

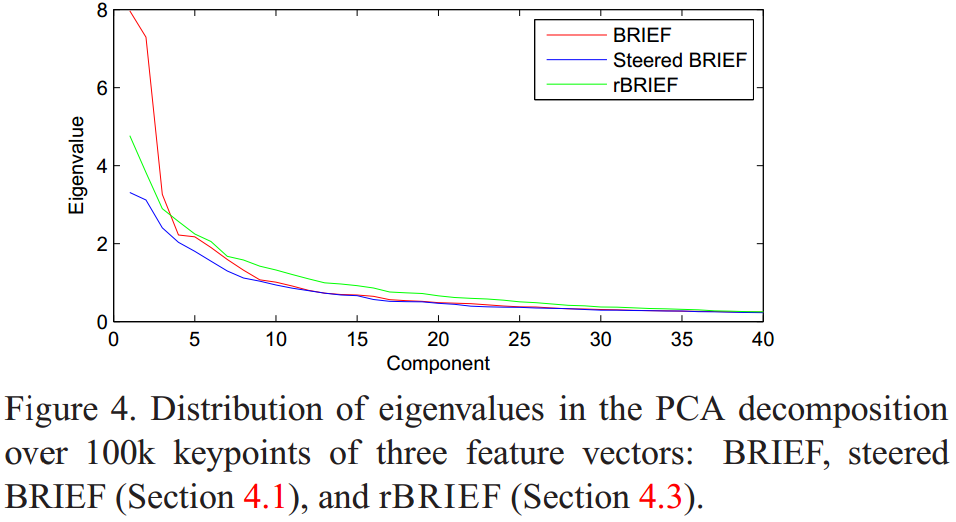
可以看出BRIEF和Steered BRIEF中前幾個特徵值比較大，那麼基本上所有的資訊都集中在這這面的若干維中，而Steered BRIEF演算法得到的特徵值比BRIEF的特徵值小很多，因此Steered BRIEF得到的描述符的方差分佈小，也就意味的區分能力比較差。
我們從另一個角度也可以證實這一點，如下圖所示，實線表示的是匹配成功的點的距離的分佈，虛線表示的是匹配失敗的點的距離的分佈，橫座標是距離，縱座標是頻率：

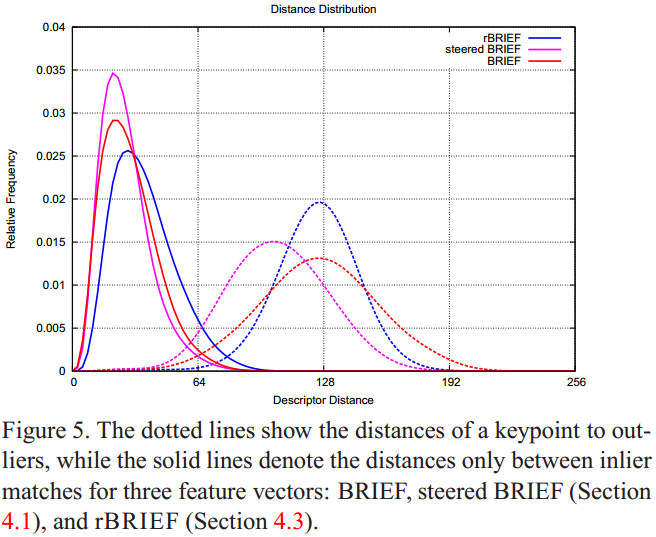
可以看出相比BRIEF和rBRIEF，steered BRIEF得到的匹配結果中，匹配失敗的點的距離分佈的平均值推左（論文中的push left，其實就是平均值偏小）了，這也就造成了成功和失敗的點的距離中有更多的交集。同時也就意味著匹配結果的不理想。

2.3 Learning Good Binary Features

為了彌補Steered BRIEF演算法造成的方差變小的缺陷，同時降低各個特徵點的鄰域內的匹配點對的相關性，作者使用了一種學習的方法來從鄰域的所有可能的匹配點對中選出一個表現較好的子集用來生成特徵點描述符。
作者首先從PASCAL 2006的影象庫中提取了300k個特徵點作為訓練集，然後從每個特徵點的31×31大小的鄰域中窮舉出所有可能的5×5的匹配子視窗。假設wp為總鄰域的邊長，wt作為子視窗的邊長，那麼再這個鄰域中一共有N=(wp−wt)2個子視窗存在，從其中任意挑選2個子視窗，則有(N2