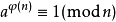轉載自http://blog.csdn.net/Cold_Chair/article/details/52235196

內容：

在數論中，尤拉定理,(也稱費馬-尤拉定理)是一個關於同餘的性質。尤拉定理表明，若n,a為正整數，且n,a互質，則:

摺疊證明：

將1~n中與n互質的數按順序排布:x1,x2……xφ(n) (顯然，共有φ(n)個數)

我們考慮這麼一些數:

m1=a*x1;m2=a*x2;m3=a*x3……mφ(n)=a*xφ(n)

(1)

這些數中的任意兩個都不模n同餘，因為如果有mS≡mR (mod n) (這裡假定mS更大一些)，就有:

mS-mR=a(xS-xR)=qn，即n能整除a(xS-xR)。但是a與n互質，a與n的最大公因子是1，而xS-xR<n

n,因而左式不可能被n整除。也就是說這些數中的任意兩個都不模n同餘，φ(n)個數有φ(n)種餘數。

(2)

這些數除n的餘數都與n互質： 
我們知道a，xi與n互質，則a × xi 與n互質，根據歐幾里得演算法，則n與（a × xi） %n也互質 。

那麼這些數除n的餘數，都在x1,x2,x3……xφ(n)中，因為這是1~n中與n互質的所有數，而餘數又小於n.

由(1)和(2)可知，數m1,m2,m3……mφ(n)(如果將其次序重新排列)必須相應地同餘於x1,x2,x3……xφ(n).

故得出:m1*m2*m3……mφ(n)≡x1*x2*x3……xφ(n) (mod n)

或者說a^[φ(n)]*(x1*x2*x3……xφ(n))≡x1*x2*x3……xφ(n)

或者為了方便:K{a^[φ(n)]-1}≡0 ( mod n ) 這裡K=x1*x2*x3……xφ(n)。

可知K{a^[φ(n)]-1}被n整除。但K中的因子x1,x2……都與n互質，所以K與n互質。那麼a^[φ(n)]-1必須能被n整除，即a^[φ(n)]-1≡0 (mod n)，即a^[φ(n)]≡1 (mod n)，得證。

費馬小定理:

a是不能被質數p整除的正整數，則有a^(p-1) ≡ 1 (mod p)

證明這個定理非常簡單，由於p是質數，所以有φ(p) = p-1，代入尤拉定理即可證明。推論:對於任意正整數a，有a^p ≡ a (mod p)，因為a能被p整除時結論顯然成立。