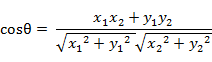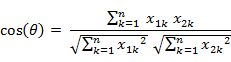概率分佈之間的距離度量以及python實現
原文連結：https://www.cnblogs.com/wt869054461/p/7156397.html
1. 歐氏距離(Euclidean Distance)
歐氏距離是最易於理解的一種距離計算方法，源自歐氏空間中兩點間的距離公式。
(1)二維平面上兩點a(x1,y1)與b(x2,y2)間的歐氏距離：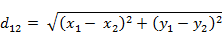
(2)三維空間兩點a(x1,y1,z1)與b(x2,y2,z2)間的歐氏距離：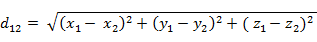
(3)兩個n維向量a(x11,x12,…,x1n)與 b(x21,x22,…,x2n)間的歐氏距離：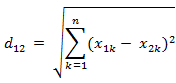
(4)也可以用表示成向量運算的形式：
python中的實現：
方法一：
import numpy as np x=np.random.random(10) y=np.random.random(10) #方法一：根據公式求解 d1=np.sqrt(np.sum(np.square(x-y))) #方法二：根據scipy庫求解 from scipy.spatial.distance import pdist X=np.vstack([x,y]) d2=pdist(X)
2. 曼哈頓距離(Manhattan Distance)
從名字就可以猜出這種距離的計算方法了。想象你在曼哈頓要從一個十字路口開車到另外一個十字路口，駕駛距離是兩點間的直線距離嗎？顯然不是，除非你能穿越大樓。實際駕駛距離就是這個“曼哈頓距離”。而這也是曼哈頓距離名稱的來源， 曼哈頓距離也稱為城市街區距離(City Block distance)。
(1)二維平面兩點a(x1,y1)與b(x2,y2)間的曼哈頓距離
(2)兩個n維向量a(x11,x12,…,x1n)與 b(x21,x22,…,x2n)間的曼哈頓距離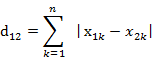
python中的實現 ：
import numpy as np x=np.random.random(10) y=np.random.random(10) #方法一：根據公式求解 d1=np.sum(np.abs(x-y)) #方法二：根據scipy庫求解 from scipy.spatial.distance import pdist X=np.vstack([x,y]) d2=pdist(X,'cityblock')
3. 切比雪夫距離 ( Chebyshev Distance )
國際象棋玩過麼？國王走一步能夠移動到相鄰的8個方格中的任意一個。那麼國王從格子(x1,y1)走到格子(x2,y2)最少需要多少步？自己走走試試。你會發現最少步數總是max( | x2-x1 | , | y2-y1 | ) 步 。有一種類似的一種距離度量方法叫切比雪夫距離。
(1)二維平面兩點a(x1,y1)與b(x2,y2)間的切比雪夫距離
(2)兩個n維向量a(x11,x12,…,x1n)與 b(x21,x22,…,x2n)間的切比雪夫距離
這個公式的另一種等價形式是
看不出兩個公式是等價的？提示一下：試試用放縮法和夾逼法則來證明。
在python中的實現：
import numpy as np x=np.random.random(10) y=np.random.random(10) #方法一：根據公式求解 d1=np.max(np.abs(x-y)) #方法二：根據scipy庫求解 from scipy.spatial.distance import pdist X=np.vstack([x,y]) d2=pdist(X,'chebyshev')
4. 閔可夫斯基距離(Minkowski Distance)
閔氏距離不是一種距離，而是一組距離的定義。
(1) 閔氏距離的定義
兩個n維變數a(x11,x12,…,x1n)與 b(x21,x22,…,x2n)間的閔可夫斯基距離定義為：
也可寫成
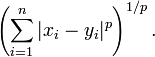
其中p是一個變引數。
當p=1時，就是曼哈頓距離
當p=2時，就是歐氏距離
當p→∞時，就是切比雪夫距離
根據變引數的不同，閔氏距離可以表示一類的距離。
(2)閔氏距離的缺點
閔氏距離，包括曼哈頓距離、歐氏距離和切比雪夫距離都存在明顯的缺點。
舉個例子：二維樣本(身高,體重)，其中身高範圍是150~190，體重範圍是50~60，有三個樣本：a(180,50)，b(190,50)，c(180,60)。那麼a與b之間的閔氏距離（無論是曼哈頓距離、歐氏距離或切比雪夫距離）等於a與c之間的閔氏距離，但是身高的10cm真的等價於體重的10kg麼？因此用閔氏距離來衡量這些樣本間的相似度很有問題。
簡單說來，閔氏距離的缺點主要有兩個：(1)將各個分量的量綱(scale)，也就是“單位”當作相同的看待了。(2)沒有考慮各個分量的分佈（期望，方差等)可能是不同的。
python中的實現：
import numpy as np x=np.random.random(10) y=np.random.random(10) #方法一：根據公式求解,p=2 d1=np.sqrt(np.sum(np.square(x-y))) #方法二：根據scipy庫求解 from scipy.spatial.distance import pdist X=np.vstack([x,y]) d2=pdist(X,'minkowski',p=2)
5. 標準化歐氏距離 (Standardized Euclidean distance )
(1)標準歐氏距離的定義
標準化歐氏距離是針對簡單歐氏距離的缺點而作的一種改進方案。標準歐氏距離的思路：既然資料各維分量的分佈不一樣，好吧！那我先將各個分量都“標準化”到均值、方差相等吧。均值和方差標準化到多少呢？這裡先複習點統計學知識吧，假設樣本集X的均值(mean)為m，標準差(standard deviation)為s，那麼X的“標準化變數”表示為：
標準化後的值 = ( 標準化前的值 － 分量的均值 ) /分量的標準差
經過簡單的推導就可以得到兩個n維向量a(x11,x12,…,x1n)與 b(x21,x22,…,x2n)間的標準化歐氏距離的公式：
如果將方差的倒數看成是一個權重，這個公式可以看成是一種加權歐氏距離(Weighted Euclidean distance)。
python中的實現：
import numpy as np x=np.random.random(10) y=np.random.random(10) X=np.vstack([x,y]) #方法一：根據公式求解 sk=np.var(X,axis=0,ddof=1) d1=np.sqrt(((x - y) ** 2 /sk).sum()) #方法二：根據scipy庫求解 from scipy.spatial.distance import pdist d2=pdist(X,'seuclidean')
6. 馬氏距離(Mahalanobis Distance)
（1）馬氏距離定義
有M個樣本向量X1~Xm，協方差矩陣記為S，均值記為向量μ，則其中樣本向量X到u的馬氏距離表示為：
而其中向量Xi與Xj之間的馬氏距離定義為：
若協方差矩陣是單位矩陣（各個樣本向量之間獨立同分布）,則公式就成了：
也就是歐氏距離了。
若協方差矩陣是對角矩陣，公式變成了標準化歐氏距離。
python 中的實現：
import numpy as np
x=np.random.random(10)
y=np.random.random(10)
#馬氏距離要求樣本數要大於維數，否則無法求協方差矩陣
#此處進行轉置，表示10個樣本，每個樣本2維
X=np.vstack([x,y])
XT=X.T
#方法一：根據公式求解
S=np.cov(X) #兩個維度之間協方差矩陣
SI = np.linalg.inv(S) #協方差矩陣的逆矩陣
#馬氏距離計算兩個樣本之間的距離，此處共有10個樣本，兩兩組合，共有45個距離。
n=XT.shape[0]
d1=[]
for i in range(0,n):
for j in range(i+1,n):
delta=XT[i]-XT[j]
d=np.sqrt(np.dot(np.dot(delta,SI),delta.T))
d1.append(d)
#方法二：根據scipy庫求解
from scipy.spatial.distance import pdist
d2=pdist(XT,'mahalanobis')
馬氏優缺點：
1）馬氏距離的計算是建立在總體樣本的基礎上的，這一點可以從上述協方差矩陣的解釋中可以得出，也就是說，如果拿同樣的兩個樣本，放入兩個不同的總體中，最後計算得出的兩個樣本間的馬氏距離通常是不相同的，除非這兩個總體的協方差矩陣碰巧相同；
2）在計算馬氏距離過程中，要求總體樣本數大於樣本的維數，否則得到的總體樣本協方差矩陣逆矩陣不存在，這種情況下，用歐式距離計算即可。
3）還有一種情況，滿足了條件總體樣本數大於樣本的維數，但是協方差矩陣的逆矩陣仍然不存在，比如三個樣本點（3，4），（5，6）和（7，8），這種情況是因為這三個樣本在其所處的二維空間平面內共線。這種情況下，也採用歐式距離計算。
4）在實際應用中“總體樣本數大於樣本的維數”這個條件是很容易滿足的，而所有樣本點出現3）中所描述的情況是很少出現的，所以在絕大多數情況下，馬氏距離是可以順利計算的，但是馬氏距離的計算是不穩定的，不穩定的來源是協方差矩陣，這也是馬氏距離與歐式距離的最大差異之處。
優點：它不受量綱的影響，兩點之間的馬氏距離與原始資料的測量單位無關；由標準化資料和中心化資料(即原始資料與均值之差）計算出的二點之間的馬氏距離相同。馬氏距離還可以排除變數之間的相關性的干擾。缺點：它的缺點是誇大了變化微小的變數的作用。
7. 夾角餘弦(Cosine)
也可以叫餘弦相似度。 幾何中夾角餘弦可用來衡量兩個向量方向的差異，機器學習中借用這一概念來衡量樣本向量之間的差異。
(1)在二維空間中向量A(x1,y1)與向量B(x2,y2)的夾角餘弦公式：
(2) 兩個n維樣本點a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夾角餘弦
類似的，對於兩個n維樣本點a(x11,x12,…,x1n)和b(x21,x22,…,x2n)，可以使用類似於夾角餘弦的概念來衡量它們間的相似程度。
即：
餘弦取值範圍為[-1,1]。求得兩個向量的夾角，並得出夾角對應的餘弦值，此餘弦值就可以用來表徵這兩個向量的相似性。夾角越小，趨近於0度，餘弦值越接近於1，它們的方向更加吻合，則越相似。當兩個向量的方向完全相反夾角餘弦取最小值-1。當餘弦值為0時，兩向量正交，夾角為90度。因此可以看出，餘弦相似度與向量的幅值無關，只與向量的方向相關。
import numpy as np x=np.random.random(10) y=np.random.random(10) #方法一：根據公式求解 d1=np.dot(x,y)/(np.linalg.norm(x)*np.linalg.norm(y)) #方法二：根據scipy庫求解 from scipy.spatial.distance import pdist X=np.vstack([x,y]) d2=1-pdist(X,'cosine')
兩個向量完全相等時，餘弦值為1，如下的程式碼計算出來的d=1。
d=1-pdist([x,x],'cosine')
8. 皮爾遜相關係數（Pearson correlation）
(1) 皮爾遜相關係數的定義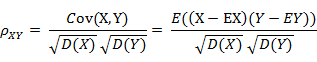
前面提到的餘弦相似度只與向量方向有關，但它會受到向量的平移影響，在夾角餘弦公式中如果將 x 平移到 x+1, 餘弦值就會改變。怎樣才能實現平移不變性？這就要用到皮爾遜相關係數（Pearson correlation），有時候也直接叫相關係數。
如果將夾角餘弦公式寫成：
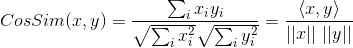
表示向量x和向量y之間的夾角餘弦，則皮爾遜相關係數則可表示為：
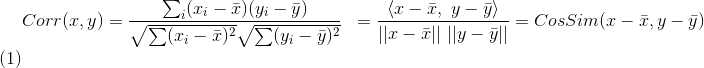
皮爾遜相關係數具有平移不變性和尺度不變性，計算出了兩個向量（維度）的相關性。
在python中的實現：
import numpy as np x=np.random.random(10) y=np.random.random(10) #方法一：根據公式求解 x_=x-np.mean(x) y_=y-np.mean(y) d1=np.dot(x_,y_)/(np.linalg.norm(x_)*np.linalg.norm(y_)) #方法二：根據numpy庫求解 X=np.vstack([x,y]) d2=np.corrcoef(X)[0][1]
相關係數是衡量隨機變數X與Y相關程度的一種方法，相關係數的取值範圍是[-1,1]。相關係數的絕對值越大，則表明X與Y相關度越高。當X與Y線性相關時，相關係數取值為1（正線性相關）或-1（負線性相關）。
9. 漢明距離(Hamming distance)
(1)漢明距離的定義
兩個等長字串s1與s2之間的漢明距離定義為將其中一個變為另外一個所需要作的最小替換次數。例如字串“1111”與“1001”之間的漢明距離為2。
應用：資訊編碼（為了增強容錯性，應使得編碼間的最小漢明距離儘可能大）。
在python中的實現：
import numpy as np from scipy.spatial.distance import pdist x=np.random.random(10)>0.5 y=np.random.random(10)>0.5 x=np.asarray(x,np.int32) y=np.asarray(y,np.int32) #方法一：根據公式求解 d1=np.mean(x!=y) #方法二：根據scipy庫求解 X=np.vstack([x,y]) d2=pdist(X,'hamming')
10. 傑卡德相似係數(Jaccard similarity coefficient)
(1) 傑卡德相似係數
兩個集合A和B的交集元素在A，B的並集中所佔的比例，稱為兩個集合的傑卡德相似係數，用符號J(A,B)表示。
傑卡德相似係數是衡量兩個集合的相似度一種指標。
(2) 傑卡德距離
與傑卡德相似係數相反的概念是傑卡德距離(Jaccard distance)。傑卡德距離可用如下公式表示：
傑卡德距離用兩個集合中不同元素佔所有元素的比例來衡量兩個集合的區分度。
(3) 傑卡德相似係數與傑卡德距離的應用
可將傑卡德相似係數用在衡量樣本的相似度上。
樣本A與樣本B是兩個n維向量，而且所有維度的取值都是0或1。例如：A(0111)和B(1011)。我們將樣本看成是一個集合，1表示集合包含該元素，0表示集合不包含該元素。
在python中的實現：
import numpy as np
from scipy.spatial.distance import pdist
x=np.random.random(10)>0.5
y=np.random.random(10)>0.5
x=np.asarray(x,np.int32)
y=np.asarray(y,np.int32)
#方法一：根據公式求解
up=np.double(np.bitwise_and((x != y),np.bitwise_or(x != 0, y != 0)).sum())
down=np.double(np.bitwise_or(x != 0, y != 0).sum())
d1=(up/down)
#方法二：根據scipy庫求解
X=np.vstack([x,y])
d2=pdist(X,'jaccard')
11. 佈雷柯蒂斯距離(Bray Curtis Distance)
Bray Curtis距離主要用於生態學和環境科學，計算座標之間的距離。該距離取值在[0,1]之間。它也可以用來計算樣本之間的差異。
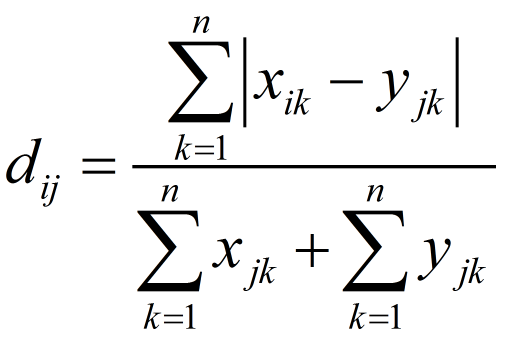
樣本資料：
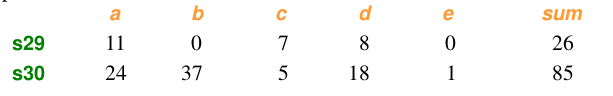
計算：
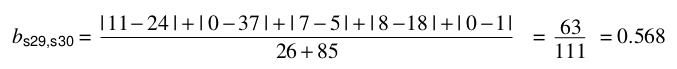
在python中的實現：
import numpy as np
from scipy.spatial.distance import pdist
x=np.array([11,0,7,8,0])
y=np.array([24,37,5,18,1])
#方法一：根據公式求解
up=np.sum(np.abs(y-x))
down=np.sum(x)+np.sum(y)
d1=(up/down)
#方法二：根據scipy庫求解
X=np.vstack([x,y])
d2=pdist(X,'braycurtis')
1、卡方檢驗
統計學上的χ2統計量，由於它最初是由英國統計學家Karl Pearson在1900年首次提出的，因此也稱之為Pearson χ2，其計算公式為
其中，Ai為i水平的觀察頻數，Ei為i水平的期望頻數，n為總頻數，pi為i水平的期望頻率。i水平的期望頻數Ei等於總頻數n×i水平的期望概率pi。當n比較大時，χ2統計量近似服從k-1(計算Ei時用到的引數個數)個自由度的卡方分佈。
卡方檢驗經常用來檢驗某一種觀測分佈是不是符合某一類典型的理論分佈（如二項分佈，正態分佈等)。觀察頻數與期望頻數越接近，兩者之間的差異越小，χ2值越小；如果兩個分佈完全一致，χ2值為0；反之，觀察頻數與期望頻數差別越大，兩者之間的差異越大，χ2值越大。換言之，大的χ2值表明觀察頻數遠離期望頻數，即表明遠離假設。小的χ2值表明觀察頻數接近期望頻數，接近假設。因此，χ2是觀察頻數與期望頻數之間距離的一種度量指標，也是假設成立與否的度量指標。如果χ2值“小”，研究者就傾向於不拒絕H0；如果χ2值大，就傾向於拒絕H0。至於χ2在每個具體研究中究竟要大到什麼程度才能拒絕H0，則要藉助於卡方分佈求出所對應的P值來確定（通常取p=0.05)。
在python中的實現：
# -*- coding: utf-8 -*-
'''
卡方公式(o-e)^2 / e
期望值和收集到資料不能低於5，o(observed)觀察到的資料，e（expected）表示期望的資料
(o-e)平方，最後除以期望的資料e
'''
import numpy as np
from scipy.stats import chisquare
list_observe=np.array([30,14,34,45,57,20])
list_expect=np.array([20,20,30,40,60,30])
#方法一:根據公式求解（最後根據c1的值去查表判斷）
c1=np.sum(np.square(list_observe-list_expect)/list_expect)
#方法二：使用scipy庫來求解
c2,p=chisquare(f_obs=list_observe, f_exp=list_expect)
'''
返回NAN，無窮小
'''
if p>0.05 or p=="nan":
print("H0 win,there is no difference")
else:
print("H1 win,there is difference")
2、交叉熵
通常，一個信源傳送出什麼符號是不確定的，衡量它的不確定性可以根據其出現的概率來度量。概率大，出現機會多，不確定性小；反之就大。
不確定性函式f必須滿足兩個條件：
1）是概率P的單調遞降函式；
2）兩個獨立符號所產生的不確定性應等於各自不確定性之和，即f（P1，P2）=f（P1）+f（P2），這稱為可加性。
同時滿足這兩個條件的函式f是對數函式，即
在信源中，考慮的不是某一單個符號發生的不確定性，而是要考慮這個信源所有可能發生情況的平均不確定性。若信源符號有n種取值：U1…Ui…Un，對應概率為：P1…Pi…Pn，且各種符號的出現彼此獨立。這時，信源的平均不確定性應當為單個符號不確定性-logPi的統計平均值（E），可稱為資訊熵，即
假設現在有一個樣本集中兩個概率分佈p,q，其中p為真實分佈，q為非真實分佈。假如，按照真實分佈p來衡量識別一個樣本所需要的編碼長度的期望為： H(p)= 但是，如果採用錯誤的分佈q來表示來自真實分佈p的平均編碼長度，則應該是： H(p,q)=我們稱H(p)為資訊熵，稱H(p,q)為交叉熵。
交叉熵在CNN分類中經常用到，用來作為預測值和真實標籤值的距離度量。經過卷積操作後，最後一層出來的特徵經過softmax函式後會變成一個概率向量，我們可以看作為是概率分佈q, 而真實標籤我們可以看作是概率分佈p, 因此真實分佈p和預測分佈q的交叉熵就是我們要求的loss損失值，即
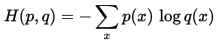
在python中的實現：
import numpy as np
import tensorflow as tf
fea=np.asarray([6.5,4.2,7.4,3.5],np.float32)
label=np.array([1,0,0,0])
#方法一：根據公式求解
def softmax(x):
return np.exp(x)/np.sum(np.exp(x),axis=0)
loss1=-np.sum(label*np.log(softmax(fea)))
#方法二：呼叫tensorflow深度學習框架求解
sess=tf.Session()
logits=tf.Variable(fea)
labels=tf.Variable(label)
sess.run(tf.global_variables_initializer())
loss2=sess.run(tf.losses.softmax_cross_entropy(labels,logits))
sess.close()
3、相對熵(relative entropy)
又稱為KL散度（Kullback–Leibler divergence，簡稱KLD），資訊散度（information divergence），資訊增益（information gain）。
相對熵是交叉熵與資訊熵的差值。即
相對熵=交叉熵-資訊熵
KL(p||q)=H(p,q)-H(p)
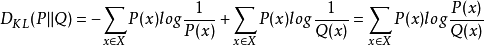
表示用分佈q模擬真實分佈p相比用p模擬p，所需的額外資訊。
相對熵（KL散度）有兩個主要的性質。如下
（1）儘管 KL 散度從直觀上是個度量或距離函式，但它並不是一個真正的度量或者距離，因為它不具有對稱性，即
(2)相對熵具有非負性
總結一下：
資訊熵公式：
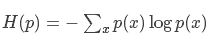
交叉熵公式：
相對熵公式：
三者的關係：
在python中的實現：
import numpy as np import scipy.stats p=np.asarray([0.65,0.25,0.07,0.03]) q=np.array([0.6,0.25,0.1,0.05]) #方法一：根據公式求解 kl1=np.sum(p*np.log(p/q)) #方法二：呼叫scipy包求解 kl2=scipy.stats.entropy(p, q)
4、js散度（Jensen-Shannon）
因為kl散度不具對稱性，因此js散度在kl散度的基礎上進行了改進：
現有兩個分佈p1和p2，其JS散度公式為：
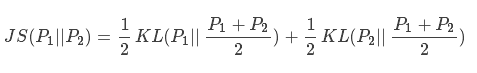
在python中的實現：